3
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Literature on Coordinate Descent
Lots of excellent papers, here are some:
Beck and Tetruashvili, On the convergence of block coordinate descent type
methods
Fercoq and Richtarik, Accelerated, parallel, and proximal coordinate descent
Gurbuzbalaban, Ozdaglar, Parrilo,Vanli, When cyclic coordinate descent
outperforms randomized coordinate descent
Lee and Sidford, Efficient accelerated coordinate descent methods and faster
algorithms for solving linear systems
Lin, Mairal, and Harchaoui, A universal catalyst for first-order optimization
Locatello, Raj, Reddy, R¨atsch, Sch¨olkopf, Stich, Jaggi, On matching pursuit and
coordinate descent
Lu and Xiao, On the complexity analysis of randomized block-coordinate
descent methods
Nesterov, Efficiency of coordinate descent methods on huge-scale optimization
problems
Nutini, Schmidt, Laradji, Friedlander, and Koepke, Coordinate descent
converges faster with the Gauss-Southwell rule than random selection
Richtarik and Takac, Iteration complexity of randomized block-coordinate
descent methods for minimizing a composite function
Wilson, Recht, and Jordan, A Lyapunov analysis of momentum methods in
optimization
5
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Problem of Interest, and Coordinate-wise L-smoothness
P : f
∗
:= minimum
x
f (x)
s.t. x ∈ R
n
where f (·) is a differentiable convex function
Coordinate-wise L-smoothness
f (·) is coordinate-wise L-smooth for the vector of parameters
L := (L
1
, L
2
, . . . , L
n
) if for all x ∈ R
n
and h ∈ R it holds that:
|∇
i
f (x + he
i
) −∇
i
f (x)| ≤ L
i
|h| , i = 1, . . . , n ,
where ∇
i
f (·) denotes the i
th
coordinate of ∇f (·) and e
i
is i
th
unit
coordinate vector, for i = 1, . . . , n.
6
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Coordinate-wise L-smoothness and L notation
Coordinate-wise L-smoothness
f (·) is coordinate-wise L-smooth for the vector of parameters
L := (L
1
, L
2
, . . . , L
n
) if for all x ∈ R
n
and h ∈ R it holds that:
|∇
i
f (x + he
i
) −∇
i
f (x)| ≤ L
i
|h| , i = 1, . . . , n ,
where ∇
i
f (·) denotes the i
th
coordinate of ∇f (·) and e
i
is i
th
unit
coordinate vector, for i = 1, . . . , n.
Define the norm kxk
L
:=
q
P
n
i=1
L
i
x
2
i
and dual norm kvk
L
−1
:=
q
P
n
i=1
L
−1
i
v
2
i
7
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Accelerated Coordinate Descent Framework
Accelerated Coordinate Descent Framework (without Strong Convexity)
Given f (·) with coordinate-wise smoothness parameter L, initial point x
0
and
z
0
:= x
0
. Define step-size parameters θ
i
∈ (0, 1] recursively by θ
0
:= 1 and θ
i+1
satisfies
1
θ
2
i+1
−
1
θ
i+1
=
1
θ
2
i
.
For k = 1, 2, . . ., do:
Define y
k
:= (1 − θ
k
)x
k
+ θ
k
z
k
Choose coordinate j
1
k
(by some rule)
Compute x
k+1
:= y
k
−
1
L
j
1
k
∇
j
1
k
f (y
k
)e
j
1
k
Choose coordinate j
2
k
(by some rule)
Compute z
k+1
:= z
k
−
1
nL
j
2
k
θ
k
∇
j
2
k
f (y
k
)e
j
2
k
.
8
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Accelerated Randomized Coordinate Descent (ARCD)
Accelerated Randomized Coordinate Descent (ARCD) is the specification:
Accelerated Randomized Coordinate Descent (ARCD) (without Strong
Convexity)
Given f (·) with coordinate-wise smoothness parameter L, initial point x
0
and
z
0
:= x
0
. Define step-size parameters θ
i
∈ (0, 1] recursively by θ
0
:= 1 and θ
i+1
satisfies
1
θ
2
i+1
−
1
θ
i+1
=
1
θ
2
i
.
For k = 1, 2, . . ., do:
Define y
k
:= (1 − θ
k
)x
k
+ θ
k
z
k
Choose coordinate j
1
k
by j
1
k
:∼ U[1, ··· , n]
Compute x
k+1
:= y
k
−
1
L
j
1
k
∇
j
1
k
f (y
k
)e
j
1
k
Choose coordinate j
2
k
by j
2
k
= j
1
k
Compute z
k+1
:= z
k
−
1
nL
j
2
k
θ
k
∇
j
2
k
f (y
k
)e
j
2
k
.
9
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
On Accelerated Randomized Coordinate Descent (ARCD)
ARCD is well-studied
ARCD updates 1 coordinate per iteration, hence x
k
is k-sparse
avoids computation of full gradient, which can save computation (or
not) depending on the application
randomization of x -update slows objective function improvement in
practice
Accelerated convergence guarantee (in expectation), for example
[FR2015] :
E
f (x
k
) −f (x
∗
)
≤
2n
2
(k+1)
2
kx
∗
− x
0
k
2
L
,
where the expectation is on the random variables used to define the
first k iterations
10
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Accelerated Greedy Coordinate Descent (AGCD)
Accelerated Greedy Coordinate Descent (AGCD) is the specification:
Accelerated Greedy Coordinate Descent (AGCD) (without Strong Convexity)
Given f (·) with coordinate-wise smoothness parameter L, initial point x
0
and
z
0
:= x
0
. Define step-size parameters θ
i
∈ (0, 1] recursively by θ
0
:= 1 and θ
i+1
satisfies
1
θ
2
i+1
−
1
θ
i+1
=
1
θ
2
i
.
For k = 1, 2, . . ., do:
Define y
k
:= (1 − θ
k
)x
k
+ θ
k
z
k
Choose coordinate j
1
k
by j
1
k
:= arg max
i
1
√
L
i
|∇
i
f (y
k
)|
Compute x
k+1
:= y
k
−
1
L
j
1
k
∇
j
1
k
f (y
k
)e
j
1
k
Choose coordinate j
2
k
by j
2
k
= j
1
k
Compute z
k+1
:= z
k
−
1
nL
j
2
k
θ
k
∇
j
2
k
f (y
k
)e
j
2
k
.
11
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
On Accelerated Greedy Coordinate Descent (AGCD)
AGCD has not been studied in the literature (that we are aware of)
AGCD updates 1 coordinate per iteration, hence x
k
is k-sparse
AGCD computes the full gradient at each iteration, which can be
expensive (or not) depending on the application
the greedy nature of the x-update speeds convergence in practice
no convergence results known for AGCD, in fact we suspect that
there are examples where O(1/k
2
) convergence fails
we observe O(1/k
2
) for AGCD in practice
we will argue (later on) why O(1/k
2
) fails in theory
we will also argue why O(1/k
2
) is observed in practice
13
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Accelerated Semi-greedy Coordinate Descent (ASCD)
Accelerated Semi-greedy Coordinate Descent (ASCD) is the specification:
Accelerated Semi-greedy Coordinate Descent (ASCD) (without Strong
Convexity)
Given f (·) with coordinate-wise smoothness parameter L, initial point x
0
and
z
0
:= x
0
. Define step-size parameters θ
i
∈ (0, 1] recursively by θ
0
:= 1 and θ
i+1
satisfies
1
θ
2
i+1
−
1
θ
i+1
=
1
θ
2
i
.
For k = 1, 2, . . ., do:
Define y
k
:= (1 − θ
k
)x
k
+ θ
k
z
k
Choose coordinate j
1
k
by j
1
k
:= arg max
i
1
√
L
i
|∇
i
f (y
k
)|
Compute x
k+1
:= y
k
−
1
L
j
1
k
∇
j
1
k
f (y
k
)e
j
1
k
Choose coordinate j
2
k
by j
2
k
:∼ U[1, ··· , n]
Compute z
k+1
:= z
k
−
1
nL
j
2
k
θ
k
∇
j
2
k
f (y
k
)e
j
2
k
.
14
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
On Accelerated Semi-greedy Coordinate Descent (ASCD)
ASCD and its complexity analysis is the new theoretical contribution
of this paper
ASCD updates 2 coordinates per iteration, hence x
k
is 2k-sparse
computes the full gradient at each iteration, which can be expensive
(or not) depending on the application
the greedy nature of the x-update speeds convergence in practice
Accelerated convergence guarantee on next slide . . .
15
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Computational Guarantee for Accelerated Semi-greedy
Coordinate Descent (ASCD)
At each iteration k of ASCD the random variable j
2
k
is introduced, and
therefore x
k
depends on the realization of the random variable
ξ
k
:= {j
2
0
, . . . , j
2
k−1
}
Theorem: Convergence Bound for Accelerated Semi-greedy Coordinate
Descent (ASCD)
Consider the Accelerated Semi-Greedy Coordinate Descent algorithm. If
f (·) is coordinate-wise L-smooth, it holds for all k ≥ 1 that:
E
ξ
k
f (x
k
) −f (x
∗
)
≤
n
2
θ
2
k−1
2
kx
∗
− x
0
k
2
L
≤
2n
2
(k+1)
2
kx
∗
− x
0
k
2
L
.
17
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Accelerated Semi-greedy Coordinate Descent (ASCD)
under Strong Convexity
We begin with the definition of strong convexity with respect to k · k
L
due to [LX2015]:
µ-strong convexity with respect to k · k
L
f (·) is µ-strongly convex with respect to k · k
L
if for all x, y ∈ R
n
it holds
that:
f (y) ≥ f (x) + h∇f (x), y − xi +
µ
2
ky − xk
2
L
.
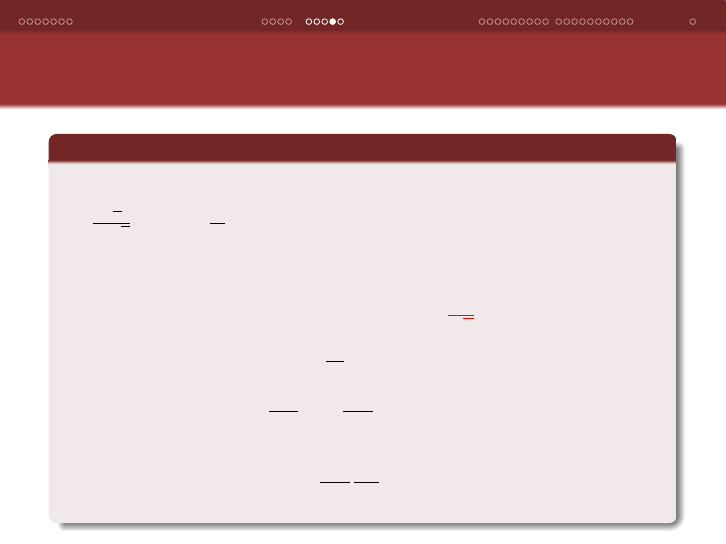
Note that µ can be viewed as an extension of the condition number of
f (·) in the traditional sense since µ is defined relative to the coordinate
smoothness coefficients through k · k
L
18
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Accelerated Coordinate Descent Framework under Strong
Convexity
Accelerated Coordinate Descent Framework (µ-strongly convex case)
Given f (·) with coordinate-wise smoothness parameter L and strong convexity
parameter µ > 0, initial point x
0
and z
0
:= x
0
. Define the parameters
a =
√
µ
n+
√
µ
and b =
µa
n
2
.
For k = 1, 2, . . ., do:
Define y
k
:= (1 − θ
k
)x
k
+ θ
k
z
k
Choose coordinate j
1
k
(by some rule)
Compute x
k+1
:= y
k
−
1
L
j
1
k
∇
j
1
k
f (y
k
)e
j
1
k
Compute u
k
:=
a
2
a
2
+b
z
k
+
b
a
2
+b
y
k
Choose coordinate j
2
k
(by some rule)
Compute z
k+1
= u
k
−
a
a
2
+b
1
nL
j
2
k
∇f
j
2
k
(y
k
)e
j
2
k
.
19
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Accelerated Semi-Greedy Coordinate Descent under Strong
Convexity
Accelerated Semi-greedy Coordinate Descent (µ-strongly convex case)
Given f (·) with coordinate-wise smoothness parameter L and strong convexity
parameter µ > 0, initial point x
0
and z
0
:= x
0
. Define the parameters
a =
√
µ
n+
√
µ
and b =
µa
n
2
.
For k = 1, 2, . . ., do:
Define y
k
:= (1 − θ
k
)x
k
+ θ
k
z
k
Choose coordinate j
1
k
by j
1
k
:= arg max
i
1
√
L
i
|∇
i
f (y
k
)|
Compute x
k+1
:= y
k
−
1
L
j
1
k
∇
j
1
k
f (y
k
)e
j
1
k
Compute u
k
:=
a
2
a
2
+b
z
k
+
b
a
2
+b
y
k
Choose coordinate j
2
k
by j
2
k
:∼ U[1, ··· , n]
Compute z
k+1
= u
k
−
a
a
2
+b
1
nL
j
2
k
∇f
j
2
k
(y
k
)e
j
2
k
.
20
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Computational Guarantee for Accelerated Semi-greedy
Coordinate Descent (ASCD) under Strong Convexity
Theorem: Convergence Bound for Accelerated Semi-greedy Coordinate
Descent (ASCD) under Strong Convexity
Consider the Accelerated Semi-Greedy Coordinate Descent algorithm in
the strongly convex case. If f (·) is coordinate-wise L-smooth and
µ-strongly convex, it holds for all k ≥ 1 that:
E
ξ
k
f (x
k
) − f
∗
+
n
2
2
(a
2
+ b)kz
k
− x
∗
k
2
L
≤
1 −
√
µ
n+
√
µ
k
f (x
0
) − f
∗
+
n
2
2
(a
2
+ b)kx
0
− x
∗
k
2
L
.
In particular, it holds that:
E
ξ
k
f (x
k
) −f
∗
≤
1 −
√
µ
n+
√
µ
k
f (x
0
) −f
∗
+
n
2
2
(a
2
+ b)kx
0
− x
∗
k
2
L
.
Observe that this is an accelerated linear convergence rate ≈ (1 −
√
u/n)
22
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Accelerated Greedy Coordinate Descent (AGCD) (without
Strong Convexity)
Accelerated Greedy Coordinate Descent (AGCD)
Given f (·) with coordinate-wise smoothness parameter L, initial point x
0
and
z
0
:= x
0
. Define step-size parameters θ
i
∈ (0, 1] recursively by θ
0
:= 1 and θ
i+1
satisfies
1
θ
2
i+1
−
1
θ
i+1
=
1
θ
2
i
.
For k = 1, 2, . . ., do:
Define y
k
:= (1 − θ
k
)x
k
+ θ
k
z
k
Choose coordinate j
1
k
by j
1
k
:= arg max
i
1
√
L
i
|∇
i
f (y
k
)|
Compute x
k+1
:= y
k
−
1
L
j
1
k
∇
j
1
k
f (y
k
)e
j
1
k
Choose coordinate j
2
k
by j
2
k
= j
1
k
Compute z
k+1
:= z
k
−
1
nL
j
2
k
θ
k
∇
j
2
k
f (y
k
)e
j
2
k
.
23
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Why AGCD fails (in theory)
In the discrete-time setting, one can construct a Lyapunov energy
function of the form:
E
k
= A
k
(f (x
k
) −f
∗
) +
1
2
kx
∗
− z
k
k
2
L
where A
k
is a parameter sequence with A
k
∼ O(k
2
).
Virtually all proof techniques for acceleration methods can be equivalently
written as showing that E
k
is non-increasing in k, thereby yielding:
f (x
k
) −f
∗
≤
E
k
A
k
≤
E
0
A
k
= O
1/k
2
24
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Why AGCD fails (in theory), continued
E
k
= A
k
(f (x
k
) −f
∗
) +
1
2
kx
∗
− z
k
k
2
L
In AGCD the greedy coordinate j
1
k
is chosen to yield the greatest
guaranteed decrease in f (·).
But one needs to prove a decrease in E
k
, which is not the same as a
decrease in f (·).
The coordinate j
1
k
is not necessarily the greedy coordinate for E
k
due to
the presence of the second term kx
∗
− z
k
k
2
L
.
This explains why the greedy coordinate can fail to decrease E
k
, at least
in theory.
Because x
∗
is not known when running AGCD, there does not seem to be
any way to find the greedy descent coordinate for the energy function E
k
.
25
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Why AGCD fails (in theory), continued
E
k
= A
k
(f (x
k
) −f
∗
) +
1
2
kx
∗
− z
k
k
2
L
In ASCD:
we use the greedy coordinate to perform the x-update (which
corresponds to the best coordinate decrease for f (·))
we choose a random coordinate to perform the z-update (which
corresponds to the second term in the energy function)
This tackles the problem of dealing with the second term of the energy
function.

26
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
A concurrent paper with similar notions: [LRRRSSJ2018]
Locatello, Raj, Reddy, R¨atsch, Sch¨olkopf, Stich, Jaggi, On matching
pursuit and coordinate descent, ICML 2018
Develops computational theory for matching pursuit algorithms, which
can be viewed as a generalized version of greedy coordinate descent
where the directions do not need to be orthogonal
The paper also develops an accelerated version of the matching pursuit
algorithms, which turns out to be equivalent to ASCD when the chosen
directions are orthogonal
Both works use a decoupling of the coordinate update for the {x
k
}
sequence (with a greedy rule) and the {z
k
} sequence (with a randomized
rule)
[LRRRSSJ2018] is consistent with the argument here as to why one
cannot accelerate greedy coordinate descent in general
27
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
How to make AGCD work (in theory)
Consider the following technical condition:
Technical Condition
There exists a positive constant γ and an iteration number K such that
for all k ≥ K it holds that:
1
n
k
X
i=0
1
θ
i
h∇f (y
i
), z
i
− x
∗
i ≤
k
X
i=0
γ
θ
i
∇
j
i
f (y
i
)(z
i
j
i
− x
∗
j
i
) ,
where j
i
= arg max
i
1
√
L
i
|∇
i
f (y
k
)| is the greedy coordinate at iteration i.
We will give some intuition on this in a couple of slides. But first . . .
28
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Computational Guarantee for Accelerated Greedy
Coordinate Descent (AGCD) under the Technical Condition
Theorem: Convergence Bound for Accelerated Greedy Coordinate
Descent (AGCD)
Consider the Accelerated Greedy Coordinate Descent algorithm. If f (·) is
coordinate-wise L-smooth and satisfies the Technical Condition with
constant γ ≤ 1, then it holds for all k ≥ K that:
f (x
k
) −f (x
∗
) ≤
2n
2
γ
(k+1)
2
kx
∗
− x
0
k
2
L
.
(The Technical Condition arises from a reverse engineering of the
structure of the acceleration proof.)
Note that if γ < 1 (which we always observe in practice), then AGCD will
have a better convergence guarantee than ASCD or ARCD.
29
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Why the Technical Condition ought to hold in general
Technical Condition
There exists a positive constant γ and an iteration number K such that for all
k ≥ K it holds that:
1
n
k
X
i=0
1
θ
i
h∇f (y
i
), z
i
− x
∗
i ≤
k
X
i=0
γ
θ
i
∇
j
i
f (y
i
)(z
i
j
i
− x
∗
j
i
) ,
where j
i
= arg max
i
1
√
L
i
|∇
i
f (y
k
)| is the greedy coordinate at iteration i .
The three sequence {x
k
}, {y
k
} and {z
k
} ought to all converge to x
∗
.
Thus we can instead consider the inner product h∇f (y
i
), y
i
− x
∗
i
For any j we have |y
i
j
− x
∗
j
| ≥
1
L
j
|∇
j
f (y
i
)|, and therefore
|∇
j
f (y
i
) ·(y
i
j
− x
∗
j
)| ≥
1
L
j
|∇
j
f (y
i
)|
2
.
The greedy coordinate is chosen by j
i
:= arg max
j
1
L
j
|∇
j
f (y
i
)|
2
It is reasonably likely that in most cases the greedy coordinate will yield a
better product than the average of the components of the inner product.
31
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Numerical Experiments
Linear Regression Problems
least squares minimization: min
β
1
2n
ky − X βk
2
2
synthetic instances in order to control condition number
κ(X
T
X )
n = 200, p = 100
Logistic Regression Problems
logistic loss minimization: min
β
1
n
P
n
i=1
ln(1 + exp(−y
i
β
T
x
i
))
real problem instances taken from LIBSVM
locally strongly convex with parameter µ, we assigned
parameter ¯µ in the experiments
33
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
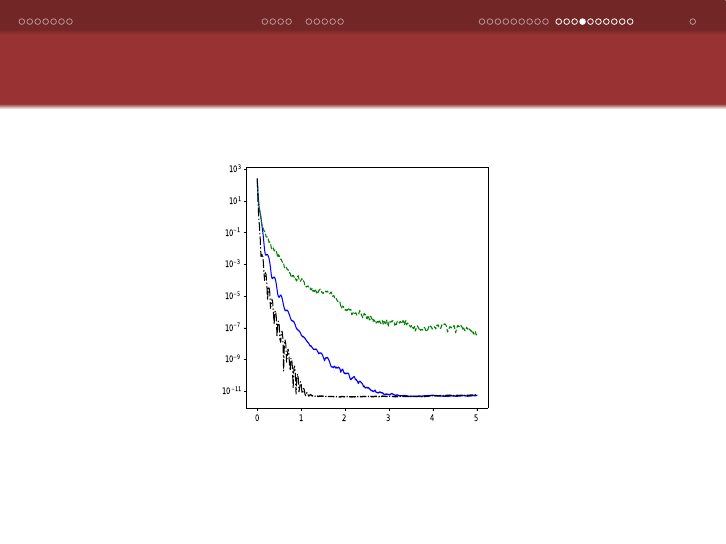
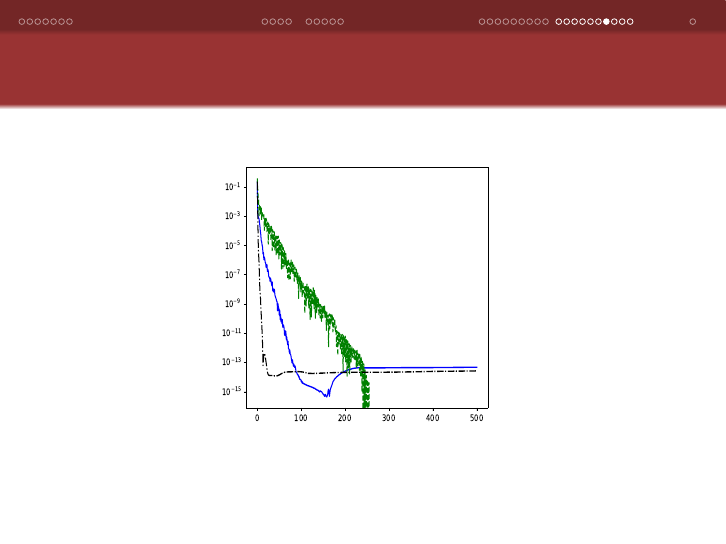
Prototypical Comparison of ARCD, ASCD, and AGCD on
Linear Regression Problems
Figure: Plot showing the optimality gap versus run-time (in seconds) for
a synthetic linear regression instance solved by ARCD, ASCD, AGCD.
34
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
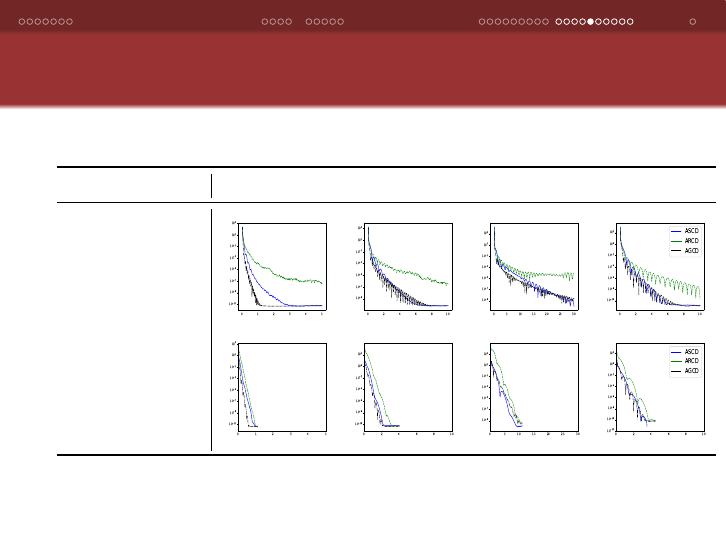
Comparing the Methods on Linear Regression Problems
with Different Conditions Numbers κ(X
T
X )
κ = 10
2
κ = 10
3
κ = 10
4
κ = ∞
Algorithm
Framework 1
(non-strongly
convex)
Algorithm
Framework 2
(strongly
convex)
Plots showing the optimality gap versus run-time (in seconds) for
synthetic linear regression problems solved by ARCD, ASCD, AGCD.
36
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Prototypical Comparison of ARCD, ASCD, and AGCD on
Logistic Regression Problems
Figure: Plot showing the optimality gap versus run-time (in seconds) for
the logistic regression instance a1a solved by ARCD, ASCD, AGCD.
37
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
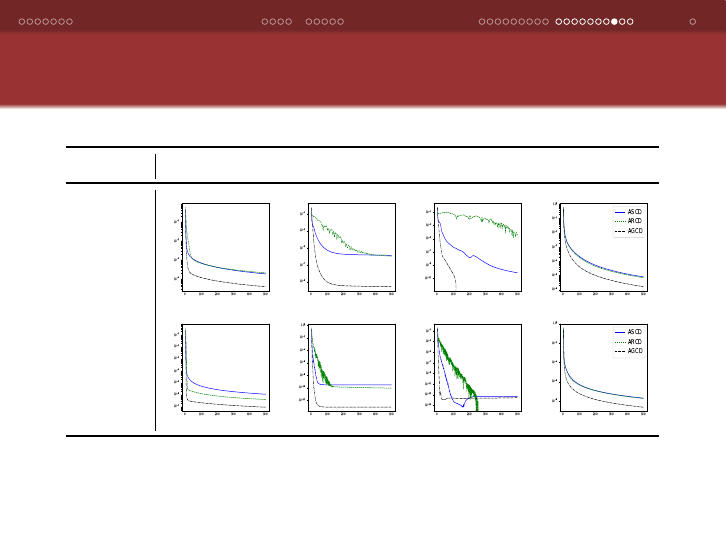
Comparing the Methods on Logistic Regression Problems
with Different Assigned Strong Convexity Parameters ¯µ
Dataset
¯µ = 10
−3
¯µ = 10
−5
¯µ = 10
−7
¯µ = 0
w1a
a1a
Plots showing the optimality gap versus run-time (in seconds) for the
logistic regression instances w1a and a1a in LIBSVM, solved by ARCD,
ASCD, AGCD.
38
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Empirical Values of γ arising from the Technical Condition
Dataset γ
w1a 0.25
a1a 0.17
heart 0.413
madelon 0.24
rcv1 0.016
Largest observed values of γ for five different datasets in LIBSVM for
k ≥
¯
K := 5000.
39
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Comparing the Algorithms using Running Time and the
Number of Iterations
Plots showing the optimality gap versus run-time (in seconds) on the left
and versus the number of iterations on the right, for the logistic
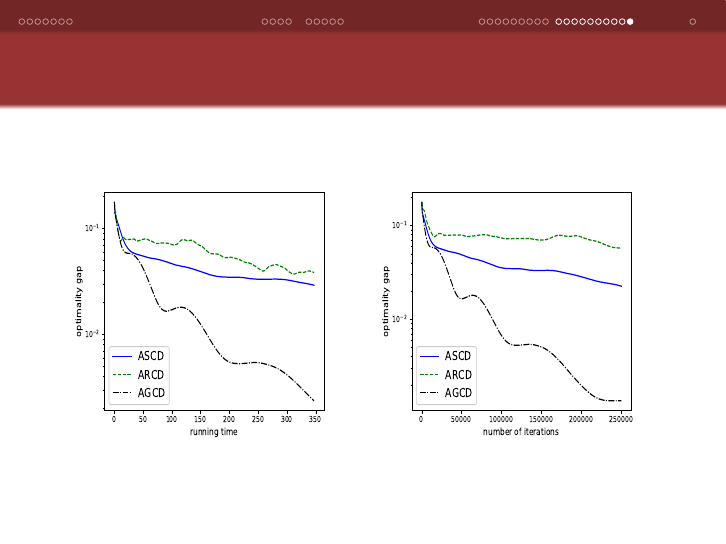
regression instance madelon, solved by ARCD, ASCD, AGCD.
40
Accelerated Coordinate Descent Framework ASCD ASCD under Strong Convexity AGCD Numerical Experiments End
Conclusions/Remarks
AGCD:
the natural accelerated version of Greedy Coordinate Descent
unlikely that AGCD has an acceleration guarantee (O(1/k
2
))
exhibits acceleration in practice
extremely effective in practice
Technical Condition “explains” acceleration in practice
ASCD:
new theoretical contribution of this paper
combines salient features of AGCD and ARCD
acceleration guarantee (O(1/k
2
))
accelerated linear convergence with rate ≈ (1 −
√
µ/n) in strongly convex
case
very effective in practice
We thank Martin Jaggi as well as three excellent anonymous referees