This is page i
Printer: Opaque
t
Solution M anual
G am e T heory: A n In trodu ction
Steve Tadelis
Jan uary 31, 2013
Th is is page ii
Printer: Opaque
t
ABSTRACT This Slution Manual is incomplete. It will be updated every 2-3 weeks
to add the solutions to problems as they become available. A complete version is
expected by March 15, 2013.
Th is is page iii
Printer: Opaque
t
C on ten ts
I R a tio n a l De c isio n Mak in g 2
1 The Single-P erson Decision Problem 3
2 Introducing Uncertain ty and T ime 13
II Static G ames of Complete Information 44
3Preliminaries 45
4 R a tio n a lity and Com mon Knowledge 51
5 P in n in g Down Beliefs: Nash Equ ilibrium 61
6 Mixed Strategies 95
Contents 1
III Dynamic Games of Complete Information 113
7 Preliminaries 115
8 Credibility and Sequen tial Rationalit y 133
9 M ulti-Stage Games 163
10 Repeated G am es 179
11 Strategic B argaining 197
IV Static Gam es of Incomplete Information 206
12 Ba yesian Game s 207
13 Auctions and Com petitiv e Bidding 215
14 Mechanism Design 221
V Dynamic Gam es of Incomplete Information 222
15 Sequen tial Rationalit y with Incomplete Information 223
16 Signaling Games 231
17 Building a Reputation 239
18 Information Transm ission and Cheap Talk 243
Part I
R ational De cision M aking
2
This is page 3
Printer: Opaque
t
1
The Single-P erson D ecision P roblem
1. Think of a simple decision y ou face regularly and formalize it as a decision
problem , carefully listing the actions and outcomes withou t the preference
relation. Then, assign payoffs to the outcom es, and dra w the decision tree.
2. Going to the Movies: There are two movie theatres in you r neighbor-
hood: Cineclass, which is located one mile from yo ur home, and Cineblast,
located 3 miles from you r home, eac h showing three films.Cineclassisshow-
ing Casablanca, Gone with the Wind and Dr. Str angelove, while Cineblast
is show ing The Matrix, Blade Runner and Aliens. Your problem is to decide
which movie to go to.
(a) Dra w a decision tree tha t represents this problem without assigning
pa y off values.
Answ er:

4 1. The Single-Person Decision Problem
¥
(b) Imagine that you don’t care about distance and that y our preferences
for movies is alphabetic (i.e., y ou like Aliens the most and The Matrix
the least.) U sin g payoff values 1 throug h 6 complete th e decision tree
y ou drew in part (a). What option wou ld y ou choose?
Answ er:
¥
(c) Now ima gin e tha t you r car is in the shop , and the cost of walk in g each
mile is equal to one unit of pay off.Updatethepayoffs in the decision
tree. Would y our c hoice change?
Answ er:
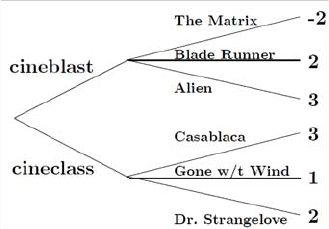
1. The Single-Person Decision Problem 5
¥
3. Fruit or Candy: A banana costs $050 and a candy costs $025 at the local
cafeteria. You have $1.25 in your pocket and y ou value money. The money-
equivalent value (payoff) you get from eating y our first banana is $1.20, and
that of each additiona l banana is half the previous one (the second banana
gives y ou a value of $0.60, the third 0.30, etc.). Similarly, the pa y off you get
from eating your first candy is $0.40, and that of eac h additional candy is
half the previous one ($0.20, 0.10, etc.). Your value from eating bananas is
not affected by ho w ma ny candies you eat and vice v ersa.
(a) What is the set of possible actions you can tak e given your budget of
$1.25?
Answ er: You can buy any combination of bananas and candies that
sum up to no more than $1.25. If we denote by ( ) the choice to buy
bananas and cand ies, then the set of possible actions is
= {(0 0) (0 1) (0 2) (0 3) (0 4) (0 5) (1 0) (1 1) (1 2) (1 3) (2 0) (2 1)}
¥
(b) Dra w the decision tree that is associated with this decision problem.
Answ er: For each c hoice you need to calculate the final net value. For
example, if y ou buy one banana and 2 candies then y ou get 1.2 w orth
from the banana, 0.4 from the first candy an d 0.2 from the second which
totals 1.8. To this w e need to add the $0.25 you ha ve left (the cost was
only $1) so the net final v alue you hav e is 2.05.
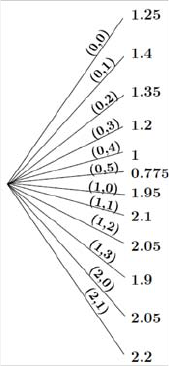
6 1. The Single-Person Decision Problem
¥
(c) Should you spend all yo ur money at the cafeteria? Justify y our answ er
with a rational choice argum en t.
Answ er: Yes. The highest net final value if from buying two bananas
and one candy. ¥
(d) No w imagine that the price of a candy increased to $030.Howmany
possible actions do you have? Does your answer to (c) above chan ge?
Answ er: Of the 12 options above, three are no longer possible: (0 5) (1 3)
and (2 1).Also,thenetfinal values change because each candy is 5
cen ts more expensive. The highest net final value is 2.05 whic h can be
obtained from one of two choices: (1 1) and (2 0), both lea ving some
money in the decision maker’s poc ket. ¥
4. Alcohol Consumption: Recall the examp le in which you needed to choose
ho w m uc h to drink. Imagine that your payoff function is given by − 4
2
,
where is a parameter that depends on yo ur ph ysique. Ev ery person m ay
ha v e a different value of , and it is known that in th e population ()the
smallest is 02;() the largest is 6;and()largerpeoplehavehigher’s
than smaller people.
1. The Single-Person Decision Problem 7
(a) Can you find an am ount of drinking that no person should drink?
Answ er: The utilit y from drinkin g 0 is equal to 0. If a decision maker
drinks =2then, if he has the largest =6,hispayoff is =6× 2 −
4 × (2)
2
= −4 and it is easy to see th at decision m akers w ith smaller
values of will obtain an even more negativ e payoff from consuming
=2. Hence, no person should choose =2. ¥
(b) How much should y ou drink if yo u r =1?If =4?
Answ er: The optimal solu t i on is ob t ained b y maxi mizing the p ay off
function ()= − 4
2
.Thefir st-order maximization condition is
− 8 =0implyin g that =
8
is the optimal solution. For =1the
solution is =
1
8
and for =4it is =
1
2
. ¥
(c) Sho w tha t in general, smaller people should drink less than larger people.
Answ er: This fo llows from the so lution in part (b) a bo ve. For ev e ry
type of person , the solution is ()=
8
which is increasing in ,and
larger people ha ve higher values of ¥
(d) Should an y person drink more than one bottle of wine?
Answ er: N o. Ev en the largest type of person with =6should only
consume =
3
4
of a bottle of wine. ¥
5. Buying a Car: Youplanonbuyingausedcar.Youhave$12,000,andyou
arenoteligibleforanyloans.Thepricesofavailablecarsonthelotaregiven
as follo ws:
Make, Model & Year Price
To yota Corolla 2002 $9,350
Toyota Camry 2001 $10,500
Buick LeSabre 2001 $8,825
Honda Civic 2000 $9,215
Subaru Impreza 2000 $9,690
For any given year, you prefer a Ca m ry to an Impreza , an Im preza to a
Corolla, a Corolla to a Civic and a Civic to a LeSabre. For any given ye ar,
8 1. The Single-Person Decision Problem
you are willing to pay up to $999 to move form a car to the next preferred
car. For example, if the price of a Corolla is $, then you are willing to buy
it over a Civic if the Civic costs mo r e that $( − 999) but you w ould prefer
buy ing the Civic if it costs less than this amo u nt. Similarly, you prefer the
Civic at $ to a Corolla that costs more than $( + 1000) but y ou prefer the
Corolla if it costs less. For any given c ar,youarewillingtomovetoamodel
a year older if it is chea per b y at least $500 For example, if the price of a
2003 Civic is $, then you are willing to buy it o ver a 200 2 Civic if the 2002
Civic costs more that $( −500) but you would prefer buying the 2002 Civic
ifitcostslessthanthisamount.
(a) What is y our set of possible alternatives?
Answ er: Given that you have $12,000, w hich is m ore than the price
of any car, y ou have six alternativ es: any one of the five cars or buying
nothing. ¥
(b) Whatisyourpreferencerelationbetweenthealternativesin(a)above?
Answ er: To answer this we need use the information on willingness to
pay giv en in the question, together with the prices. The least valued
car w ould be a 2000 LeSabre. Assum e that the value of ow ning that car
is given by . From the information above, a 2000 Civic is valued at
+999, a 2000 Corolla is valued at +1 998,andsoonuptoa2000
Camry valued at +3 996. Similarly, eac h of these ca rs for the year
2001 is valued at 500 m ore than the 2000 model, and the 20 02 model
is valued at 1,000 more than the 2000 model. Hence, w e can write the
tableofvaluesasfollows:
Make and Model year 2000 y ear 2001 year 2002
Toyota Camry +3 996 +4 496 +4 996
Subaru Impreza +2 997 +3 497 +3 997
Toyota Corolla
+1 998 +2 498 +2 998
Hond a Civic +999 +1 499 +1 999
Buick LeSabre +0 +500 +1 000
1. The Single-Person Decision Problem 9
Now, to see what the net value from eac h purchase would be w e must
deduct the price of the car from the value. Using the five prices given
aboveandthevalueswejustcalculatedwehavenetpayoffsas(e.g.,for
the 2002 Corolla, the net pa yoff is +2 998 − 9 350 = − 6 352),
Make, Model & Year Price
Toyota Corolla 2002 − 6 352
Toyota Camry 2001 − 6 004
Buick LeSabre 2001 − 8 325
Honda Civic 2000 − 8 216
Subaru Impreza 2000 − 6 693
Assum ing that is large enough to wan t to buy any car, the ranking
of the alternativ es is, Toyota Camry 2001, followed b y To yota Corolla
2002, followed by Subaru Impreza 2000, followed by Honda Civic 2000
and last being the Buic k LeSab re 2001. ¥
(c) Dra w a decision tree an assign payoffs to the terminal nodes associated
with the possible alternativ es. Wh at would y o u c h oose?
Answ er: This follow s directly from th e analy sis in (b) abo ve: you shou ld
c hoose the Toyota Camry 2001 (with six branches, including no pur-
chase.) ¥
(d) Can you dra w a decision tree with different pa yoffs that represents the
same pro blem ?
Answ er: Because w e left as undetermined, w e can find many v alues
of that will represen t this problem. Notice that if is small enough
(less than 6,004) then the best choice w o uld be not to buy a car. ¥
6. Fruit Trees: You h ave room for up to t wo fruit bearing trees in your gar de n.
The fruit trees that can grow in y our garden are either apple, orange or pear.
The cost of maintenance is $100 for an ap ple tree, $70 for an orange tree and
$120 for a pear tree. Your food bill w ill be reduced b y $130 for each apple
tree you plant, b y $145 for each pear tree you plan t and b y $90 for eac h

10 1. The Single-Person Decision Problem
orange tree you plant. You care only about your total expenditure in makin g
any planting decisions.
(a) What is the set of possible actions and related outcomes?
Answ er: Youhavetwo“slots”thatcanbeleftempty,orhaveoneof3
possible trees plan ted in eac h slot. Hence, you have 10 possible c h oices.
1
Theoutcomeswilljustbethechoicesofwhattoplant.¥
(b) What is the pa yoff of eac h action/outcome?
Answ er: To calculate the pay offsfromeachchoiceitisconvenientto
useatableasfollows:
Choice cost food sa vings net pa yoff
nothing 00 0
one apple tree 100 130 30
one orange tree 70 90 20
one pear tree 120 145 25
t wo ap ple trees 200 260 60
t wo orange trees 140 180 40
t wo pear trees 240 290 50
apple and orange 170 220 50
apple and pear 220 275 55
pear and orange 190 235 45
(c) Which actions are dom ina ted?
Answ er: All but choosing t wo apple trees are dominated. ¥
(d) Dra w the associated decision tree. What will a rational play er choose?
Answ er: Thetreewillhavetenbrancheswiththepayoffs associated
with the table abo ve, and the optim al c ho ice is two apple trees. ¥
1
Th is is a pro be m o f cho o sing 2 items out of 4 poss ib i litie s wit h rep la ce ment, wh ich i s equ a l to
4+2−1
2
=
(4+2−1)!
2!(4−1)!
=
5×4
2
=10.
1. The Single-Person Decision Problem 11
(e) Nowimaginethatthefoodbillreductionishalfforthesecondtreeof
thesamekind(youlikevariety).Thatis,thefirst apple still reduces
y o u r food bill by $130, but if y o u plan t t wo apple trees y o u r food bill
will be reduced b y $130 + $65 = $195. (Similarly for pear and orange
trees.) What will a rational player choose now?
Answ er: An ap ple tree is still the best ch oice for the first tree, but no w
thesecondtreeshouldbeapeartree.¥
7. City P arks: A city’s mayor has to decide how much money to spend on
parks and recreation. City codes restrict this spending to be no more than
5% of the budget, and the yearly budget of the city is $20,000,0 00. He wants
to please his constituen ts who ha v e diminishing returns from parks. The
money-equivalen t benefitfromspending$ on parks is ()=
√
400 −
1
80
.
(a) What is the action set of the city’s mayor?
Answ er: The lim it on spendin g is $1 million, so the actions set is
∈ [0 1000000]. ¥
(b) Ho w m uch should the mayor spend?
Answ er: The maximizat ion prob lem is
max
∈[01000000]
√
400 −
1
80
and taking the der ivativ e for the first-order condition we obtain,
10
√
−
1
80
=0,
or =$640 000. T he second order d erivative is −5
−
3
2
0 so this is
indeed a maximum. ¥
(c) The mo vie A n Inc onvenient Truth has shifted public opinion and no w
people are mor e willing to pay for parks. The new pr eferences of the
people are giv en by ()=
√
1600 −
1
80
.Whatnowistheactionset

12 1. The Single-Person Decision Problem
of the ma yor, and ho w much spending should he choose to cater to his
constituents?
Answ er: The first-ord er condition is now,
20
√
−
1
80
=0,
or =$2 560 000. This exceeds the budget and hence the optim al
solution is to spend $1 million. ¥

This is page 13
Printer: Opaque
t
2
Introdu cing U ncerta in t y a nd T im e
1. Getting an MB A : Recall the decision problem in Section 2.3.1, and now
assum e that the probabilit y of a strong labor market is ,ofanaveragelabor
marketis0.5andofaweaklabormarketis05 −. All the other values are
the same.
(a) For which values of willyoudecidenottogetanMBA?
Answ er: The expected pay offsfromeachchoicearegivenby,
(Get MBA)= × 22 + 05 × 6+(05 − ) × 2=20 +4
(Don’t get MBA)= × 12 + 05 × 8+(05 − ) × 4=8 +6
which imp lies that getting an MBA is worthw hile if and only if
20 +4≥ 8 +6
or, ≥
1
6
¥
(b) If =04, what is the highest price the univ ersity can charge for you
to be willing to go ahead and get an MB A ?
14 2. Introducing Uncertainty and Time
Answ er: If =04 then the pa yoffsare,
(Get MBA)=04 × 22 + 05 × 6+01 × 2=12
(Don’t get MBA)=04 × 12 + 05 × 8+01 × 4=92
which implies that an extra charge of up to 2.8 can be c h arged by the
university and y ou wo uld still be willing to get an MB A . ¥
2. Recreation Ch oices: A player has three possible ven ues to c hoose from:
going to a football game, going to a bo xing mat ch, or going for a hik e.
The pay off from each of these alternatives will depend on the weather. Th e
following table gives the agent’s pa yoff in eac h of the two re levant w ea ther
ev ents:
Alternative pay off if R ain payoff if Shine
Football game 1 2
Bo xing Match 3 0
Hike 0 1
For Let denote the probability of rain.
(a) Is there an alternative that a rational pla yer will nev e r take regardless
of ? (i.e., it is dom ina ted for any ∈ [0 1].)
Answ er: For this decision maker c hoosing the hike is always w orse
(dominated) by going to the football game, and he should never go on
ahike.¥
(b) What is the optima l decision, or best response, as a function of .
Answ er: The expected payoffs from eac h of the remain ing two c h oices
are giv en by,
(Football)= × 1+(1− ) × 2=2−
(Boxing)= × 3+(1− ) × 0=3
which implies that football is a better choic e if and only if
2 − ≥ 3
2. Introducing Uncertainty and Time 15
or, ≤
1
2
, and boxin g is better otherwise. ¥
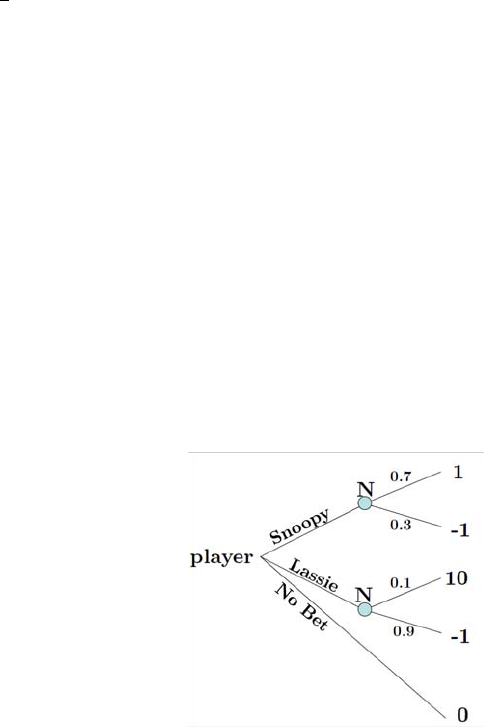
3. At the Dog Races: You’re in Las Vegas, and you can decide what to do at
the dog-racing bet room. You can c hoose not to participate, or you bet on
one of t wo dogs as follo w s. Betting on Snoopy costs $1, and y ou will be paid
$2 if he wins. Betting on Lassie costs $1, and you will be paid $11 if she wins.
You believe that Snoop y has probab ility 0.7 of winnin g and that Lassie has
proba bility 0.1 of winn ing (there are other dogs that you are not considerin g
betting on). Your goal is to maximize the expected monetary return of your
action.
(a) Dra w the decision tree of this problem.
Answ er:
(b) What is your best course of action, and wh at is your expected value?
Answ er: The expected payoff from betting on Snoopy is 07−03=04
while betting on Lassie yields 1 −09=01, so betting on Snoop y is the
best action. ¥
(c) Someone com es an d offersyougambler’santi-insurancetowhichyou
can agree or not. If you agree to it, you get paid $2 up front and y ou
agree to pa y back 50% of any winnings you receive. Draw the new de-
cision tree, and find the optimal action.
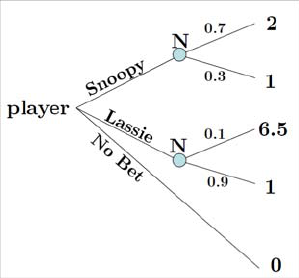
16 2. Introducing Uncertainty and Time
Answ er:
The best action is still to bet on Snoopy with an expected payoff of 1.7
v e rsu s 1.55 from betting on Lassie. ¥
4. Dr illin g for Oil: An oil dr illing com p any m u st decide whether or not t o
engag e in a new drilling activit y before regulators pass a la w tha t bans drillin g
at that site. The cost of drilling is $1,000,000. After drilling is complet ed and
the drilling costs are incurred, then the com pa ny will learn if there is oil or
not. If there is oil, operating profits generated are estimated at $4,000,000.
If there is no oil, there will be no future profits.
(a) Using to denot e the likelihood that drilling results in oil, dra w th e
decision tree of this problem.
Answ er: Two decision br a nches: drill or n ot drill. Following drilling,
Nature c hooses oil with probabilit y ,withthepayoff of $3 million (4
minus the initial investment). With p rob ab ility 1 − Nature ch ooses
no-oil with a pa y off $ − 1 million. ¥
(b) The company estima tes that =06. What is the expected value of
drilling? Sho u ld the comp any go ahead and drill?
Answ er: The expected pa yoff (in millio ns ) from drilling is × 3 −(1 −
) × 1=4 − 1=06, which means that the company should drill. ¥
(c) To be on the safe side, the company hires a specialist to come up with a
more accurate estimate of . What is the minimum vale of for wh ich

2. Introducing Uncertainty and Time 17
it w ou ld be the company’s best response to go ahead and drill?
Answ er: Th e minimum value of for whic h drilling causes no expected
loss is calculate d by solving × 3 − (1 − ) × 1 ≥ 0,or ≥
1
4
¥
5. Discount Prices: A local department store puts out products at an initial
price, and ev ery week the product goes unsold, its price is discoun ted by
25% of the origin al pr ice. If it is not sold a fte r 4 w ee ks, it is sent bac k t o
the r egiona l wa rehou se. There is a set of bu tcher kniv es that was just put
out for the price of $200. Your willingness to pa y for the knives (your dollar
value) is $180, so if you buy them at a price ,yourpayoff is =180− .
If you don’t buy the knives, the c han ces that they are sold to someo ne else
conditio nal on not selling in the week before are giv en in the follo w in g table:
week 1 0.2
week 2 0.4
week 3 0.6
week 4 0.8
For example, if y ou do not buy it during the first t wo weeks, the likelihood
that it is a vailable at the beginning of the third w eek is the likelih ood that
it does not sell in either weeks 1 and 2, which is 08 × 06=048.
(a) Drawyourdecisiontreeforthe4weeksaftertheknivesareputoutfor
sale.
Answ er: We can draw each week as having nature mo ve first to deter-
mine whether someone else bought the kniv es, and if they did not, then
our pla yer can buy or w ait. The tree therefore will be,
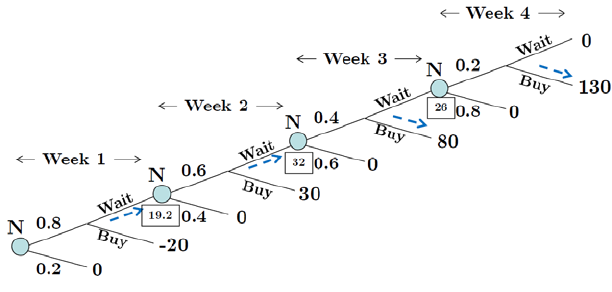
18 2. Introducing Uncertainty and Time
where the numbers in the squares next to Nature’s nodes mark the ex-
pected value from c h oosing w ait before tha t node. ¥
(b) A t the beginning of which w eek, if any, should you run to buy the
knives?
Answ er: We solve this bac kward. In week 4 the player will buy the
knives of they are there. Waiting in w eek 3 gives an expected payoff
of only 02 × (180 − 50) = 26, while buying in w eek 3 gives a pa yoff of
180−100 = 80 26, so buying in w eek 3 beats wa iting. Moving back to
week 2, waiting giv es an expected payoff of 04 × 80 = 32 while buying
yields 180−150 = 30 32 so waiting beats buying, and moving back to
w eek 1 mak es waiting ev en more valuable compared to buying (buying
in w e e k 1 is dominated by not bu y ing. Hence, the player will wai t till
week 3 and then try to buy the kniv e s. ¥
(c) Find a willingn ess to pay for the knives tha t w o u ld make it optim al to
buy at the beginning of the first week.
Answ er: Waiting is risky so intuitively, to make an early p u rchase
valuable, the willingn ess to pay must be very high. Set the willingness
to pa y at 1000. In week 4 the pla yer will buy the kniv es. Waiting in w eek
3yields02 × (1000 − 50) = 190, while buying in week 3 give s a payoff
of 1000 − 100 = 900 190, so buying in w eek 3 beats w aiting. Mo ving
back to w eek 2, waiting gives an expected payoff of 04×190 = 76 while
buying yields 1000 − 150 = 850 76 so buying beats w aiting. Moving

2. Introducing Uncertainty and Time 19
back to week 1, w aiting gives an expected pa yoff of 06 × 850 = 510
wh ile buying yields 1000 −200 = 800 510 so buying in the first w eek
is the optim a l decision. ¥
(d) Find a willingn ess to pay that would make it optima l to buy at the
beginning of the fourth w eek.
Answ er: Similarlyto(c)above,tomakealatepurchasevaluable,the
willing nes s to pay m ust be quite lo w. Set the willingn ess to pa y at 100.
In any wee k but we ek 4 the price is above the willingne ss to pay, so the
optim al decision is to wait for we ek 4 and then buy the kniv es if they
are a vailable. ¥
6. Real Estate Developm ent: A real estate dev eloper wishes to build a new
dev elopment. Regulations impose an en vironmen tal impact study that will
yield an “imp act score,” whic h is an index n umber based on the impact the
developm e nt will likely have on traffic, air qualit y, sew age and water usage,
etc. The developer, w ho has lots of experience, knows that the score will
be no less than 40, and no m ore than 70. Furthermore, he knows th at any
score between 40 and 70 is as likely as any other score bet ween 40 and 70
(use continuous values ). The local go vernment’s past behavior implies that
there is a 35% chance that it will approve the development if the impact
score is less than 50, a 5% chance that it will approve the dev elopmen t if
the score is bet ween 50 and 55, and if the score is greater than 55 then the
project will surely be halted. The v alue of the developmen t to the devel-
oper is $20,000,000. Assuming that the developer is risk neutral, what is the
maxim u m cost of the impact study suc h that it is still w orth while for the
dev eloper to have it conducted?
Answ er: Observ e that there is a
1
3
probability of getting a score between
40 and 50 giv en that 40 to 50 is one-th ird of the range 40 to 70. There is
a
1
6
proba bility of getting a score bet ween 50 and 55 giv en that 50 to 55 is
one-sixth of the range 40 to 70. Hence, the expected value of doing a study

20 2. Introducing Uncertainty and Time
is
1
3
× 35 × $20 000 000 +
1
6
× 05 × $20 000 000 +
1
2
× 0 × $20 000 000
=$2 500 000
Hence, the most the dev eloper should pa y for the study is $2,500,000. ¥
7. Toys: WakTek is a renowned man ufactu rer of electronic to ys, with a spe-
cialty in r emote-controlle d (RC) miniature vehicles. WakTek is consid erin g
the introduction of a new product, an R C Ho vercraft called WakA tak. Pre-
liminary designs ha v e already been produced at a cost of $2 million. To
introduce a marketable product requires the building of a dedicated product
lineatacostof$12 million. Also, before the product can be launc hed a pro-
tot y pe need s to be built and tested for safety. The prototy pe can be crafted
ev en in the absence of a production line, at a cost of $05 million, but if the
prototype is built after the production line then its cost is negligible.
1
There
is uncertaint y over what safety rating WakAtak will get. This could have a
large impact on demand, as a lower safet y-rating will increase the minimum
age required from users. The safety-testing costs $1 million. The outcome of
the safet y-test is estimated to ha ve a 65% c h ance of resulting in a minimum
age of 8 years, a 30% c han ce of m inimum age 15 years, and a 5% chance of
being declared unsafe in whic h case it could not be sold at all. (The cost of
improving the safety status of a finished design is deem ed prohibitive.) Af-
ter successful safety-testing the product could be launched at a cost of $15
million .
There is also uncertaint y o ver demand, which will have a crucial impact on
the ev entual profits. Currently the best estimate is that the finished product,
if available to the 8 − 14 demographic, has a 50 − 50 c han ce of resulting in
profits of either $10 million or $5 million from that demographic. Similarly
there is a 50−50 ch ance of either $14 million or $6 million profitfromthe15-
or-above demo grap hic. These dem an d outcom e s are independent across the
demographics. The profits do not take into account the costs defined abo v e;
1
“Negligible” mean s you can treat it as zero.
2. Introducing Uncertainty and Time 21
they are measured in expected present-value terms so they are directly com-
parable with the costs.
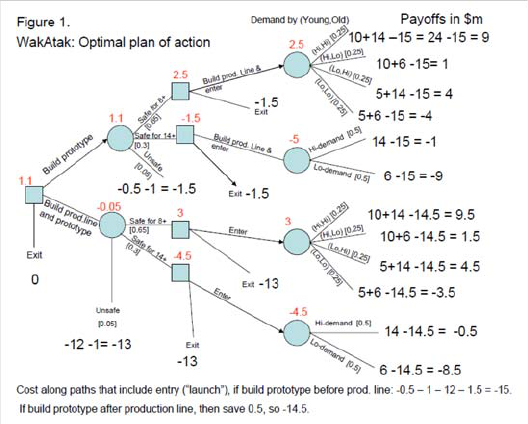
(a) What is the optimal plan of actio n for WakTek? W ha t is currently the
expected economic value of the WakAtak project?
Answ er: The optim al plan is to build the prototype first and then do
the safety test, then build the production line and launch the product
only if the safet y test results in the “safe for 8 years and above” status.
The expected economic profits from this plan are $1.1 million. For jus-
tification of this answer, consider the follow ing decision tree:
Notice that the cost of the prelim inar y design is sunk (cannot be recov-
ered) and should be ignored. ¥
(b) Suddenly it turns out that the original estimate of the cost of safet y-
testing w as incorrect. Analyze the sensitivit y of WakTek’s optima l plan
of action to the cost of safet y-testing.
Answ er: If the cost of safety-testing is too high, then the expected
value becomes negativ e and the optimal plan is to exit the project. To
find out the threshold cost of safety-testing abov e which exit becomes
optim al, notice that the cost of safet y-testing is incurred for sure under

22 2. Introducing Uncertainty and Time
the optimal plan of action which brings expected profits of $1.1 million.
Therefor e, if the cost of safety-testing is increased by $1.1 million or
more (bringing it to $2.1 million or more) then the decision should be
c hanged to “exit.” ¥
(c) Suppose WakTek has also the possibility of conducting a market surv ey,
which would tell exactly wh ich dem and scenario is true. This m a rket
researc h costs $15 million if done simu ltaneo usly for both demograph -
ics, and $1 million if done for one demogr ap hic only. How, if at all, is
theanswertoparta)affected?
Answ er: Firstexaminethedecisiontreefromparta)toseewhether
we can simplify the effect of the market research, b y elimina ting som e
logically possible alternativ e s. Which alternatives to eliminate from the
tree as “ob viously irrelevan t” is partly a matter of taste. For example,
there are poin ts in the tree where the opportunit y to exit is irrelevan t
(e.g.afterwe’vefoundoutthatdemandishighforthe“young”
2
)be-
cause the profits will clearly be higher by not exiting. You can alwa ys
just include all alternativ e s, although that can lead to a v ery large tree;
the final answer is of course unaffected. Elim inations that are not obvi-
ous but that were used in simplifying the decision trees are justified b y
logic as follow s:
(i) We can com plet ely ignore the possibility of building a production line
before the safety test. We already established in part (a) that doing the
safety test first achiev es expected profits that are (11−(−005) = 115)
million higher than doing the production line first. The only poten tial
benefitofdoingtheproductionlinefirst is the sa ved $0.5 million pr o-
totype cost. Thus no information could ever c hange the differ ence in
pa y offs to the advantage of a “production line first” plan b y more than
this $0.5 million. Since research always costs at least $1 million, “prod.
line first” can not become optim al due to the possibilit y of doing market
2
For b revity, th e 8-14 dem og raphic is henceforth referred to as the “young,” and th e 14+ dem ograp hic as the
“old.”
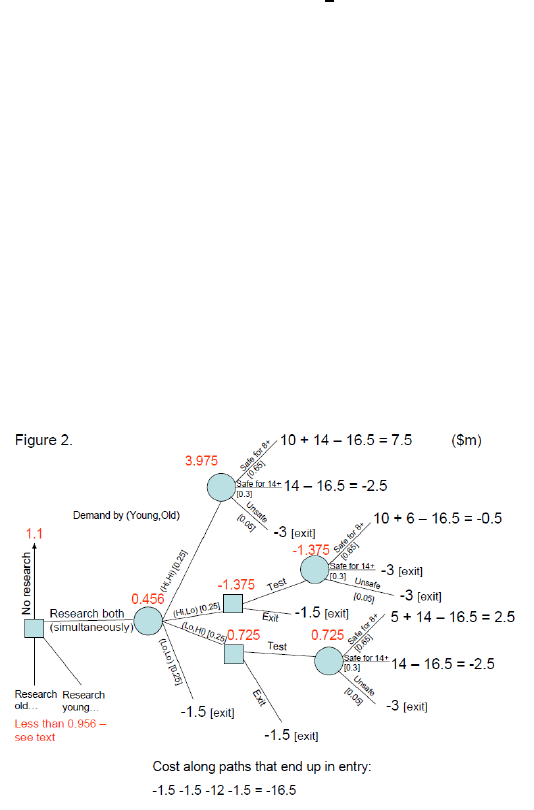
2. Introducing Uncertainty and Time 23
researc h.
(ii) It is never profitable to do researc h after the safety test. If the re-
sult w e re “safe for both groups” then the only case where info is useful
(i.e. ch a nges the decision to ente r into exit) is if both groups have low
demand. (See Figure 1: exiting payoff −15 is better than the −4 of Low-
Low demand scenario, but less than the payoff under the other three de-
man d scenarios). This demand scenario could be ruled out b y researc h -
ing either group. The expected payoff would be
1
4
(9+1+4−15)−1 25,
i.e., not worth it after pa y ing for the cost of research. Research after find-
ing out that WakAtak is only “safe for old” is obviously not profitable,
since even if the information caused the decision to c ha ng e (from “exit”
to “enter,” if demand is high) this results only in a pa yoff of −1 before
the researc h cost, w hile exit guarantees −15; since r esea rch is mo re
costly than the 0:5 difference it canno t be w or thwhile.
(iii) The potential benefit of researc h is that it allow s WakTek to sa ve
the cost of production line under unfavorable demand conditions, so
there w ou ld be no point in plans of action where research is conducted
after the production line is built.
Consider a plan where both groups are researched sim u ltaneously.
This would lead to e xpected value of $0.456 million, so not doing re-

24 2. Introducing Uncertainty and Time
search is better than researching both simultan eously. We can now de-
duce that researching only one of the group s cannot be optimal either.
The reason is th at it is less inform ative than researching both, so th e
expected payoff could not be higher than $0.456 million for any other
reason than the fact that it is cheaper by $(15 −1=05) million. This
means that the expected value (EV ) of a plan where only one group is
researc h ed must be lower than ($0456 + $05=$0956) million. Thus
the $1.1 million value from no research is still the highest. Similar ly,
consider the possibilit y of researc hing both groups sequentially. This is,
at best, equally infor m ative as researchin g both groups simultan eously.
It offers the added option of stopping the research after finding out
the results for one group, and thu s potentially a saving of $0.5 million
comp ared to the cost of researc hin g both sim u lta neou sly. Again, this
cost-saving could not increase the EV to abo ve $0.956, so the optimal
plan of action for part a) is not affected.
(d) Suppose that demand is not independen t across demographics after all,
but instead is perfectly correlated (i.e., if deman d is high in one dem o-
graphic , then it is for sure high in the oth er one as w ell). How, if at all,
w ould that change y our answer to part c)?
Answ er: Now researc h ing either one of the demog raphic groups is
just as in formative as resea rching both (bu t c h ea per, at $1 million);
it tells WakTek whether the dem a nd is high for both groups or low for
both groups. In this case the optimal decision w o uld be to research one
(doesn’t matter which) group, and do the safety testing if the dema nd
is high for both group s, then build the production line and launch the
product unless deemed unsafe; This results in EV of $1.7375 million.
The follow ing figure show s the decision tree.
3
3
Note that exp ected values are not directly axoected by the correlation so the E V of no research is still 1.1.
However, the correlation of dem ands is goo d for WakTek, not just b ecause it m akes m arket research cheap er.
For example, compared to the case (in part c) w here WakTek researches b oth groups simultaneously, one ad ded
benefit here is that WakTek will n ever have to “waste” the cost of safety-testing in the event where the result
turns out to be “safe for old only,” which leads to exit.
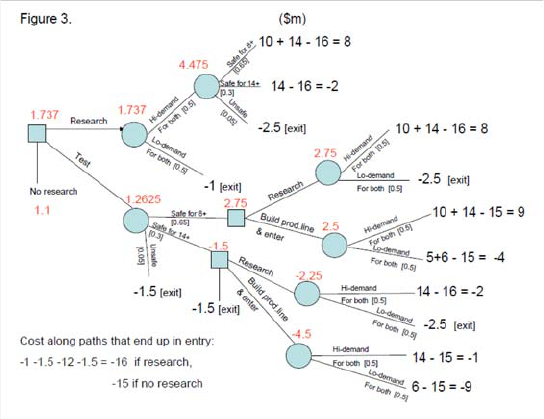
2. Introducing Uncertainty and Time 25
8. Juice: Bozoni is a reno w n ed Swiss ma ker of fruit and vegeta ble juice, w hose
products are sold at specialty stores around Western Europe. Bozoni is con-
sidering whether to add c her imoya juice to its line of products. “It w ou ld
be one of our more difficult varieties to produce and distribute,” observ es
Johann Ziffenboeffel, Bozoni’s CEO. “The cherim oya would be flowninfrom
New Zealand in firm , unripe form , and it w ou ld need its o w n dedicated ripen-
ing facility her e in Europe.” Three succ essful steps are absolute ly necessary
for the new c herimo ya variety to be worth producing. The industrial ripen-
ing process must be shown to allow the delicate flavors of the cherimoya
to be preserved; the testin g of the ripening process requires th e building
of a small-sc ale ripening facilit y. M arket research in selected small regions
around Europe must sho w that there is sufficien t demand am ong consumers
for cherimo ya juice. And cherimo y a juice m ust be sho wn to withstand the
existing tin y gaps in the cold chain bet ween the Bozoni plan t and the end
consumers (these gaps would be prohibitively expensive to fix). Once these
three steps have been completed , there are about 2,500,000 worth of ex-
penses in lau nching the new variety of juice. A successful new variet y w ill
then yield profits, in expected presen t-value terms, of 42.5 m illion.

26 2. Introducing Uncertainty and Time
The three absolutely necessary steps can be done in parallel or sequentially
in any order. Data about these three steps is given in Table 1. “Prob ability
of success” refers to how lik ely it is that the step will be successful. If it is not
successful, then that means that cherim oya juice cannot be sold at a profit.
All pro babilities are ind ependent of each other (i.e., whether a giv en step is
successful or not does not affect the probabilities that the other steps will be
successful). “Cost” refers to the cost of doing this step (regardless of whether
it is successful or not).
(a) Suppose Mr. Ziffen boeffel calls y ou and asks y ou r advice about the
project. In particular, he wants to know (i) should he do the three
necessary steps in parallel (i.e., all a t once) or should he do them se-
quentially; and (ii) if sequentially, w hat’s the righ t order for the steps
to be done? What answers do y ou give him?
Answ er: Bo zoni should do the steps sequentially in this order: first test
the cold cha in, then the ripening process, then do the test-marketing.
The expected value of profits is 1.84 million. Observe that it wo uld not
be profitable to launc h the product if Bozoni had to do all the steps
simultane ou sly. This is an exam ple of real options– by sequencin g the
steps, Bozoni creates options to switc h out of a doomed project before
too much money gets spen t. ¥
(b) Mr. Ziffenboeffel calls you back. Since Table 1 wa s produced (see below ),
Bozoni has found a small research firm that can perform the necessary
tests for the r ipening process at a lower cost than Bozoni’s in-house
researc h department.
Table 1: D ata on launching the Ch erimoya juice
Step Pr o b a bility of succes s Cost
Ripening process 0.7 1,000,000
Test marketing 0.3 5,000,000
Cold chain 0.6 500,000
At the same time, th e EU has raised the criteria for getting approval
for new food producing facilities, which raises the costs of these tests.
2. Introducing Uncertainty and Time 27
Mr. Ziffenboeffel would, therefore, like to kno w how your answe r to (a)
c h ang es as a function of the cost of the ripening test. What do you tell
him?
Answ er: This is sensitivit y analysis for the cost of testing the ripening
process. This can be done by varying the cost for ripening, and seeing
which expected payoff (highlig hted y ellow) is highest for which values of
the cost. For example, whenever w e set the cost below 375,000 it turns
out that the pa yoff from the sequence → → giv es the highest
pa y off among the six possible sequences. (Excel’s GoalSeek is a partic-
ularly handy wa y for finding the threshold v alues quic k ly).
Specifically, the optimal sequence is
i) → → if the cost of ≤ 375 000
ii) → → if the cost of 375 000 ≤ ≤ 2 142 857
iii) → → if the cost of 2 142 857 ≤ ≤ 8 640 000
iv) don’t launch if costsmorethan8 640 000
where “” stands for th e ripening process, “” stands for the cold
c hain, and “ ” stands for test marketing. ¥
(c) Mr. Ziffenboeff
el calls you back y et again. The good news is the EU
regulations and the ou tsourcing of the ripening tests “ balan ce” eac h
other out, so the cost of the test rem ains 1,000,000. No w the problem
is that his marketing department is suggesting that the probabilit y that
the market researc h will result in good news about the deman d could
be differen t in light of some recen t data on the sales of other subtropical
fruit products. He would, therefore, like to kno w how your answer to
(a) c ha nges as a functio n of the probability of a positiv e result from the
market researc h. What do you tell him?
Answ er: This can be found b y varying th e probability of success for
test mark eting (highlighted by blue in the excel sheet) bet ween 0 and
1. The optimal sequence turns out to be

28 2. Introducing Uncertainty and Time
i) don’t launch if ≤ 01905
ii) → → if 01905
where is the probability that the test marketing will be successful.
¥
9. Steel: AK Steel Hold ing Corporation is a producer of flat-rolled carbon,
stainless and electrical steels and tubular products through its wholly o w ned
subsidiary, AK Steel Corporation. The recent surge in the demand for steel
significan tly increased AK ’s profits,
4
and it is no w engaged in a research
project to improve its production of rolled steel. The research involves three
distinct steps, eac h of whic h must be successfully completed before the firm
can implement the cost-sa ving new production process. If the research is
completed successfully, it will save the firm $4 million. Unfortunately, there
is a c ha nce that one or more of the research steps might fail, in which case
the project is worth less. The three steps are done sequen tially, so that the
firm knows whether one step w as successful before it has to in vest in the next
step.Eachstephasa08 probabilit y of success and eac h step costs $500 000.
The risks of failure in the three steps are uncor relate d with one another. AK
Steel is a risk neutral company. (In case you are worried about such things,
the interest rate is zero).
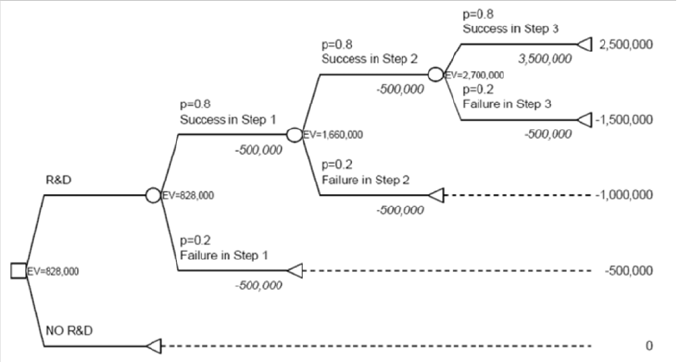
(a) Dra w the decision tree for the firm.
Answ er:
4
See “Demand Send s A K Steel ProfitUp32%,”New York Time, 07/23/2008.
http://www.nytimes.com/2008/07/23/business/23steel.html?partner=rssnyt&emc=rss
2. Introducing Uncertainty and Time 29
¥
(b) If the firm proceeds with this project, what is the probabilit y that it
will succeed in implementing the new production process?
Answ er: For the project to be successful, each of the three independen t
steps must be complet ed. Since the probability of success in eac h stage
is 0.8 and the probabilities are independen t, the probabilit y of three
successes is =08 · 08 · 08=08
3
=0512, just over one-half. ¥
(c) If the researc h were costless, what would be the firm ’s expected gain
from it before the project began?
Answ er: E[]=0512 · $4 000 000 + 0488 · 0=$2 048 000¥
(d) Should the firm begin the researc h , given that each step costs $500 000?
Answ er: The expected cost of the project is
02·$500 000+08·02·$1 000 000+08·08·$1 500 000 = $1 220 000
The first term is the probability times cost of a failure in the fir st step.
The second term is the probabilit y times cost of success in the first step
and failure in the second step. The third term is the probability times
cost of success in the first step and success in the second step (success
or failure in the third step does not affect the cost of the project, just
30 2. Introducing Uncertainty and Time
the gain from it). The expected cost is less than the expected gain (b y
$828,000). Since the company is not risk averse, it shou ld begin the
project. Note that this is not the only way to do the calculation. An
alternate approach w o uld be to aggregate the costs and benefits of each
possible outcom e:
08 · 08 · 08 · (4 000 000 − 500 000 − 500 000 − 500 000)
+08 · 08 · 02(−500 000 − 500 000 − 500 000)
+08 · 02(−500 000 − 500 000) + 02(−500 000)
=$828 000
Either way, the expected net gain is $828 000. ¥
(e) Once the researc h has begun, should the firm quit at any poin t ev en if
it has had no failures? should it ever continue the researc h ev en if it has
had a failure?
Answ er: NO to both. Obviously, if one stage fails, then the project
cannot be com pleted successfully, so any mo re expenditures on it are a
waste. If no stage has failed a nd at lea st one h as succeeded, then th e
benefit/cost comp arison of going forward with the project is even more
favorable than when the project began. ¥
After the
firm has successfully completed steps one and t wo, it discov-
ers an alternate production process that w ould cost $150 000 and would
lo wer production costs b y $1 000 000 with certainty. This process, how-
ever, is a substitute for the three-step cost-saving process; they cannot
be used sim ulta neously. Furthermor e, to have this process available, the
firm m ust spend the $150 000 before it know s if it will successfully
comp lete step three of the three-step research project.
(f) Draw the augmented decision tree that includes the possibility of pur-
suing this alternate production process.
Answ er:
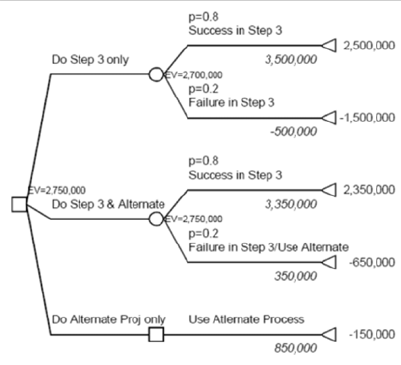
2. Introducing Uncertainty and Time 31
(g) If the firm continues the three-step project, what is the cha nce it would
get any value from also developing the alternate production process?
Answ er: Th e alt erna te process would be used only if step three of the
current project failed, which has a 0.2 probab ility. ¥
(h) If dev eloping the alternate production process wer e costless and if the
firm con tinues the three-step project, w hat is the expected value that
it would get from ha ving the alternate production process available (at
the beginning of researc h step 3)? (This is known as the option value of
ha ving this process a vailable.)
Answ er: There is a 0.2 probabilit y that the alternate process would be
used and a $1,000,000 value if it is used, so the option value of having
thealternateprocessavailableis$200,000.¥
(i) Should the firm:
i. Pursue only the third step of the three-step project
ii. Pursue only alternate production process
iii. Pursue both the third step of the three-step project and the alter-
nate process
32 2. Introducing Uncertainty and Time
Answ er: Since the option value of the alternate process is greater
than the cost of having this option, the alternate process should
be developed if one con tinues with the three-step project. The net
value of developing this option is $200 000 − $150 000 = $50 000.
Of course, the alternate process wo uld also be developed if the
three-step project w ere unavailable, since it will be used with cer-
taint y and the net value of the altern ate process would then be
$850,00 0. The remainin g question is whether AK should drop the
three-step project rather than attempting the third step. Giv en
that the alternate process will be developed, the extra (or mar-
ginal ) value of successfully completing the three-step project wo u ld
be $3,000,000, because it w ou ld save $3,000,000 more than the al-
ternate process. The expected value of attemp ting the third step
is then 08 · $3 000 000 = $2 400 000. This is greater than the
$500,000 cost of the third step, so AK should p roceed with th e
three-step project as well as the alternate process, i.e., tak e strat-
egy (iii). ¥
(j) If the firm had kno wn of the alternate production process before it began
the three-step research project, what should it have done?
Answ er: We know that AK should p ursue the alternate process: It
was wo rth doing after successful completion of steps one and two (see
(i)) and wo uld ha ve g rea ter expected value if th e p roba bility of the
three-step project failing were high er . In fact, the option value of the
alternative process declines with each step of success in the three-step
project. At the beginning of step three A K would pay up to $200,000
for the alternate process. Con vin ce yo urself that it w o uld be willing to
pay up to $360,000 for the alternate process at the beginning of step
t wo and up to $488,000 for the alternate process at the beginning of
step one, assuming in each case that it cou ldn’t wait to develop the
alternate later. In fact, the option to wait un til the beginning of the
third period to develop the alternate process could itself be valuab le,
but it isn’t in this case, w h en the process costs $150,000. The other
2. Introducing Uncertainty and Time 33
question is whether AK should pursue the three-step project given that
it will ha ve the alternate process available with certain ty. As in (i), the
marg inal value of successfully completing the three-step project wou ld
be $3,000,000, because it w ould sav e $3,000,000 more than the alternate
process. The expected value of attempting the three-step project is then
0512 · $3 000 000 = $1 536 000. Th is is greater than the the expected
cost of pursuing the three-step project, which is 02 · 500 000 + 08 · 02 ·
1 000 000 + 08 · 08 · 1 500 000 = 1 220 000, so AK should proceed
with the three-step project as w ell as the alternate process. This is the
same calculation as in (c) and (d) except the benefit of success is no w
$3,000,000 instead of $4,000,000. ¥
10. Surgery: A patient is very sick, and will die in 6 months if he goes un trea ted.
The only available treatment is risky surgery. The patien t is expected to live
for 12 months if the surgery is successful, but the probability that the surgery
fails and the patient dies immed ia tely is 0.3.
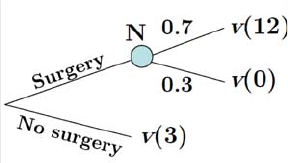
(a) Dra w a decision tree for this decision problem .
Answ er: Using () to denote the value of living more months, the
follow ing is the decision tree:
¥
(b) Let () be the patien t’s pa yoff function, where is the n umber of
mon ths till death. Assuming that (12) = 1 and (0) = 0,whatisthe
lowest payoff thepatientcanhaveforliving3monthssothathaving
surgery is a best response?
Answ er: The expected value of the surgery giv en the pa yoffsaboveis
[(surgery)] = 07(12) + 03(0) = 07

34 2. Introducing Uncertainty and Time
which implies that if (3) 07 then the surgery should be performed. ¥
For the rest of the problem , assume that (3) = 08.
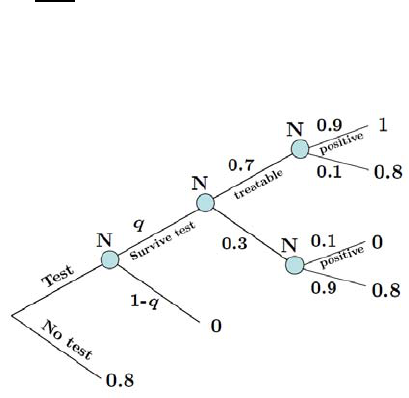
(c) A test is a vailable that will provid e some informatio n that predicts
wheth er or not surgery will be successful. A positive test implies an
increased likelihood that the patient will survive the surgery as follows:
True- p ositive rate: Th e probab ility that the results of this test will
be positive if surgery is to be successful is 0.90.
False-positive rate: The probability that the results of this test will
be positive if the patient will not survive the operation is 0.10.
W ha t is the prob ab ility of a successful surgery if the test is positive ?
Answ er: The easiest way to think about this is to imagine that the
original 0.7 probability of success is true because for 70% of the sic k
populatio n, call these the “treatable” patients, the surgery is success-
ful, while for the other 30% (“untreatab le”) it is not, and previously
the patient did not know which population he belongs to. The test can
be though t of as detecting which population the patien t belongs to.
The abo ve description means th at if the patient is treatable then the
test will claim he is treata b le with proba bility 0.9, while if the patie nt
is un trea ta ble then the test will claim he is treatable with probability
0.1. Hence, 63% of the population are treatable and detected as such
(0.7×09), while 3% of the population are untre atable but are detected
as treatable (0.3×01). Hence, of the population of people for whom the
test is positive, the probability of successful surgery is
63
63+3
=0955 ¥
(d) Assuming that the patient has the test done, at no cost, and the result
is positiv e, should surgery be performed?
Answ er: The value from not having surgery is (3) = 08, and a positive
test updates the probability of success to 0955 with the expected payoff
being 0955 × 1 so the patient should ha ve surgery done. ¥
2. Introducing Uncertainty and Time 35
(e) It turns out that the test may ha v e some fatal complications, i.e., the
patient ma y die durin g the test. D raw a d ecision tree for this revised
problem.
Answ er: Given the data above, we kno w that without taking the test
thepatientwillnothavesurgerybecausetheexpectedvalueofsurgery
is 0.7 while the value of living 3 months is 0.8. Also, we showed abo ve
that after a positive test the patient will choose to have surgery, and it
is easy to sho w that after a negative test he won’t (the probability of
a successful outcome is
7
7+27
=0206) Hence, the decision tree can be
collapsed as follow s 9the decision to have surg ery ha ve been collapsed
to the relevant payoffs):
¥
(f) If the proba bility of death during the test is 0.005, should the patient
opt to have the test prior to deciding on the operation?
Answ er: From the decision tree in part (e), the expected value con di-
tional on surviving the test is equal to
07(09 × 1+01 × 08) + 03(01 × 0+09 × 08) = 0902
which implies that if the test succeeds with probabilit y 0.995 then the
expected pa yoff from taking the test is
0995 × 0902 + 0005 × 0=0897
36 2. Introducing Uncertainty and Time
which implies that the test should be tak en because 0897 08. ¥
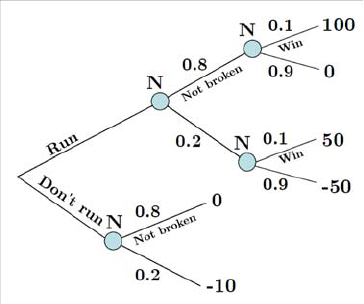
11. To Run or not to Run: You’re a sprinter, and in practice toda y y ou fell
and h u rt y o ur leg. A n x-ray suggests that it’s broken with probabilit y 0.2.
Your problem is whether you should participate in next week’s tournamen t.
If you run, you think you ’ll win w ith probability 0.1. If you r leg is b roken
and y ou run, then it will be further damaged and y our payoffs are as follo w s:
+100 if you win the race and y ou r leg isn’t br oken;
+50 if y o u win and y ou r leg is broken;
0 if you lose and your leg isn’t broken;
−50 if you lose and your leg is broken;
−10 if you don’t run and if y our leg is brok en;
0 if you don’t run and your leg isn’t brok en.
(a) Dra w the decision tree for this problem.
Answ er:
¥
(b) What is your best c h oice of action and its expected pa yoff?
Answ er: The expected pay off from not running is
[(not run)] = 08 × 0+02(−10) = −2
and the expected pa yoff from running is
[(run)] = 08×(01×100+09×0)+02×(01×50+09×(−50)) = 0
2. Introducing Uncertainty and Time 37
so the best c h oice is to run and have an expected payoff of 0. ¥
You can gather some more inform a tion by having more tests, and y ou
can gather more information about whether y ou ’ll win the race b y talk-
ingtoyourcoach.
(c) What is the value of perfect inform ation about the state of yo ur leg?
Answ er: If you knew you r leg is broken then running yields an expected
pa y off of 01×50+09×(−50) = −40 while not running yields a pay off
of −10,soyouwouldnotrunandget−10.Ifyouknewyourlegisnot
broken then the expected payoff from runnin g is 01×100+09×0=10,
while the pay off from not running is 0, and hence you would run and
get 10. Before getting the information you know your leg is broken
with proba b ility 0.2, so before getting the perfect inform ation , your
expected pa yoff from being able to then act on the perfect inform a tion
is 02(−10) + 08 × 10 = 6. Recall from (b) that the expected payoff of
not ha vin g perfect information is 0, so the value of being able to obtain
the perfect inform ation is 6 − 0=6. ¥
(d) What is the value of perfect information about whether you’ll win the
tournam ent?
Answ er: In this case we know that you will run if y ou know y o u will
win and y ou will not if you know you will lose. Hence, with probability
01 yo u will learn that you’ll win and your expected payoff (depending
on the state of yo ur leg) is 02 × 100 + 08
× 50 = 60Similarly, with
probab ility 0.9 you learn that you’ll lose in wh ich case you r expected
pa y off is 02 × (−10)+ 08 × 0=−2. Before getting the information y ou
know you will win with probab ility 0.1, so before getting the perfect
information, y our expected pa yoff frombeingabletothenactonthe
perfect information is 01 × 60+ 09(−2) = 42.Recallfrom(b)thatthe
expected payoff of not ha v in g perfec t informa tio n is 0,sothevalueof
beingabletoobtaintheperfectinformationis42 − 0=42. ¥

38 2. Introducing Uncertainty and Time
(e) As stated above, the probabilit y that your leg is broken and the proba-
bilit y that y ou will win the tournamen t are independent. Can y ou use a
decision tree in the case that the probability that you will win the race
depends on whether y our leg is broken?
Answ er: Yes. All you need to do is have different proba bilities of win-
ning that depend on whether or not y our leg is brok en. ¥
12. Mo re O il: Ch evron, the No. 2 US oil company, is facing a tough decision.
The new oil project dubbed “Tahiti” is sch eduled to produce its first comm er-
cial oil in mid-2008, ye t it is still unclear how productiv e it will be. “Tahiti
is one of Chevron’s fiv e big projects,” told Peter Robertson, vice ch airm an
of the compan y’s board to the Wall Str eet Journal.
5
Still, it was unclear
wheth er the project will result in the blockb u ster success Chevron is hop ing
for. As of June 2007, $4-billion has been in vested in the high-tec h deep sea
platform, w hic h suffices to perform early w ell tests. Aside from offering in-
formation on the type of reservoir, the tests will produce enough oil to just
co ver the incremental costs of the testing (beyond the $4 billion investm ent).
Follo win g the test we lls, Chevron predicts one of three possible scenarios.
The optim istic one is that Tahiti sits on one giant, easily accessible oil reser-
voir, in whic h case the compa ny expects to extract 200,000 barrels a da y
after expending another $5 billion in platform setup costs, with a cost of
extraction at about $10 a barrel. This will continue for 10 years, after whic h
the field will have no more econom ically recoverable oil. Chevron believes
this scenario has a 1 in 6 c h an ce of occurring. A less rosy scen ario, that is
twice as lik ely as th e optim istic one, is that Chev ro n wo uld ha ve to drill
t wo more w e lls at an additional cost of $0.5 billion each (above and beyo nd
the $5 billion set-up costs), and in w hich case production will be around
100,000 barrels a day with a cost of extraction at about $30 a barrel, and
the field will still be depleted after 10 years. The worst case scenario in volves
5
“C h e v ron’s Tahiti Facility Bets Bi g on G u lf O il Boo m.” Jun 2 7, 20 0 7 . pg. B 5 C.
http://proquest.umi.com/pqdweb?did=1295308671& sid=1&Fmt=3&clientId=1566&RQT=309&V Name= PQD

2. Introducing Uncertainty and Time 39
the oil tucked awa y in n um ero us poc kets, requiring expensive water injection
tec h n ique s which w o uld include up-front costs of another $4 billion (abo ve
and bey on d the $5 billion set-up costs), extraction costs of $50 a barre l, and
production is estimated to be at about 60,000 barr els a day, for 10 y ea rs.
Bill Varnado, Tahiti’s project manag er, was quoted giving this least desir-
able outcome odds of 50-50.
The curren t price of oil is $70 a barrel. For simplicity, assum e that the price
of oil and all costs will remain constant (adjusted for inflation) and that
Chevr on’s faces a 0% cost of capital (also adjusted for inflation).
(a) If the test-wells w o uld not produce information about whic h one of three
possible scenarios will result, should Ch evron invest the set-up costs of
$5 billion to be prepared to produce at wh atever scenario is realized?
Answ er: We start b y noticing that the $2 billion that were in vested are
a sunk cost and hence irrelevant. Also, since the cost of capital is just
about the same as the projected increase in oil prices, w e do not need to
discount future oil reven ues to get the net present value (NPV) sine the
two effects (price increase and tim e discounting) will cancel each other
out. If the com p any in vests the $2 .5 billion dollar s, then they will be
prepared to a ct upon whatev e r scenario arises (great with probabilit y
1
6
, ok with pro bability
1
3
or bad w ith probabilit y
1
2
). N otice from the
table belo w that in eac h scenario the added costs of extraction that
Chevron need s to invest (once it becomes clear whic h scenario it is) is
worthwhile (e.g., even in the bad scenario, the profits are $2.19 billion,
which covers the added drilling costs of $2 billion in this case.) Hence,
Chevron wou ld proceed to drill in eac h of the three scenarios, and the
expected profits inclu din g the init ia l $2.5 billion investm e nt would be,
=
1
6
×($21)+
1
3
×($73−$05)+
1
2
×($219−$2)−$25 =$3 511 666 667
(b) If the test-w ells do produce accura te info rm ation about which of three
possible scenarios is true, what is the added value of performing these
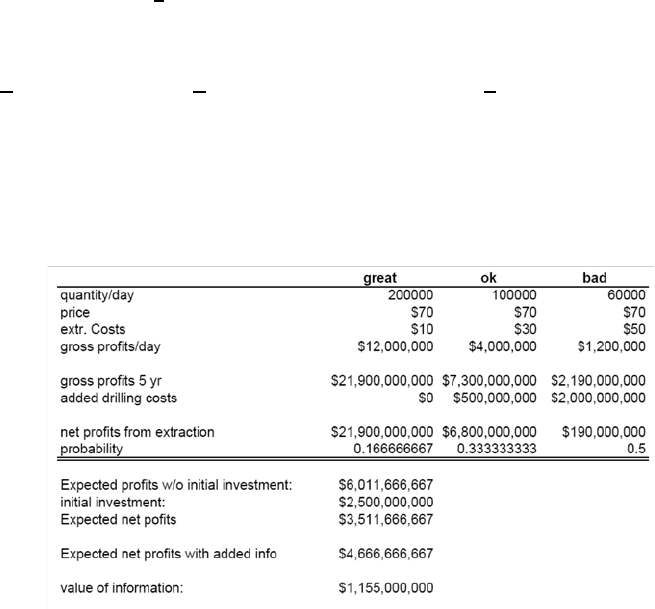
40 2. Introducing Uncertainty and Time
tests?
Answ er: Now, if the test drilling will revea l the scenario ahead of time,
then in the event of the bad scena rio the revenues w ou ld not cover the
total in vestment of $4.5 billion ($2.5 billion initially, a nd another $2
billion for the bad scenario.) In the great and ok scenarios, ho wever,
the revenues cover all the costs. Hence, with the inform atio n Chevron
would not p roceed with the investm ents at all when the bad scenario
happens (probability
1
2
), and proceed only when the scenario is great or
ok, yielding an expected profitof
=
1
6
×($21−25)+
1
3
×($73−$25−$05)+
1
2
×0=$4 666 666 667
Hence, the added value of perfor m ing the tests is,
info
=$4 666 666 667 − $3 511 666 667 = $1 155 000 000
¥
13. To day, Tomorrow or the Day after: Aplayerhas$100 toda y that need
to be consum ed o ver the next three periods, =1 2 3. The utility over
consuming $
in period is given by the utility funct ion ()=ln(),and
at period =1, the player valu es his net presen t value from all consum p tion
as (
1
)+(
2
)+
2
(
3
),where =09

2. Introducing Uncertainty and Time 41
(a) How w ill the player plan to spend the $100 over the three periods of
consumption?
Answ er: The player will max imize
max
1
2
ln(
1
)+ ln(
2
)+
2
ln(100 −
1
−
2
)
which yield s the followin g two first-order equations:
1
1
−
2
100 −
1
−
2
=0
2
−
2
100 −
1
−
2
=0
From these two equation s conclude that
1
1
=
2
or
2
=
1
. We can then then substitute
2
with
1
in the first equa-
tion above to obtain,
1
1
−
2
100 −
1
−
1
=0
or
100 −
1
−
1
−
2
1
=0
and the solution is
1
=
100
+
2
+1
and in turn
2
=
100
+
2
+1
,and
3
=
2
100
+
2
+1
. ¥
(b) Imagine that the pla yer know s that in period =2he will receiv e an
additional gift of $20 How will he ch oose to allocate his original $100
initially, and how will he spend the extra $20?

42 2. Introducing Uncertainty and Time
Answ er: After spending
1
≤ 100, the player has 100 −
1
+20in the
beginnin g of the second period. We can now solv e this backward and
assume that the pla yer has 100 −
1
+20in the beginning of period 2
and has to choose between
2
and
3
so that he solv e,
max
2
ln(
2
)+ ln(120 −
1
−
2
)
with the first order condition
1
2
−
120 −
1
−
2
=0
which yields,
2
=
120 −
1
1+
and
3
=
(120 −
1
)
1+
Now we can step back to the first period and solve the optimal c h o ice
of
1
given the w a y
2
and
3
will be chosen later. The pla y er solves,
max
1
2
ln(
1
)+ ln(
120 −
1
1+
)+
2
ln(
(120 −
1
)
1+
)
and the first order condition is,
1
1
−
(1 + )
120 −
1
×
1
1+
−
2
(1 + )
120 −
1
×
1
1+
=0
or
1
=
120
1+ +
2
.
Notice, howev er, that as drops,
1
increases, and for a small enough
this equation will call for
1
100. In particular, the value of for
which
1
=100canbesolvedasfollows,
100 =
120
1+ +
2
or, =
3
10
√
5 −
1
2
≈ 017. Ho wever,
1
100 is not possible, so the
solution is,
1
=
120
1++
2
if ≥ 017
100 if 017

2. Introducing Uncertainty and Time 43
and from the calculations earlier,
2
=
120 −
1
1+
and
3
=
(120 −
1
)
1+
¥
Part II
Static Gam es of Com plete
Information
44
This is page 45
Printer: Opaque
t
3
P r elimina r ies
1. eBa y: Hund red s of millions of people bid on eBa y auctions to purchase goods
from all over th e world. Despite being done online, in spirit these a uction s
are similar to those conducted cen turies ago. Is an auction a game? W h y or
wh y not?
Answ er: An auction is indeed a game. A bidder’s payoff depends on his bid
and on the bid of other bidders, and hence there are players, actions (whic h
are bids) and pa yoffs that depend on all the bids. Th e winner gets the item
andpaystheprice(whichoneBayisthesecondhighestbidplustheauction
increm ent), while the losers all pay nothing and get nothing. ¥
2. Pena lty Kicks: Imagine a kick er and a goalie who confron t each other in a
penalty kic k that will determine the outcom e of the gam e. The kicker can kick
theballleftorright,whilethegoaliecanchoosetojumpleftorright.Because
of the speed of the kick, the decision s need to be made simultaneously. If the
goalie jumps in the same direction as the kick, then the goalie wins and the
kic ker loses. If the goalie jumps in the opposite direction of the kick then the
kic ker wins and the goalie loses. M odel this as a normal form game and write
down the matrix that represents the game yo u modeled.

46 3. Preliminaries
Answ er: There are two pla yers, 1 (kic ker) and 2 (goalie). Each has two
actions,
∈ { } to denote left or right. The kicker wins when they
c h oose opposite directions while the goalie wins if they ch oose the same
direction. Using 1 to denote a win and −1 to denote a loss, w e can w rite
1
( )=
1
( )=
2
( )=
2
( )=1and
1
( )=
1
( )=
2
( )=
2
( )=−1. The matrix is therefore,
Play er 1
Player 2
−1 1 1 −1
1 −1 −1 1
¥
3. Meeting Up: Tw o old friends plan to meet at a conference in San Francisco,
and agreed to m eet by the to wer. When arriving in tow n , each realizes that
there a re two natural choices: Sutro To wer or C oit Tower. Not having cell
phones, eac h m ust c hoose independently which tower to go to. Eac h pla y er
prefers meeting up to not meeting up, and neither cares w her e this would
happen. Model this as a normal form came, and write dow n the matrix form
of the game.
Answ er: There are t w o play ers, 1 and 2.Eachhastwoactions,
∈ { }
to denote Sutro or Coit. Both players are happ y if they choose the same
to wer and unhapp y if they don’t. Using 1 to denote happ y and 0 to denote
unhapp y, we can write
( )=
( )=1and
( )=
( )=0
for ∈ {1 2}. The matrix is therefor e,
Player 1
Player 2
1 1 −1 −1
−1 −1 1 1
¥

3. Preliminaries 47
4. Hunting: Two hunters, players 1 and 2 can eac h ch oose to h u nt a stag,
which provides a rather large and tasty meal, or h unt a hare, also tast y, but
much less filling . Hun t in g stags is c hallen gin g and requires m ut ua l coopera-
tion. If either hunts a stag alone, then the stag will get away, while h u nting
the stag together guarantees that the stag is caught. Hun ting hares is an
individualistic enterprise that is not done in pairs, and whoever c hooses to
hunt a hare will catch one. The payoff from hunting a hare is 1, while the
pa y off to each from hu nting a stag together is 3. The pa yoff from an unsuc-
cessful stag-h u nt is 0.Representthisgameasamatrix.
Answ er: This is the fam ous “stag hunt” game. Using for stag and for
hare, the matrix is,
Player 1
Player 2
3 3 0 1
1 0 1 1
¥
5. Matc hing P ennies: Players 1 and 2 both put a penny on a table sim ul-
taneously. If the t wo pennies come up the same side (heads or tails) then
play er 1 gets both pennies, otherwise pla yer 2 gets both pennies. Represent
this game as a matrix.
Answer: Letting denote a c hoice of heads and a c ho ice of tails, and
letting winning giv e a pa y off of 1 while losing gives −1, the m atrix is ther e-
fore,
Play er 1
Player 2
1 −1 −1 1
−1 1 1 −1
¥
6. Price Com petition: Imagine a market with dem an d ()=100−.There
are t wo firms, 1 and 2, and each firm has to sim ultaneously choose it’s price

48 3. Preliminaries
.If
,thenfirm gets all of the m ark et while no one demands the
good of firm . If the prices are the same then both firm s equally split the
mark et demand. Imagine that there are no costs to produce any quantit y
of the good. (These are two large dairy farms, and the product is man ure.)
Write do w n the norm al form of this game.
Answ er: The players are = {1 2} and the strategy sets are
=[0 ∞]
for ∈ {1 2} and firms choose prices
∈
.Tocalculatepayoffs, we need
to kno w what the qua ntities will be for eac h firm giv en prices (
1
2
).Given
the assump tion on ties, the quantities are given by,
(
)=
⎧
⎪
⎨
⎪
⎩
100 −
if
0 if
100−
2
if
=
whichinturnmeansthatthepayoff function is given by quantit y times price
(there are no costs):
(
)=
⎧
⎪
⎨
⎪
⎩
(100 −
)
if
0 if
100−
2
if
=
¥
7. Pu blic Good Co ntribution: Three pla y ers live in a town and eac h can
c h oose to contribu te to fund a street lamp. T h e value of having the street
lam p is 3 for eac h player and the value of not having one is 0.TheMayor
asks eac h pla yer to either contrib ute 1 or nothing. If at least two pla yers
con trib ute then the lam p will be erected. If one or less people con tribu te
then the lamp will not be erected, in which case an y person wh o contribu ted
will not get their money back. Write dow n the normal form of this game.
Answ er: The set of players is = {1 2 3} and eac h h as an strategy set
= {0 1} where 0 is not to con tribute and 1 is to contribu te. The payoffs
3. Preliminaries 49
of player fro m a profile of strategies (
1
2
3
) is given by,
(
1
2
3
)=
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
0 if
=0and
=0for some 6=
3 if
=0and
=1for both 6=
−1 if
=1and
=0for both 6=
2 if
=1and
=1for some 6=
¥
50 3. Preliminaries

This is page 51
Printer: Opaque
t
4
Rat io n ality a n d C o mm o n Knowled g e
1. Prove Proposition ??:IfthegameΓ = h{
}
=1
{
}
=1
i has a strictly
dominan t strategy equilibrium
,then
is the unique dominant strateg y
equilibrium .
Answ er: Assume not. That is, there is some other strategy profile
∗
6=
that is also a strictly dominant strategy equilibrium . But this implies that
for ev ery ,
∗
, which contradicts that
is a strictly dominant strategy
equilibrium . ¥
2. Weak dominance. We call the strategy profile
∈ is a weakly domi-
nant strategy equilibriu m if
∈
is a wea kly dominant strategy for all
∈ .Thatisif
(
−
) ≥
(
0
−
) for all
0
∈
and for all
−
∈
−
.
(a) Provide an example of a game in whic h there is no weakly dominan t
strategy equilibrium.
Answ er:
Player 1
Play er 2
1 −1 −1 1
−1 1 1 −1

52 4. Rationality and Common Knowledge
¥
(b) Pro vide an exam ple of a game in whic h there is more than one we akly
dom inant strategy equilibrium .
Answ er: In the follow ing gam e each pla yer is indifferent between his
strategies and so each one is weakly dominated by the other. This means
that an y outc om e is a weakly dom ina nt strategy equilibrium.
Player 1
Play er 2
1 1 1 1
1 1 1 1
¥
3. Discrete first-price auction: An item is up for auction. Player 1 values
the item at 3 while player 2 values the item at 5 Eac h player can bid either
0 1 or 2.Ifplayer bids more than player then win’s the good and pays
his bid, while the loser does not pay. If both pla y ers bid the same amoun t
then a coin is tossed to determine who the winner is, who gets the good and
pa ys his bid while the loser pays nothing.
(a) Write dow n the game in matrix form.
Answ er: We need to determine what the pa y offs are if the bidders
tie. The one who wins the coin toss bids his bid and the loser gets
and pays nothing. Hence, w e can just calculate the expected payoff as a
50:50 lottery betw een getting nothing and winning. For example, if both
pla yers bid 2 then pla yer 1 gets 3 −2=1unit of pa y off with probability
1
2
and pla yer 2 gets 5 − 2=3units of payoff with prob a bility
1
2
,sothe
4. Rationality and Common Kno wledge 53
pair of pa y offsis(
1
2
3
2
)
Player 1
Player 2
012
0
3
2
5
2
0 4 0 3
1 2 0 1 2 0 3
2 1 0 1 0
1
2
3
2
(b) Does an y pla yer have a strictly dominated strategy?
Answ er: Yes-forplayer2bidding0 is strictly dominated b y bidding
2. ¥
(c) Which strategies survive IESDS?
Answ er: After removing the strategy 0 of pla yer 2, pla yer 1’s strategy
of 0 is dominated by 2, so we can rem ove that too. But then, in the
remain ing 2 × 2 game where both pla yers can choose 1 or 2, bidding
1 is strictly dominated by bidding 2 for play e r 2, and after this roun d,
bidding 1 is strictly domina ted by bid ding 2 forplayer1.Hence,the
unique strategy that survives IESD S is (2 2) yielding expected payoffs
of (
1
2
3
2
). ¥
4. eBa y’s recommendation: It is hard to imagine that an yon e is not familia r
with eBay
c
°
, the m ost popular auction website by far. The wa y a typical
eBa y auction w orks is that a good is placed for sale, and each bidder places
a“proxybid”,whicheBaykeepsinmemory.Ifyouenteraproxybidthat
is lo wer than the current highest bid, then y our bid is ignored. If, however,
it is higher, then the curren t bid increases up to one incremen t (say, 1 cent)
abo ve the second highest pro xy bid. For example, im agine that three people
placed bids on a used laptop of $55, $98 and $112. The current price will be
at $98.01, and if the auction ended the player who bid $112 would win at a
price of $9 8.0 1. If you were to plac e a bid of $103.45 then the who bid $11 2
w ould still win, but at a price of $103.46, while if y our bid was $123.12 then

54 4. Rationality and Common Knowledge
y ou w ould win at a price of $112.01.
Now consider eBay’s historical recomme ndation that y ou think hard about
y our value of the good, and that y ou enter your true value as y our bid, no
more, no less. Assume that the value of the good for each poten tial bidder is
independent of ho w m u c h other bidders value it.
(a) Argue that bidding more than y our v aluation is w eakly dominated b y
actually bidding y our valuation.
Answ er: If y o u put in a bid
=
0
where
is yo ur valu a tion , then
only the three follow ing cases can happen: () All other bid s are belo w
.
In this case bidding
=
will yield the exact same outcome: y o u’ll win
atthesameprice.() Some bid is above
0
. In this case bidding
=
will yield the exact same outco m e: you’ll lose to a higher bid. ()No
bids are abo ve
0
and some bid
∗
is in between
and
0
.Inthiscase
bidding
0
willcauseyoutowininandpay
∗
which means that
y our pa y off is negative, while if you w ou ld ha ve bid
=
then you
w ould lose and get nothing. Hence, in cases () and () bidding
would
do as w ell as bidding
0
, and in case () it wo uld do strictly better,
implying that bidding more than you r valuation is w eakly dominated
b y actually bidding y our valuation. ¥
(b) Argue that bidding less t han y o ur valuation is weakly dominated b y
actually bidding y our valuation.
Answ er: If y o u put in a bid
=
0
where
is yo ur valu a tion , then
only the three follow ing cases can happen: () Some other bid are above
.
In this case biddin g
=
will yield the exact sam e outcome: you’ll
lose to a higher bid. () All othe r bids are below
0
. In this case bidding
=
will yield the exact same outcome: you’ll win at the sam e price.
()Nobidsareabove
and some bid
∗
is in between
0
and
.In
this case bidding
0
will cause yo u to lose and get nothing, while if you
would have bid
=
then you would win and get a positiv e payoff of
−
∗
. Hence, in cases () and () bidding
w ould do as well as bidding
0
, and in case () it would do strictly better, im plying that biddin g

4. Rationality and Common Kno wledge 55
less than yo ur valua tion is w ea kly dominate d by actually bidding your
valuation. ¥
(c) Use y our analysis abov e to make sense of eBay’s recommend atio n. Would
y o u follow it?
Answ er: The r ecom mendation is indeed supported by an analysis of
rational beha vior.
1
5. In the follo w ing normal-form game, whic h strategy profiles survive iterated
elimination of strictly dom inated strategies?
Player 1
Player 2
6 8 2 6 8 2
8 2 4 4 9 5
8 10 4 6 6 7
Answ er: First, is dominated b y forplayer1.Intheremaininggame,
is dominated by for play e r 2. No more strategies are strictly dominated, and
hence ( ) ( ) ( ) and ( ) all survive IESDS. (Note: after the
last stage abo ve, is weakly dominated by forplayer1,afterwhich is
dominated b y for player 1, so that ( ) would be the only strategy profile
that w o uld survive iterated elim ination of wea kly domin ated strategies. ¥
6. Roommates: Two roommates need to each c hoose to clean their apartmen t,
and each can ch oose an amount of time
≥ 0 to clean. If their c h oices are
and
,thenplayer’s payoff is given by (10 −
)
−
2
.(Thispayoff function
impliesthatthemoreoneroommatecleans,thelessvaluableiscleaningfor
the other roomm ate.)
1
Th o s e familiar wit h eB ay know abo u t sniping , which i s bid d in g in the last m inut e. It st ill is a we a k ly do min a te d
strategy to bid your valuation at that time, and waiting for the last minute may b e a “best response” if you b elieve
other p eople may respond to an early bid. M ore on this is discussed in chapter 13.
56 4. Rationality and Common Knowledge
(a) What is the best response correspondence of each play e r ?
Answ er: Play er maximizes (10 −
)
−
2
given a belief about
,and
the first-order optimality condition is 10 −
− 2
=0implying that
the best response is
=
10−
2
¥
(b) Whic h c hoices survive one round of IESDS?
Answ er: Themostplayer would choose is
=5,whichisaBRto
=0. Hence, any
5 is do min ated by
=5.
2
Hence,
∈ [0 5] are
the choices that survive one round of IESDS.
(c) Whic h c h oices surviv e IESDS?
Answ er: The analysis follow s the same ideas that were used for the
Courno t duopoly in section 4.2.2. In the second round of elimination,
because
2
≤ 5 the best response
=
10−
2
implies tha t firm 1 will
choose
1
≥ 25, and a symm etric argument applies to firm 2. Hence,
the second round of elimination implies that the surviving strategy sets
are
∈ [25 5] for ∈ {1 2}. If this process w e re to con verge to an
interval, and not to a single point, then b y the symmetry betw een both
pla yers, th e resulting interval for each firm w ould be [
min
max
] that
simultaneou sly satisfy two equations with two unkno w ns:
min
=
10−
max
2
and
max
=
10−
min
2
. Ho wever, the only solution to these t wo equations is
min
=
max
=
10
3
Hence, the unique pair of c hoices that survive IESDS
forthisgameare
1
=
2
=
10
3
. ¥
7. Campaigning: Tw o candidates, 1 and 2, are running for office. They each
ha v e one of three choices in running their campaign: focus on the positive
aspects of one’s o w n platform, call this a positive cam p a ign (or ), focus on
thepositiveaspectsofone’sownplatformwhileattackingone’sopponent’s
2
This can b e shown directly: The payoff from cho o sing
=5when the opp onent is choosing
is (5
)=
(10 −
)5 − 25 = 25 − 5
. T he payoff fro m cho o sin g
=5+ where 0 when th e opp onent is choosing
is
(5 +
)=(10−
)(5+)− (5+)
2
=25−5−
2
−
, and b ecause 0 it follows tha t (5+
) (5
)
4. Rationality and Common Kno wledge 57
campaign, call this a balanced campaign (or ), and finally, focus only on at-
tac king one’s opponent, call this a negative campaign (or ). All a candidate
cares about is the probabilit y of win n ing , so assume that if a candid ate ex-
pects to win with probab ility ∈ [0 1], then his payoff is . The probabilit y
that a candidate wins depends on his c hoice of campaign and his opponen t’s
choice. The proba bilities of winning are given as follo w s:
• — If both choose the same campaign, each wins with probabilit y 0.5.
— If candidate uses a positive campa ign while 6= uses a balanced
one, then loses for sure.
— If candidate uses a positiv e cam paig n wh ile 6= uses a negative
one, then wins with probability 0.3.
— If candidate uses a negativ e campa ign while 6= uses a balanced
one, then wins with probability 0.6.
(a) Model this story as a normal form game. (It suffices to be specificabout
the pa yoff function of one pla yer, and explainin g how the other player’s
pa y off function is differen t and why.)
Answ er: There are t w o pla y ers ∈ {1 2}, each has three strategies
= { } an d the p ayoffsare
( )=
( )=
( )=
05;
1
( )=
2
( )=1;
2
( )=
1
( )=0;
1
( )=
2
( )=03;
2
( )=
1
( )=07;
1
( )=
2
()=06;
and
2
()=
1
( )=04. ¥
(b) Write the game in matrix form.
Answ er:
Play er 1
Player 2
05 05 0 1 03 07
1 0 05 05 04 06
07 03 06 04 05 05
¥
58 4. Rationality and Common Knowledge
(c) What happens at eac h stage of elimination of strictly dominated strate-
gies? Will this procedure lead to a clear prediction?
Answ er: No tice that for each pla yer strictly dom inates .Inthe
remain ing 2 × 2 gam e without the strategies , strictly dominates
for eac h player. Hence, the unique clear prediction is that both candi-
dateswillengageinnegativecampaigns.¥
8. Consider the -Beauty contest presented in section 4.3.5.
(a) Show that if pla yer believes that ev eryon e else is ch oosing 20 then 19
is not the only best response for an y number of pla yers .
Answ er: If everyone else is c h oosing 20 and if player chooses 19 then
3
4
of the avera ge will be somew here belo w 15, and 19 is closer to that
n u mber, and therefore is a best response. Bu t the same argument holds
for any choice of player that is bet ween 15 and and 20 regardless of
the number of players. (In fact, y ou should be able to con vinc e yourse lf
that this will be true for any choice of between 10 and 20.) ¥
(b) Sho w that the set of best response strategies to everyone else c hoosing
the n umber 20 depends on the n umber of play ers .
Answ er: Imagine that =2. If one player is choosing 20, then an y
number
between 0 and 19 will beat 20. This follow s because the target
number (
3
4
oftheaverage)isequalto
3
4
×
20+
2
=
15
2
+
3
8
, the distance
between 20 and the target nu mber is
25
2
−
3
8
(this will always be positive
because the target n umber is less than 20) while the distance between
and the target n umber is
¯
¯
5
8
−
15
2
¯
¯
. The latter will be smaller than
the former if and only if
¯
¯
5
8
−
15
2
¯
¯
25
2
−
3
8
,or−20
20.Given
the constraints on the c ho ices,
∈ {0 1 19}. Now imag ine that
=5. The target number is equal to
3
4
×
80+
5
=12+
3
20
,thedistance
bet ween 20 and the target number is 8−
3
20
whilethedistancebetween
and the target nu mber is
¯
¯
17
20
− 12
¯
¯
. The latter will be smaller than

4. Rationality and Common Kno wledge 59
the former if and only if
¯
¯
17
20
− 12
¯
¯
8 −
3
20
,or
40
7
20. Hence,
= {6 7 19}. You should be able to convince yourself that as
→∞,ifeveryonebut ch ooses 20 then ’s best response will converge
to
= {10 11 19}. ¥
9. Consider the -Beauty contest presented in section 4.3.5. Show that if the
number of players 2 then the c hoices {0 1} foreachplayerareboth
Ratio na liz ab le, while if =2then only the c hoice of {0} by eac h player is
Rationalizable.
Answ er: We start with =2.Ifplayer2 c hooses 0 then pla yer 1’s best
response is clearly 0. Now imag in e that player 2 is ch oosing 1.Ifplayer1
chooses
1
=1then they tie and he wins with probability 05, while if he
chooses
1
=0then the target n umber is
3
8
and he win s for sure. Hen ce, 0 is
a best reply to 1 and only the choice of 0 b y both players is Ratio na lizable.
Now assume that 2. If all player’s but choose 0, then ’s best response
is 0, and hen ce ch oosing 0 is Rationa lizable. Now assume that everyon e but
chooses 1.Ifplayer1chooses
1
=1then he ties. If he c hooses
1
=0then
thetargetnumberis
3
4
×
+1
≥
1
2
because ≥ 2 (it is equal to
1
2
when =2
and greater when 2). Hence, for ≥ 2 the set of Rationalizable choices is
{0 1}. The analysis in the text sho ws that no other c hoice is Rationalizable
when =
3
4
. ¥
10. P opsicle stands: There are five lifeguard towers lined along a beach , where
the left-most tower is number 1 and the righ t most tower is number 5. Two
vendors, pla yers 1 and 2, each have a popsicle stand that can be located next
to one of fiv e to wers. There are 25 people located next to each tower, and
eac h person will purchase a popsicle from the stand that is closest to him or
her. That is, if pla yer 1 locates his stand at tower 2 and p layer 2 at tower
3, then 50 people (at towers 1 and 2) will purc hase from player 1, while 75
(from towers 3,4 and 5) will pu rchase from vendor 2. Eac h purc ha se yields a
profitof$1.
60 4. Rationality and Common Knowledge
(a) Specify the strategy set of each player. Are there any strictly dominated
strategies?
Answ er: The strategy sets for each pla yer are
= {1 25} where
each cho ice represen ts a tower. To see whether there are an y strictly
dom inated strategies it is useful to construct the matrix representation
of this game. Assume that if a group of people are indifferent between
the two places (equidistant) then they will split between the two v en dors
(e.g., if the v end o rs are at the same tower then their payoffs will be 62.5
each, while if they are located at towers 1 and 3 then they split the
people from tower 2 and their payoffs are 37.5 and 87.5 respectively.)
Otherw ise they get the people closest to them, so payoffsare:
Player 1
Play er 2
12345
1 625 625 25 100 375 875 50 75 625 625
2 100 25 625 625 50 75 625 625 75 50
3 875 375 75 50 625 625 75 50 875 375
4 75 50 625 625 50 75 625 625 100 25
5 625 625 50 75 375 875 25 100 62 5 625
Notice that the choices of 1 and 5 are strictly dominated b y any other
c hoice for both players 1 and 2. ¥
(b) Find the set of strategies that survive Rat ionaliza b ility.
Answ er: Because the strategies 1 and 5 are strictly domin ated then
they cannot be a best response to an y belief (P r oposition 4.3). In the
reduced game in whic h these strategies are remov ed , both strategies 2
and 4 are dominated by 3, and therefore cannot be a best response in
this second stage. Hence, only the choice {3} is rationalizable. ¥
This is page 61
Printer: Opaque
t
5
Pinning Down Beliefs: Nash Equilibrium
1. Prove Proposition ??.
Answ er: (1) Assum e that
∗
is a strict dominant strategy equilibrium . This
implies that for an y pla yer ,
∗
is a best response to any c hoice of his oppo-
nents including
∗
−
, whic h in turn implies that
∗
is a Na sh equilibrium.
(2)Assumethat
∗
istheuniquesurvivorofIESDS.Byconstructionofthe
IESDS procedure, there is no round in which
∗
is strictly domina ted against
the surviving strategies of ’s opponents, an in particular, against
∗
−
,imply-
ing that
∗
is a best response to
∗
−
, which in turn imp lies that
∗
is a Nash
equilibrium .
(3) Assume that
∗
is the unique Rationalizable strategy profile. By construc-
tion of the Rationa lizability procedur e, any strategy of player that surviv es
a round of rationalizability can be a best response to some strategy of ’s op-
ponen ts that surviv es that round. Hence, by definition,
∗
is a best response
to
∗
−
, which in turn implies that
∗
is a Na sh equ ilibr ium . ¥
2. A strategy
∈ is a w eakly dom inant strategy equilibrium if
∈
is a weakly dominan t strategy for all ∈ .Thatisif
(
−
) ≥
(
0
−
) for all
0
∈
and for all
−
∈
−
. Pro vide an example of a gam e
62 5. Pinning Down Beliefs: Nash Equilibrium
for which there is a w eakly dominan t strategy equilibrium, as w ell as another
Nash equilibriu m .
Answ er: Con sid er the follo wing game:
Player 1
Player 2
1 1 1 1
1 1 2 2
In this game, ( ) is a we ak ly domin ant strategy equilibrium (and of
cour se, a Na sh equilib riu m), yet ( ) is a Nash equilibrium that is not
a w e akly dom in ant strategy equilibrium. ¥
3. Consider a 2 pla yer game with pure strategies for each player that can be
represen ted by a × m atrix. Assum e that for each pla yer no two pa yo ffs
in the matrix are the sam e.
(a) Show that if =2and the game has a unique pure strategy Nash
equilib riu m then this is the unique strategy profile that survives IESDS.
Answ er: Consider a general 2 × 2 game as follows,
Player 1
Play er 2
2
2
1
1
1
2
1
2
1
2
1
2
and assume without loss of generalit y that (
1
2
) is the unique pure
strategy Nash equilibrium.
1
Two statements are true: first, because
(
1
2
) is a Nash equilibrium and no two pa yoffs are the same for
each player then
1
1
and
2
2
.Second,because(
1
2
) is
not a Nash equilibrium then
1
1
and
2
2
cannot hold to-
gether (otherwise it w ould hav e been another Nash equilibrium ). These
1
The term “w ithou t loss of generality” me ans that we are choosing one particular strategy pro file bu t th e re is
nothing sp ecial ab out it an d we could have chosen any one of the others using the sam e argument.
5. Pinning Down Beliefs: Nash Equilibrium 63
t wo statemen ts imply that either ()
1
1
and
1
1
} in which
case
1
is dominated by
1
,or()
2
2
and
2
2
in which
case
2
is strictly dom inate d by
2
. This implies that either
1
or
2
(or both) will be elim ina ted in the first round of IESDS, and from the
fact that
1
1
and
2
2
it follo w s that if only one of the strate-
gies wa s removed in the first round of IESDS then the remaining one
will be remo ved in the second and finalround,leaving(
1
2
) as the
unique strategy that survives IESDS. ¥
(b) Show that if =3and the game has a unique pure strategy equilibrium
then it ma y not be the only strategy profile that survives IESDS.
Answ er: Cons ider this following game :
Play er 1
Play er 2
7 6 3 0 6 5
1 3 4 4 0 2
8 7 2 1 5 8
Notice that for both players none of the strategies are strictly dominated
implying that IESDS does not restrict any strategy profile survives
IESD S. Ho wever, th is game has a unique N ash equilibrium: ( ).
¥
4. Splitting Pizza: You and a friend are in an Italian restaurant, and the ow ner
offers both of you an 8-slice pizza for free under the follo w ing condition. Eac h
of y ou m ust simultaneously announce how man y slices you w ould lik e; that
is, each p layer ∈ {1 2} name s his desired am ount of pizza, 0 ≤
≤ 8.
If
1
+
2
≤ 8 then the play ers get their demands (and the owner eats an y
lefto ver slices). If
1
+
2
8, then the play ers get nothing. Assume that
y ou eac h care only about how m uc h pizza you individually consume, and the
more the better.
(a) Write out or graph each player’s best-response correspondence.
64 5. Pinning Down Beliefs: Nash Equilibrium
Answ er: Restrict attention to integer demands (more on contin uous
demands is belo w). If pla yer demands
∈ {0 1 7} then ’s best
response is to demand the complemen t to 8 slices. If asks for more
then both get nothing wh ile if asks for less then he is leaving some
slices unclaim ed . If instead player demands
=8then pla yer gets
nothing regardless of his request so any demand is a best response. In
summ ary,
(
)=
(
8 −
if
∈ {0 1 7}
{0 1 8} if
=8
Note: if the pla yers ca n ask for amounts that ar e not restricted to
integers then the same logic applies and the best response is
(
)=
(
8 −
if
∈ [0 8)
[0 8] if
=8
¥
(b) What outcome s can be supported as pur e-strateg y Nash equilibria?
Answ er: It is easy to see from the best response correspondence that
any pair of deman d s that add up to 8 will be a Nash equilib rium, i.e.,
(0 8) (1 7)(8 0). Ho wev er, there is another Nash equilibrium: (8,8)
in w h ich both players get n othin g. It is a Nash equilibriu m because
given that each player is asking for 8 slices, the other player gets noth-
ing regardless of his request, hence he is indifferent bet ween a ll of h is
requests including 8.
Note: The pair
=8and
= where ∈ {1 27} is not a Nash
equilibrium because ev en thou gh player is pla y ing a best response to
,player is not playing a best response to
because b y demanding
8 play er received noth ing, but if he instead dem an ded 8 − 0 then
he would get those amoun t of slices and get something. ¥
5. Pu blic Good Contribution : Th ree players live in a town and each can
c h oose to contribu te to fund a street lamp. T h e value of having the street
5. Pinning Down Beliefs: Nash Equilibrium 65
lam p is 3 for eac h player and the value of not having one is 0.TheMayor
asks eac h pla yer to either contrib ute 1 or nothing. If at least two pla yers
con trib ute then the lam p will be erected. If one or less people con tribu te
then the lamp will not be erected, in which case an y person wh o contribu ted
will not get their mo ney back.
(a) Write out or graph each player’s best-response correspondence.
Answ er: Consider pla y er with beliefs about the choice s of pla yers
and . If neither nor contribute then play er does not w ant to
contribute because the lamp would not be erected and he would lose
his con tribution. Similarly, if both and con tribute then pla yer does
notwanttocontributebecausethelampwouldbeerectedwithouthis
con tribution so he can “free ride” on their contributions. The remaining
cases is where only one of the players and contribute, in which case b y
contributin g 1 player receive s 3, while by not contributing he receiv es
0, and hen ce con tributing is a best response. In sum m ary,
(
)=
(
0 if
=
1 if
6=
(b) What outcome s can be supported as pur e-strateg y Nash equilibria?
Answ er: The best response corresponden ce described in (a) above im-
plies that there are two kinds of Nash equilib ria: one kind (which is
unique) is where no pla yer contributes, and the other kind has t wo of
the three play ers con trib uting and the third free riding . Hence, either
the lamp being erected with two players co ntributing or the lamp not
being erected with no pla yer contribu ting can be supported as Nash
equilib r ia . ¥
6. Hawk-Dov e: The follo wing game has been widely used in evolutionary biol-
ogy to understand how “fighting” and “display” strategies b y animals could
coexist in a population. For a typical Ha wk-Do ve game there are resources to
66 5. Pinning Down Beliefs: Nash Equilibrium
be gained (i.e. food, mates, territories, etc.) denoted as .Eachoftwoplayers
can c hooses to be aggressive, called “Ha wk ” (), or can be compromising,
called “Dove” (). If both players choose then they sp lit the resources,
butloosesomepayoff from inju ries, den o ted as . Assum e that
2
.If
both choose then they split the resources, but engage in som e display of
po wer that a display cost ,with
2
. Fina lly, if player chooses w h ile
ch ooses ,then gets all the resources while leav es with no benefits and
no costs.
(a) Describe this gam e in a matrix
Answ er:
Player 1
Play er 2
2
−
2
− 0
0
2
−
2
−
¥
(b) Assume that =10, =6and =4. What outcomes can be supported
as pure-strategy Nash equilibria?
2
Answ er: The game is:
Play er 1
Play er 2
−1 −1 10 0
0 10 1 1
and the t wo strategy profiles that can be supported as pure strategy
Nash equilibria are ( ) and ( ), leading to outcom es (10 0) and
(0 10) respectively. ¥
2
In the evolutio n a r y bi o lo gy litera tu re , th e a n a ly sis pe rfo rmed i s o f a very different nature. Instead of considering
the Nash equilibriu m an a ly s is o f a sta tic gam e , the a nalysis is a d ynamic a n a ly sis whe re succ es sful stra te g ie s
“replicat e ” in a larg e p opu la tio n . This a n a ly s is is p a rt o f a met h od o lo g y c a ll ed “evolu t io n a r y g a me th e or y.” For
more on this see Gintis (2 000).
5. Pinning Down Beliefs: Nash Equilibrium 67
7. The player Tragedy of the Commons: Suppose there are pla y ers in
the Tragedy of the Commons example in section 5.2.2.
(a) Find the N ash equilibrium of this g am e. H ow does affect the Nash
outcome?
Answ er: The analysis in section 2 concluded that in the -player game
the best response of pla yer is given b y
(
−
)=
−
P
6=
2
First, let’s consider a symm etric Nash equilibrium wh ere eac h player
c hooses the same level of consum ption
∗
. Because the best response
must hold for each and they all c h oose the same level
∗
then in the
Nash equilibrium the best response reduces to,
∗
=
− ( − 1)
∗
2
or,
∗
=
+1
The wa y in whic h affects the outcome is that first, as there are more
firm s, eac h will consum e less clean air. Second, as there are more firms,
the sum of clean air consumed b y the firms is
−1
, whic h increases with
.
It is more subtle to show that there cannot be other Nash equilibria. To
show this we will sho w that conditional on whatever is c ho sen by all but
t wo players, the two players must ch oose th e same amou nt in a Nash
equilibrium . Assume that there is another asymmetric Nash equilibrium
in which t wo players, and , choose two differen t equilibrium levels
∗
6=
∗
.Let =
P
6=
∗
be the sum of all the other equilibrium
c ho ices of the players who are not or . Because we assumed that this
is a Nash equ ilibrium , the best response function of both and must
hold simultaneously, that is,
∗
=
−
−
∗
2
(5.1)
68 5. Pinning Down Beliefs: Nash Equilibrium
and
∗
=
−
−
∗
2
(5.2)
If we substitute (5.2) into (5.1) w e obtain,
∗
=
−
−
−−
∗
2
2
which implies that
∗
=
−
3
.Ifwesubstitutethisbackinto(5.2)we
obtain,
∗
=
−
−
−
3
2
=
−
3
=
∗
,
which con tra dicts the assumption w e started with, that
∗
6=
∗
. Hence,
the unique Nash equilibrium has all the players c hoosing the same level
∗
=
+1
. ¥
(b) Find the socially optimal outco m e with players. How does affect
this outcome?
Answ er: The socially optimal outcome is found m y maximizing,
max
(
1
2
)
X
=1
ln(
)+ ln( −
X
=1
)
The first order conditions for this problem are,
1
−
−
P
=1
=0for =1 2 .
Just as for the analysis of the Nash equilibrium in part (a), the solution
here is also symmetr ic. Therefore the optimal solution,
,canbefound
using the followin g equa tion :
1
−
−
=0,
or,
=
2
, and the socially optimal total consum ptio n of clean air w ill
be equal to
2
regardless of the number of play ers. This implies that the
socially optimal solution is for the players to equally divide up half of
the clean air. ¥

5. Pinning Down Beliefs: Nash Equilibrium 69
(c) Ho w does the N ash equilibrium outco me compare to the socially effi-
cient outcome as approaches infinit y?
Answ er: The Nash equilibrium outcome alw ays has the firms consume
too m uch clean air as compared to the total
2
amount that social opti-
mality requires. Furthermore, as approac hes infinity the Nash levels of
consumption approach the total amoun t of clean air and the payoffs
of the players approaches −∞. ¥
8. The firm Cournot M odel: Suppose there are firms in the Cournot
oligopoly model. Let
denote the quantity produced by firm ,andlet
=
+···+
denote the aggregate production. Let () denote the mark et
clearing price (when demand equals ) and assume that inv erse demand
function is given b y ()= − (where ). Assume that firms ha ve
no fixed cost, and the cost of producing quantity
is
(all firmshavethe
same mar gin al cost, and assume that ).
(a) Model this as a Norm al form game
Answ er: The pla y ers are = {1 2 },eachplayerchooses
∈
where the strategy sets are
=[0 ∞) for all ∈ ,andthepayoffsof
each pla yer are given b y,
(
−
)=
⎧
⎪
⎪
⎨
⎪
⎪
⎩
( −
P
=1
)
−
if
P
=1
−
if
P
=1
≥
¥
(b) What is the Nash (Cournot) Equilibrium of the game where firms c hoose
their quantities simultaneously?
Answ er: Let’s begin by assuming that there is a symm etric “inter ior
solution” where eac h firm ch ooses the same positive quantit y as a Nash
equilibr iu m , and then w e will show that this is the only possible Nash
70 5. Pinning Down Beliefs: Nash Equilibrium
equilib riu m. Because each firm maximizes
(
−
)=( −
X
=1
)
−
,
the first order condition is
−
X
6=
− 2
− =0
which yields the best response of play er to be
(
−
)=
−
P
6=
−
2
.
Imposing symm etry in equilibrium implies that all best response con-
ditions will hold with the same values
∗
=
∗
for all ∈ ,andcanbe
solved using the best response function as follows,
∗
=
− ( − 1)
∗
−
2
,
which yields
∗
=
−
+1
It is more subtle to show that there cannot be other Nash equilibria. To
show this we will sho w that conditional on whatever is c ho sen by all but
t wo players, the two players must ch oose th e same amou nt in a Nash
equilibrium . Assume that there is another asymmetric Nash equilibrium
in which two players, and , choose two different equilibrium quantities
∗
6=
∗
.Let =
P
6=
∗
be the sum of all the other equilibrium
quantity choices of the players who are not or . Because we assumed
that this is a Nash equilibrium, the best response function of both and
m u st hold simultaneo usly, that is,
∗
=
−
−
∗
−
2
(5.3)
and
∗
=
−
−
∗
−
2
(5.4)
5. Pinning Down Beliefs: Nash Equilibrium 71
If we substitute (5.4) into (5.3) w e obtain,
∗
=
−
−
−−
∗
−
2
−
2
which implies that
∗
=
−−
3
. If we substitute this back into (5.4) w e
obtain,
∗
=
−
−
−−
3
−
2
=
−
−
3
=
∗
,
which contradicts the assumption we started with, that
∗
6=
∗
. Hence,
the unique Nash equilibrium has all the players c hoosing the same level
∗
=
−
+1
. ¥
(c) What happens to the equilibrium price as approaches infinity? Is this
familiar?
Answ er: First consider the total quantity in the Nash equilibrium as
afunctionof,
∗
=
∗
=
( − )
+1
and the resulting limit pric e is
lim
→∞
(
∗
) = lim
→∞
µ
−
( − )
+1
¶
= .
Thismeansthatasthenumberoffirms gro w, the Nash equilibrium
price will also fall and will approach the marginal costs of the firms as
the number o f firms gro w s to infinit y. Th ose familiar with a stan d ard
econom ics class kno w that in perfect competition price will equal mar-
ginal costs, which is what happens here when approaches infinit y. ¥
9. Tragedy of the Ro ommates: You and your −1 roommates each hav e 5
hours of free time you could spend cleaning your apartment. You all dislike
cleaning, but you a ll like having a clean room: each person’s pa yoff is the
72 5. Pinning Down Beliefs: Nash Equilibrium
total hours spent (b y everyone) cleaning, min us a nu mber times the hours
spent (individu a lly) cleanin g. That is,
(
1
2
)=− ·
+
X
=1
Assum e every o ne c h ooses simultaneously how much time to spend cleaning.
(a) Find the Nash equilibrium if 1.
Answ er: The pay off function is linear in one’s o wn time spen t
and
in the tim e spent b y the other roommates
, an d we can rew rite the
pa y off function as
(
−
)=
−
+
X
6=
Consid erin g this pa yo ff function, if 1 then every additional amou nt
of time that spend s cleaning giv es him an extra payoff of (1−)0 so
that each player would choose to spend all the 5 hours cleaning. Note
that using a first-order condition w o uld not work here because taking
thederivativeof
(
−
) with respect to
will just yield 1 − =0
which is not true for 1. This implies that there is a “corner” solution
in the range
∈ [0 5], in this case the Nash equilibrium is at the corner
∗
=5for all =1 2 . ¥
(b) Find the Nash equilibrium if 1.
Answ er: Similarly to (a) above, every ad ditional am ount of time
that spends cleaning giv es him an extra pa yoff of (1 − )0,so
that eac h player would choose to spend no time cleaning and the Nash
equilib r iu m is
∗
=0for all =1 2 . ¥
(c) Set =5and =2. Is the Nash equilibrium Pareto efficien t? If not,
can y ou find an outcome where everyone is better off than at the Nash
equilib riu m outcome?
Answ er: Follo wing the analysis in part (b), the unique Nash equilib-
rium is where ev eryone c hooses to spend no time cleaning and ev eryone’s

5. Pinning Down Beliefs: Nash Equilibrium 73
pa y off is equal to zero. Consider th e ca se w h ere everyone is someh ow
forced to choose
=1.Eachplayer’spayoff will be
(
−
)=
−
+
X
6=
=1− 2 × 1+4× 1=3 0
so that all the players will be better off if they all chose
=1.Infact,
eac h amou nt of time 0 that pla yer c h ooses to clean cause him
a person al loss of − 2 = , but increases the pa yoff of eac h of the
other players by . Hence, if w e can get eac h pla yer to increase his time
cleaning by ,thisyieldsanincreaseofvalueforeachplayerthatequals
his o w n loss, but the former is multiplied by the number of players.
Hence, the best sym metr ic outcome is when each player c hooses
=5.
¥
10. Synergies: Two division manag ers can invest time and effort in creating a
better working relationship. Eac h in vests
≥ 0, and if both invest more then
both are better off, but it is costly for each manager to in vest. In particular,
the payoff function for play e r from effort lev els (
) is
(
)=( +
)
−
2
.
(a) What is the best response correspondence of each pla yer?
Answ er: If player believe s that pla yer chooses
then ’s first order
optim ality conditio n for maxim izin g his payoff is,
+
− 2
=0
yielding the best response function,
(
)=
+
2
for all
≥ 0
¥

74 5. Pinning Down Beliefs: Nash Equilibrium
(b) In what way are the best response correspondences different from those
in the Courn ot game? Why?
Answ er: Here the best response function of pla yer is increasing in
the cho ice of player wherea s in the Cournot model it is decreasing in
thechoiceofplayer. This is because in this game the choices of the
t wo players are strateg ic complements while in the Cournot game they
are strategic substitutes. ¥
(c) Find the Nash equilibrium of this game and argue that it is unique.
Answ er: We solve two equation s with t wo unk now ns,
1
=
+
2
2
and
2
=
+
1
2
,
which yield the solution
1
=
2
= . It is easy to see that it is uniqu e
because it is the only poin t at wh ich these t wo best response functions
cross. ¥
11. Wasteful Shipping Costs. Consider t wo coun tries, and each with a
monopolist that owns the only coal mine in the coun try, and it produces coal.
Let firm 1 be the one located in country ,andfirm 2 the one in country
.Let
∈ {1 2} and ∈ { } denote the quantit y that firm sells in
coun try . Consequ ently, let
=
+
be the total quantit y produced by
firm ∈ {1 2},andlet
=
1
+
2
be the total quan tity sold in cou ntry
∈ { }. The demand for coal in coun tries and is given respectively
by ,
=90−
∈ { }
and the costs of production for eac h firm is giv e n by,
(
)=10
∈ {1 2}
(a) Assume that the coun tries do not ha ve a trade agreement and, in fact,
imports in both countries are prohibited. This implies that
2
=
1
=0
is set as a political constraint. Wh at quantities
1
and
2
will both
5. Pinning Down Beliefs: Nash Equilibrium 75
firm s produce?
Answ er: Eac h firm is a monopolist in its ow n coun try. Let and maxi-
mizes,
max
≥0
(90 −
)
− 10
where either =1and = or =2and = (so that
2
=
1
=0is set by assumption.) The first order maximization condition is
90 − 2
− 10 = 0, which yields
1
=
2
=40 The pay off for each firm
is 1 600. ¥
Now assume that the two coun tries sign a free-trade agreem ent that
allows foreign firms to sell in their coun tr ies without any tariffs. There
are, ho wever shipping costs. If firm sells quantity
in the foreign
country (i.e., firm 1 selling in or firm 2 selling in ) then shipping
costs are equal to 10
. Assume further that each firm chooses a pair of
quantities
simultaneo u sly, ∈ {1 2} so that a profile of actions
consists of four quantity c hoices.
(b) Model this as a normal form game and fin d a Nash equilibriu m of the
game y ou described. Is it unique?
Answ er: This game has tw o play ers, ∈ {1 2}, eac h ch oosing a strategy
that consists of two non -n egative quan tities, (
) ∈ R
2
+
,andthe
pa y off ofthetwoplayersaregivenby,
1
(
1
1
2
2
)=(90−
1
−
2
)
1
+(90−
1
−
2
)
1
− 10(
1
+
1
) − 10
1
2
(
1
1
2
2
)=(90−
1
−
2
)
2
+(90−
1
−
2
)
2
− 10(
2
+
2
) − 10
2
where the first term is the firm’s reve nue in marke t , the second is the
revenue in market , the third is the total production cost and the last
is the shippin g cost. Given beliefs (
2
2
) about what firm 2 chooses
to produce, firm 1’s optimization requires two partial derivative s with
76 5. Pinning Down Beliefs: Nash Equilibrium
respect to
1
and
1
as follo ws,
1
(
1
1
2
2
)
1
=90−
2
− 2
1
− 10 = 0
1
(
1
1
2
2
)
1
=90−
2
− 2
1
− 20 = 0
whichinturnleadtothetwopartsoffirm 1’s best response function,
3
1
=
80 −
2
2
(5.5)
1
=
70 −
2
2
(5.6)
It is easy to see that the objectiv e of firm 2 is symmetric to that of firm
1 and hence w e can directly write do wn firm 2’s best responses as,
2
=
70 −
1
2
(5.7)
2
=
80 −
1
2
(5.8)
The Nash equilibrium is solv ed b y finding a profile of strategies (
1
1
2
2
)
for whic h (5.5), (5.6), (5.7) and (5.8) all hold simultaneou sly. From (5.5)
and (5.7) w e obtain
1
=30and ,
2
=20. Sim ila rly, from (5.6) and
(5.8)weobtain
1
=20and ,
2
=30.Thepayoff of each firm s would
be equal to 1 300.
Now assume that before t he game yo u described in (b) is p layed, the
research department of firm 1 disco v ered that shipping coal with the
current ships causes the release of pollutants. If the firm would disclose
this report to the World-Trade-O rgan ization (WT O) then the WTO
w ould prohibit the use of the current ships. Instead, a new shipping
3
Because the payoff function has no interactions b etween the m arkets (i.e., it is separable in the two m arkets
so tha t there a re no interactions throu gh the cost function) then
1
depend s only on
2
and
1
depends only
on
2
(and vice versa for firm 2). If costs were not linear then this would not b e the case and the solution would
involve solving four equations wit four unknowns simultaneously.

5. Pinning Down Beliefs: Nash Equilibrium 77
tec hnology would be offered that w ould increase shipping costs to 40
(instead of 10
as abo ve).
(c) Would firm 1 be willing to release the information to the WT O ? Justify
y our answ er with an equilibrium analysis.
Answ er: To answer this w e need to solv e the Nash equilibrium with the
more expensive shipping tec hnology and compare the profits to that of
the curren t cheaper technology. We know that a monopolist (or compet-
itive firm ) would never prefer a m ore expensiv e tec hnology to a cheaper
one, but here there may be interesting strategic effects: the more ex-
pensive shipping technology will dampen competition. The new pa y o ff
functions are
1
(
1
1
2
2
)=(90−
1
−
2
)
1
+(90−
1
−
2
)
1
− 10(
1
+
1
) − 40
1
2
(
1
1
2
2
)=(90−
1
−
2
)
2
+(90−
1
−
2
)
2
− 10(
2
+
2
) − 40
2
and follo w ing the same argumen ts in part (b) above, the four equations
that will define the best responses of both firms are,
1
=
80 −
2
2
(5.9)
1
=
40 −
2
2
(5.10)
and,
2
=
40 −
1
2
(5.11)
2
=
80 −
1
2
(5.12)
From (5.9) and (5.11) we obtain
1
=40and ,
2
=0. Similarly, from
(5.10) and (5.12) w e obtain
1
=0and ,
2
=40. The pay off of each
firm s would be equal to 1 600, as w e calculated in part (a) above. Hence,
the firm wo uld lik e to disclose the informa tion and let the WT O impose
abanthatwouldeffectively kill cross-border competition. ¥

78 5. Pinning Down Beliefs: Nash Equilibrium
12. Asym m e tric Be rtrand : Consider the Bertrand game with
1
(
1
)=
1
and
2
(
2
)=2
2
,demandequalto =100− ,andwherefirm s m ust c hoose
prices in increments of one cen t. We have seen in section ?? that one possible
Nash equilibriu m is (
∗
1
∗
2
)=(199 200).
(a) Sho w that there are other Nash equilibria for this game.
Answ er: Another Nash equilib rium is (
0
1
0
2
)=(150 151)In this
equilib r iu m firm 1 fulfills market demand at a price of 1.50 and has no
incentive to cha ng e the price in eith er direction. Firm 2 is indifferen t
between the curr ent price and any higher price, and strictly prefers it
to lower prices. ¥
(b) How man y Nash equilibria does this game ha ve?
Answ er: There are 100 Nash equilibria of this gam e starting with
(
1
2
)=(100 101) and going all the w a y up with one-cent increases
to (
∗
1
∗
2
)=(199 200). The same logic explains why eac h of these is
a Nash equilib riu m. ¥
13. Com parativ e E conom ics: Two high tech firms (1 and 2) are considering
a joint venture. Each firm can in vest in a no vel techno logy, and can c hoose
a level of inv estm ent
∈ [0 5] at a cost of
(
)=
2
4
(think of
as how
many hours to train employees, or how much capital to buy for R&D labs).
The rev enue of each firm depends both on its investm ent, and of the other
firm ’s investmen t . In particular, if firm and choose
and
respectively,
then the gross revenue to firm is
(
)=
⎧
⎪
⎨
⎪
⎩
0 if
1
2 if
≥ 1and
2
·
if
≥ 1and
≥ 2
(a) Write do wn mathematically, and draw the profitfunction(gross rev-
enue min u s costs) of firm as a function of
for three cases: ()
2,
()
=2,and()
=4
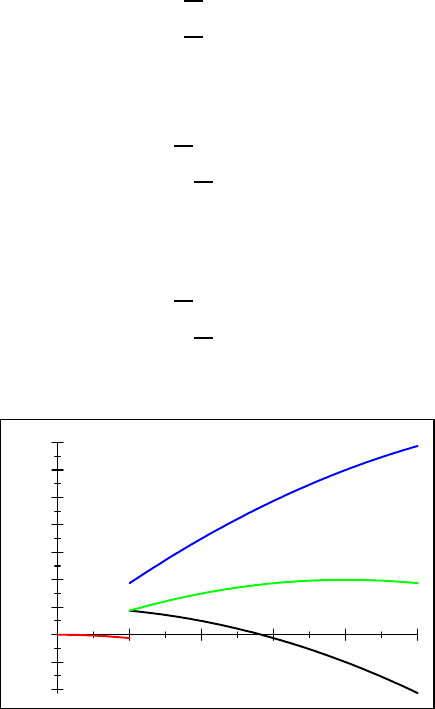
5. Pinning Down Beliefs: Nash Equilibrium 79
Answ er: For the case where
2 the pa yoff (profit) function of firm
is,
(
)=
(
0 −
2
4
if
1
2 −
2
4
if
≥ 1
for the case where
=2the payoff function of firm is,
(
)=
(
0 −
2
4
if
1
2
−
2
4
if
≥ 1
and for the case where
=4the payoff function of firm is,
(
)=
(
0 −
2
4
if
1
4
−
2
4
if
≥ 1
The three profit functions are depicted in the following figure:
1 2 3 4 5
-4
-2
0
2
4
6
8
10
12
14
x
y
All three share the same profits in the range
∈ [0 1) which is the red
line. The blac k line depicts the rest of the pa yoff function for the case
of
2, the green line depicts the rest of the payoff function for the
case of
=2, and the blue line depicts the rest of the payoff function
for the case of
=4. ¥
(b) What is the best response function of firm ?
Answ er: It is easy to see (and calculate) that when
2 then firm
’s best response is to c h oose
=1,andwhen
4 then firm ’s best

80 5. Pinning Down Beliefs: Nash Equilibrium
response is to choose
=5(a “corner” solution.) When
=2then
firm ’s best response solves
max
∈[05]
2
−
2
4
and the first order optimality condition is 2−
2
=0which yield s
=4.
More generally, as
gro ws abov e 2 the best response of firm will grow
above 4 until it hits the corner solution of
=5. In the range in which
player ’s best response in between 4 and 5 he maximizes his pa y off
function which is,
max
∈[05]
−
2
4
and his best response is deriv ed form the first order condition
−
2
=0,
which yields,
(
)=2
.
It is easy to see that for any
∈ [2 25] the best response of firm
is within the range [4 5] and for any
25 thebestresponseof is
“stuc k” at the corner solutio n
=
˙
5. Hen ce, we can write down the
general best response functio n of firm as,
(
)=
⎧
⎪
⎨
⎪
⎩
1 if
2
2
if
∈ [2 25]
5 if
25
¥
(c)Itturnsoutthattherearetwoidentical pairs of suc h firm s (that is,
the techn ology above describes the situation for both pairs). One pair
in R ussia where coordination is hard to achiev e and business people
are v ery cautious, and the other pair in G erman y where coordination
is common and business people expect their partners to go the extra
mile. You learn that the R u ssia n firms are earning significa ntly less
profits than the German firms, despite the fact that their tec h nolog ies
are identical. Can you use Na sh equilibrium analysis to shed light on

5. Pinning Down Beliefs: Nash Equilibrium 81
this dilemm a? If so, be precise and use your previo us analy sis to do so.
Answ er: The best response function described in part (b) leads to two
Nash equilibria: in the first (
∗
∗
)=(1 1) and (
∗∗
∗∗
)=(5 5).In
the first Nash equilibriu m the profits of eac h firm are
∗
=175, wh ile
in the second Nash equilibrium
∗∗
=1875.Thisisanexamplewhere
“self fulfilling expectations” can lead to two Nash equilib ria, one with
high pay offsandonewithlowpayoffs. This is an e xample of a gam e
with strateg ic com plements (see page 93) wh ere the co m plem e ntarity
cause m ultiple equilibria. ¥
14. Negativ e Ad Campaigns: Each one of two political parties can choose
to buy time on commercial radio sho w s to broadcast negativ e ad campaign s
against their rival. These c hoices are made sim ultaneously. Due to gov ern-
ment regulation it is forbidden to buy more than 2 hours of negativ e campaign
time so that eac h part y cannot choose an amount of negative campaigning
abo v e 2 hours. Giv en a pair of c hoices (
1
2
),thepayoff of party is given
by the follow ing function :
(
1
2
)=
− 2
+
− (
)
2
(a) What is the normal form representation of this gam e?
Answ er: Tw o play ers = {1 2}, for eac h pla yer the strategy space is
=[0 2] and the pa yoff of play er is given by
(
1
2
)=
− 2
+
− (
)
2
. ¥
(b) What is the best response function for each part y?
Answ er: Each player maximizes
(
1
2
) resulting in the first order
optim ality condition 1+
− 2
=0resulting in the best response
function,
(
)=
1+
2
¥
(c) What is the pure strategy Nash equilibrium? is it unique?
82 5. Pinning Down Beliefs: Nash Equilibrium
Answ er: Solving the two best response functions simultaneou sly,
1
=
1+
2
2
and
2
=
1+
1
2
yields the Nash equilibrium
1
=
2
=1, and this is the unique solution
to these equation s imp lyin g tha t this is the un iqu e equ ilibr ium. ¥
(d) If the parties could sign a binding agreement on how much to campaign ,
what levels would they c hoose?
Answ er: Both parties would be better off if they can c hoose not to
spend mon ey on negative cam paigns. Th e payoffs for each player from
the N ash equilibrium solved in part (c) are
(1 1) = −1 while of they
agreed not to spend anything they eac h w ould obtain zero. This is a
varian t of the Prisoners’ Dilemma. ¥
15. Hotelling’s Con tin uous Model: Consider H ot ellin g’s m odel where the
citizens are a continuum of v oters on the interval =[− ], with uniform
distribution ().
(a) What is the best response of candidate if candidate is choosing
0.
Answ er: Pla y er ’s best response will depend on the position of
relative to the ch oice
1
2
. For example, if
= − ∈ [− 0) then any
choice
∈ (
) will guaran tee pla yer victory. This follow s because
player will get mor e than − ofthevotefromtheinterval(
)
on his “right” (it is more because
), and he will split the inner
interval (−
) with play er so that his total share of the vote is
− +
− (−)
2
=
2 +
−
2
while the total share of pla y er is the interval (− −) on his “left”
plus splitting the inner inte rval (−
),whichis,
= − − (−)+
− (−)
2
=
2 +
−
2
5. Pinning Down Beliefs: Nash Equilibrium 83
which imp lies that
and will win the vote. A symmetric argu-
ment works for an y choice
= ∈ (0].Theremainingcaseis
=0.
In this case if
6=
then play er gets less tan half the vote while
if
=
then pla yer gets half the v o te, making
=
the best
response to
=0. We conclude that the best response correspondence
is,
(
)=
⎧
⎪
⎨
⎪
⎩
(
−
) if
0
0 if
=0
(−
) if
0
¥
(b) Sho w that the unique Nash equilibrium is
1
=
2
=0.
Answ er: This follo w s imm ed iately from the best response correspon-
dence in part (a) abo ve: only at the pair (
)=(0 0) are both pla yers
pla y ing a best response to each other. ¥
(c) Sho w that for a general distribution (·) over [− ], the unique Nash
equilibrium is where is candidate c hooses the policy associated with the
median voter.
Answ er: This again follo ws from the analysis in part (a) above just
that instead of 0 being the poin t at which half the v ote is obtained, it
is the median vot er
∗
for which half the v ote is at or abo v e
∗
and half
thevoteisatorbelow
∗
.
4
¥
16. Ho tellin g ’s Price Com petition: Imagine a con tinuum of potential buy ers,
located on the line segment [0 1], with uniform distribution. (Hence, the
4
If th e d is tr ib u tion () is c ontinu ous the the re will be s o me
∗
such that (
∗
)=
1
2
and that will be the
median voter. If there are “jumps” in the distribution () then the median voter can b e som e
∗
for wh ich
(
∗
)
1
2
. For instance , if half th e p o p u la t io n is distr ib u te d Un ifo rmly on [−1 1] and the oth er half are all
locat e d at the point
∗
=
1
2
then
3
8
of the p op ulation are s trictly below
∗
,
1
8
of the p opulation are strictly ab ove
∗
,and
1
2
of the population is exactly at
∗
.Inthiscase
()=
1+
4
if − 1 ≤
1
2
3+
4
if
1
2
≤ ≤ 1
so that (
∗
)=
3
4
,but
∗
is still the median vote r.
84 5. Pinning Down Beliefs: Nash Equilibrium
“mass” or quan tit y of buyers in the interval [ ] is equal to − .) Imagine
two firm s, pla yers 1 and 2 whoarelocatedateachendoftheinterval(player
1 at the 0 point and player 2 at the 1 point.) Each player can c hoose its price
, and each customer goes to the v en dor who offers them the highest value.
Ho wev er, price alone does not determine the value, but distance is importan t
as w ell. In particular, each buyer who buys the product from pla yer has
anetvalueof −
−
where
isthedistancebetweenthebuyerand
vendor , and represen ts the transportation costs of buying from v e ndor .
Th us, buy er ∈ [0 1] buys from 1 and not 2 if −
1
−
1
−
2
−
2
,andif
buying is better than getting zero. (He re
1
= and
2
=1−. The buying
c h oice would be reversed if the inequality is rever sed.) Finally, assume that
thecostofproductioniszero.
(a) Assume that is v ery large so that all the customers will be serv ed by at
least one firm, and that some customer
∗
∈ [0 1] is ind i fferen t between
the t wo firm s. What is the best response function of each player?
Answ er: Because customer
∗
’s distance from firm 1 is
∗
and his
distance from firm 2 is 1 −
∗
, his indifference implies that
−
1
−
∗
= −
2
− (1 −
∗
)
which gives the equation for
∗
,
∗
=
1+
2
−
1
2
It follows that under the assumptions above, given prices
1
and
2
,the
demands for firms1and2aregivenby
1
(
1
2
)=
∗
=
1+
2
−
1
2
1
(
1
2
)=1−
∗
=
1+
1
−
2
2
Firm 1’s maxim ization problem is
max
1
µ
1+
2
−
1
2
¶
1

5. Pinning Down Beliefs: Nash Equilibrium 85
which yields the first order condition
1+
2
− 2
1
=0
implying the best response function
1
=
1
2
+
2
2
.
A symm etric analysis yields the best response of firm 2,
2
=
1
2
+
1
2
.
¥
(b) Assume that =1. What is the Nash equilibrium? Is it unique?
Answ er: If we u se the best response functions calculated in part (a)
above then we obtain a unique Nash equilibrium
1
=
2
=1,andthis
implies that
∗
=
1
2
so tha t each firm gets half the market. However,
when =1th en the utilit y of customer
∗
=
1
2
is −
1
−
1
2
=1−1−
1
2
=
−
1
2
, implying that he would prefer not to buy, and by contin uit y, an
in terval of customers around
∗
w ould also prefer not to buy. his violated
the assum p tions we used to calculate the best response functions.
5
So,
the analysis in part (a) is invalid when =1. It is therefore useful to
start with the monopoly case when =1and see how each firm would
have priced if the other is absen t. Firm 1 maxim izes
max
1
(1 −
1
)
1
wh ich yie lds the so lu t i on
1
=
1
2
so th at everyone in the in terval ∈
[0
1
2
] wished to buy from firm 1 and no other customer w ould buy. By
symm etry, if firm 2 w ere a monopoly then the solution w o uld be
2
=
1
2
so that everyone in the interval ∈ [
1
2
1] would buy from firm 2 and no
other custom er would buy. But this implies that if both firm s set their
5
We need ≥ 15 for c u sto mer
∗
=
1
2
to be just indifferent between buying and not b uying when
1
=
2
=1.
All the other customers will strictly prefer buying.

86 5. Pinning Down Beliefs: Nash Equilibrium
monopoly prices
1
=
2
=
1
2
then eac h wou ld maxim ize profits ignoring
the other firm,andhencethisisthe(trivially)uniqueNashequilibrium.
¥
(c) No w assume that =1and that the transportation costs are
1
2
,so
that a buy er buys from 1 if a nd only if −
1
−
1
2
1
−
2
−
1
2
2
.
Write the best response function of each player and solv e for the Nash
Equ ilibrium .
Answ er: Lik e in part (a), assum e that cu stom er
∗
’s distance from
firm 1 is
∗
and his distance from firm 2 is 1 −
∗
, and he is indifferen t
between buying from either, so his indifference implies that
−
1
−
1
2
∗
= −
2
−
1
2
(1 −
∗
)
which gives the equation for
∗
,
∗
=
1
2
+
2
−
1
It follows that under the assumptions above, given prices
1
and
2
,the
demands for firms1and2aregivenby
1
(
1
2
)=
∗
=
1
2
+
2
−
1
1
(
1
2
)=1−
∗
=
1
2
+
1
−
2
Firm 1’s maxim ization problem is
max
1
µ
1
2
+
2
−
1
¶
1
which yields the first order condition
1
2
+
2
− 2
1
=0
implying the best response function
1
=
1
4
+
2
2
.

5. Pinning Down Beliefs: Nash Equilibrium 87
A symm etric analysis yields the best response of firm 2,
2
=
1
4
+
1
2
.
The Nash equilibriu m is a pair of price s for which these two best re-
sponse functions hold sim ultaneously, which yields
1
=
2
=
1
2
,and
∗
=
1
2
. To verify th at this is a Nash equilibrium notice th at for cus-
tomer
∗
, the utility form buying from firm 1 is −
1
−
1
2
=1−
1
2
−
1
2
=0
implying that he is indeed indifferent between buying or not, whic h in
turn implies that eve ry other customer prefer buying ov er not buying.
¥
(d) Follow ing your analysis in (c) above, imagine that transportation costs
are
,with ∈ [0
1
2
]. Wha t h appens to the N ash equilibrium as
→ 0? What is the intuition for this result?
Answ er: Usin g the assumed indifferent customer
∗
, his indifference
imp lies that
−
1
−
∗
= −
2
− (1 −
∗
)
−
1
− = −
2
− (1 − )
which gives the equation for
∗
,
∗
=
1
2
+
1
2
(
2
−
1
)
It follows that under the assumptions above, given prices
1
and
2
,the
demands for firms1and2aregivenby
1
(
1
2
)=
∗
=
1
2
+
1
2
(
2
−
1
)
1
(
1
2
)=1−
∗
=
1
2
+
1
2
(
1
−
2
)
Firm 1’s maxim ization problem is
max
1
µ
1
2
+
1
2
(
2
−
1
)
¶
1

88 5. Pinning Down Beliefs: Nash Equilibrium
which yields the first order condition
1
2
+
2
2
−
1
=0
implying the best response function
1
=
2
+
2
2
.
A symm etric analysis yields the best response of firm 2,
2
=
2
+
1
2
.
2
=
2
+
2
+
2
2
2
.
The Nash equilibriu m is a pair of price s for which these two best re-
sponse fu nctions ho ld simultaneously, whic h y ields
1
=
2
= ,and
∗
=
1
2
. From the analysis in (c) abo ve we know that for any ∈ [0
1
2
)
custom er
∗
will strictly prefer to buy o ver not buying and so will every
other customer. We see that as decreases, so do the equilibrium prices,
so that at the limit of =0the prices will be zero. The intu ition is that
the transportation costs cause firms 1 and 2 to be differen tiated, and
this “softens” the Bertrand competition bet ween the t wo firm s. When
the transportation costs are higher this implies that competition is less
fierce and prices are higher, and the opposite holds for lo wer transporta-
tion costs.¥
17. To v ote or not to vote: Two candidates, and , are running for ma y oral
election in a tow n with residen ts. A total of 0 residen ts support
candidate while the remainder = − support candidate .Thevalue
for each resident for having their candida te win is 4, for having him tie is 2,
and for having him lose is 0. Going to vote costs each resident 1
(a) Let =2and =1. Write down this game as a matrix and solv e for
the Nash equilib r ium.
Answ er: Thegameisbetweentheresidentsasthecandidatesseemnot

5. Pinning Down Beliefs: Nash Equilibrium 89
to pla y a role and the question is whether to v ote or not to v ote. Letting
denote “y es” v ote and denote “no” vote, the matrix representation
of this t wo player game is
Player 1
Play er 2
1 1 3 0
0 3 2 2
If both vote or both don’t v ote then there is a tie and the only difference
is the cost of v otin g. If only one v otes then his candidate wins and he
exerts the v o ting costs, while the other gains and expends nothing.
Voting is a dominant strategy so ( ) is the unique Nash equilib riu m.
¥
(b) Let 2 be an even number and let = =
2
. Find all the N ash
equilib r ia .
Answ er: Observe that ev e ryo ne v o ting is a Nash equilibriu m . Like in
part (a) there will be a tie and every pla yer’s pay off is 1, while if he
c h ose not to vote then his c andid ate will lose and his payoff will be
0, hence it is a Nash equilibrium. We no w show that no other profile
of strategies is a Nash equilib rium in three steps. Let
0
and
0
denote
the number of member of eac h group that plan on voting. ()Assume
that a n identical number of voters from each side v otes so that there
is a tie but some v oter s are not vo ting, that is,
0
=
0
2
.Inthis
case any one of the vo ters who is no t voting w ou ld prefer to devia te,
expend a voting cost of 1 and increase his pa yoff from2to3becausehe
would tip the ele ction . Hen ce , this cannot be a N ash equilibrium . ()
Now assume that the number of supporters of candidate is is at least
2morethanthatofcandidate,thatis,
0
≥
0
+2.(Asymmetric
argum ent will apply to the case of
0
≥
0
+2.) In this case any one of
the supporters who plans to v ote knows that his v ote is redundant,
and hence he w ould prefer not to v ote and sa ve the v oting costs. Hence,
this cannot be a Nash equilibrium . ()Nowassumethatthenumber
90 5. Pinning Down Beliefs: Nash Equilibrium
of supporters of candidate is is exactly 1 more than that of candidate
,thatis,
0
=
0
+1. (A symm etric argument will apply to the case
of
0
=
0
+1.) In this case an y one of the supporters who does not
plan to vote know s that his v ote can turn a loss into a tie, and hence
he wo uld prefer to v ote and c han ge the election giving him a pa yoff of 1
instead of 0. H ence , this too cannot be a Nash equilibrium. This covers
all the possible scenarios and shows that every one v oting is the unique
Nash equilibrium . ¥
(c) Assume now that the costs of voting are equal to 3. Ho w does y our
answer to (a)and(b)change?
Answ er: The tw o play er game is now
Play er 1
Play er 2
−1 −1 1 0
0 1 2 2
and the dominated strategy is voting, implying that the unique N ash
equilibr iu m is for the players not to v ote , ( ). A similar argument
to part (b) abov e sho ws that all pla yers not v oting is the unique Nash
equilib r iu m . ¥
18. P olitical Cam paigning: Two candidates are competing in a political race.
Each candidate can spend
≥ 0 on adds that reac h out to voters, whic h
in turn increases the probability that candidate wins the race. Giv en a pair
of spending c h oices (
1
2
), the probability that candidate wins is given
by
1
+
2
. If neither spends any resources then eac h wins with probability
1
2
.
Eac h candidate values winning at a pa y off of 0,andthecostofspending
is just
.
(a) Giv e n t wo spend lev els (
1
2
), write the expected pa yoff of a candidate

5. Pinning Down Beliefs: Nash Equilibrium 91
Answ er: Play er ’s payoff function is
(
1
2
)=
1
+
2
−
¥
(b) What is the function that represents eac h pla yer’s best response func-
tion?
Answ er: Pla y er 1 maximizes his pay off
1
(
1
2
) shownin(a)above
and the first order optimality condition is,
(
1
+
2
) −
1
(
1
+
2
)
2
− 1=0
and if w e use
1
(
2
) to denote pla yer 1’s best response function then
it explicitly solves the follo w ing equalit y that is derived from the first-
order condition,
[
1
(
2
)]
2
+2
1
(
2
)
2
+(
2
)
2
−
2
=0
Becau se this is a quadratic equation we can no t write an explicit best
response function (or correspondence). However, if we can graph
1
(
2
)
asshowninthefollowingfigure (the values correspond for the case of
=1).
0.2 0.4 0.6 0.8 1.0 1.2
-0.2
-0.1
0.0
0.1
0.2
0.3
0.4
s2
s1
Similarly w e can derive the symm et ric func tion for player 2. ¥

92 5. Pinning Down Beliefs: Nash Equilibrium
(c) Find the unique Nash equilibrium.
Answ er: The best response functions are symm etr ic mirror images and
have a symmetric solution where
1
=
2
in the unique Nash equilibr iu m .
We can therefore use an y one of the two best response functio ns and
replace both variables with a single variable ,
2
+2
2
+
2
− =0
or,
=
4
so that the uniqu e Nash equ ilibr iu m has
∗
1
=
∗
2
=
4
¥
(d) What happens to the Na sh equilib rium spending levels if increases?
Answ er: It is easy to see from part (c) tha t higher values of cause
the pla yers to spend more in equilibriu m . As the stak es of the prize rise,
it is mo re valuable to figh t over it. ¥
(e) What happens to the N ash equilibr iu m levels if pla yer 1 still values
winning at , but play er 2 values winning at where 1?
Answ er: N ow the two best response functions are not symm etric. The
best response function of player 1 rema ins as above, but that of pla yer
2willnowhave instead of ,
(
1
)
2
+2
1
2
+(
2
)
2
−
2
=0 ((BR1 ))
and
(
2
)
2
+2
1
2
+(
1
)
2
−
1
=0 ((BR2 ))
Subtracting (BR2) from (BR1) w e obtain,
1
=
2
,
which implies that the solution will no longer be sym m e tric and, more-
over,
2
1
which is in tuitive because no w pla y er 2 cares more about
the prize. Using
1
=
2
we substitute for
2
in (BR1) to obtain,
(
1
)
2
+2(
1
)
2
+
2
(
1
)
2
−
1
=0

5. Pinning Down Beliefs: Nash Equilibrium 93
which results in,
1
=
1+2 +
2
1+2 +
2
4
where both inequalities follow from the fact that 1.From
1
=
2
abovewehave
2
=
2
1+2 +
2
2
2
+2
2
+
2
=
4
where the ine quality fo llows from 1. ¥
94 5. Pinning Down Beliefs: Nash Equilibrium

This is page 95
Printer: Opaque
t
6
M ixed Strategies
1. Use the best response correspondences in the B attle of the Sexes game to
find all the Nash equilibria. (Follow the approac h used for the example in
section 6.2.3.)
Answ er: TheBattleoftheSexesgameisdescribedbythefollowingmatrix,
player 1
Player 2
2 1 0 0
0 0 1 2
Let denote the probabilit y that player 1 pla ys and let be the probability
that player 2 pla ys . The expected pa yoff of player 1 from playing is
1
( )=2 and of pla ying is
1
( )=1− . It is easy to see that is
better than if and only if 21 − ,or
1
3
. Hence, the best response
correspondence of play er 1 is:
1
()=
⎧
⎪
⎨
⎪
⎩
=1 if
1
3
∈ [0 1] if =
1
3
=0 if
1
3

96 6. Mixed Strategies
The best response of p layer 2 is derived a nalogou sly:
2
( )
2
( ) if
and only if 2(1 − ),or,
2
3
, implyin g that ,
2
()=
⎧
⎪
⎨
⎪
⎩
=1 if
2
3
∈ [0 1] if =
2
3
=0 if
2
3
It is now easy to see that there are three Nash equilibria: ( ) ∈ {(1 1) (
2
3
1
3
) (0 0)}.
¥
2. Let
be a mixed strategy of pla yer that puts positive weight on one strictly
dom inated pure strategy. Show that there exists a mixed strategy
0
that puts
no w eight on any dom inated pure strategy and that dom inates
.
Answ er: Let player hav e pure strategies
= {
1
2
} and let
be a pure strategy which is strictly dominated by
0
,thatis,
(
0
−
)
(
0
−
) for an y strategy profile of ’s opponents
−
.Let
=(
1
2
)
be a mixed strategy that puts some positiv e w eight
0 on
and let
0
be iden tical to
except that it puts weight 0 on
and div erts that w eight
over to
0
.Thatis,
0
=0and
0
0
=
0
+
,and
0
=
for all 6=
and 6=
0
. It follo ws that for all
−
,
(
0
−
)=
X
=1
0
(
−
)
X
=1
(
−
)=
(
0
−
)
because
(
0
−
)
(
0
−
) and the w a y in which
0
was constructed.
Hence,
is strictly dom ina ted by
0
. ¥
3. Consider the game used in section ?? as follows:
Play er 1
Player 2
5 1 1 4 1 0
3 2 0 0 3 5
4 3 4 4 0 3
6. Mixed Strategies 97
(a) Find a strategy different from (
2
()
2
()
2
()) = (0
1
2
1
2
) that
strictly dominates the pure strategy forplayer2.Arguethatyoucan
find an infin ite n u mber of suc h strategies.
Answ er: The expected pa yoff of any player in a m a trix game is con-
tinuous in the proba bilities of his mix ed strategy (because it is a lin-
ear fun ction of the probab ility weights), and hence if we “tweak” the
strategy (
2
()
2
()
2
()) = (0
1
2
1
2
) just a little bit then the pay-
offs will be the same for an y c h oice of pla yer 1. For exam ple, tak e
0
2
=(
0
2
()
0
2
()
0
2
()) = (0
4
10
6
10
). The expected pay o ff of pla yer
2from
0
2
against an y one of the three strategies of pla yer 1 are,
2
(
0
2
)=04 × 4+06 × 0=16 1=
2
( )
2
(
0
2
)=04 × 0+06 × 5=3 2=
2
( )
2
(
0
2
)=04 × 4+06 × 3=34 3=
2
( )
which shows that
0
2
strictly dom inates . It is therefore follows by the
continuit y of the expected payoff function that an y one of the infinitely
many mixed strategies that puts weights close to 0.5 on and the
remain ing pro ba bility on will dom inate .
1
¥
(b) Find a strategy differen t from (
1
()
1
()
1
()) = (0
1
2
1
2
) that
strictly dominates the pure strategy forplayer1inthegameremain-
ing after one stage of elimination. Argue that you can find an infinite
number of such strategies.
Answ er: This is an identical procedure as for part (a).
4. Monitoring: An emplo yee (pla yer 1) w h o w orks for a boss (play er 2) can
either w ork ( )orshirk(), while his boss can either monitor the employ e e
() or ignore him (). L ike most employee-boss rela tionship s, if th e em-
ployee is w orking then the boss prefers not to monitor, but if the boss is not
1
A m ore elegant way 0f writing this would b e to choose a m ixed strategy
0
2
=(0
1
2
+
1
2
− ) and show that
for sm all enough values of it follows t h a t
0
2
strictly dominates , a nd it fo llows th a t th e re ar e infinitely many
such values o f .
98 6. Mixed Strategies
monitorin g then the employee prefers to shirk. The game is represented in
the follo w ing matrix :
player 1
Play er 2
1 1 1 2
0 2 2 1
(a) Dra w the best response functions of each player.
Answ er: Let be the probability that pla yer 1 ch ooses and the
probability that player 2 c hooses . It follows that
1
( )
1
( )
if and only if 1 2(1 −),or
1
2
,and
2
( )
2
( ) if and only
if +2(1− ) 2 +(1− ),or
1
2
. It follo ws that for pla y er 1,
1
()=
⎧
⎪
⎨
⎪
⎩
=0 if
1
2
∈ [0 1] if =
1
2
=1 if
1
2
and for player 2,
2
()=
⎧
⎪
⎨
⎪
⎩
=1 if
1
2
∈ [0 1] if =
1
2
=0 if
1
2
Notice that these are iden tical to the best response functions for the
matchingpenniesgame(seeFigure6.3).¥
(b) Find the Nash equilibrium of this game. What kind of game does this
game remind yo u of?
Answ er: From the two best response correspondences the unique Nash
equilib r iu m is ( )=(
1
2
1
2
) and the game’s strategic forces are identical
to those in the Match ing Pennies game. ¥
5. Cops and Robbers: Player 1 is a police officer who must decide whether to
patrol the streets or to hang out at the coffee shop. His pa yoff from hang ing
out at the coffee shop is 10, while his pay off from p atrolling the streets
6. Mixed Strategies 99
depends on whether he catches a robber, who is pla yer 2. If the robber prowls
the streets then the police officer will catch him and obtain a payoff of 20.
If the robber stays in his hidea way then the officer’s payoff is 0. The robber
m u st choose between sta ying hidden or pro wling the street. If he stays hidden
then his payoff is 0, while if he wa lk s the street his pay o ff is (−10) if the officer
is patrolling the streets, and it is 10 if the officer is at the coffee shop.
(a) Write dow n the matrix form of this gam e.
Answ er: Let denote patrol and coffee shop for player 1, and is
the robber’s choice of pro w ling while is remaining hidden. Th e game
is therefore
player 1
Play er 2
20 −10 0 0
10 10 10 0
¥
(b) Dra w the best response functions of each player.
Answ er: Let be th e probability th at pla yer 1 chooses and the
probability that player 2 ch ooses . It follow s that
1
( )
1
( )
if and only if 2010,or
1
2
,and
2
( )
2
( ) if and only if
−10 +10(1− ) 0,or
1
2
.Itfollowsthatforplayer1,
1
()=
⎧
⎪
⎨
⎪
⎩
=0 if
1
2
∈ [0 1] if =
1
2
=1 if
1
2
and for player 2,
2
()=
⎧
⎪
⎨
⎪
⎩
=1 if
1
2
∈ [0 1] if =
1
2
=0 if
1
2
Notice that these are iden tical to the best response functions for the
matchingpenniesgame(seeFigure6.3).¥

100 6. Mixed Strategies
(c) Find the Nash equilibrium of this game. What kind of game does this
game remind yo u of?
Answ er: From the t wo best response correspondences the unique Nash
equilib r iu m is ( )=(
1
2
1
2
) and the game’s strategic forces are identical
to those in the Match ing Pennies game. ¥
6. Declining Industry: Consider tw o competing firms in a declining indus-
try that cannot support both firms profita bly. Each firm has three possible
choicesasitmustdecidewhetherornottoexittheindustryimmediately,at
the end of this quarter, or at the end of the next quarter. If a firm c h ooses
to exit then its payoff is 0 from that poin t on ward. Ev ery quarter that both
firm s operate yields each a loss equal to −1, and eac h quarter that a firm
operates alone yields a pa yoff of 2 For example, if firm 1 plans to exit at the
end of this quarter while firm 2 plans to exit at the end of the next quarter
then the payoffsare(−1 1) because both firms lose −1 in the first quarter
and firm 2 gains 2 in the second. The pay off for each firm is the sum of its
quarterly payoffs.
(a) Write dow n this game in matrix form.
Answ er: Let denote immediate exit, denote exit this quarter , and
denote exit next quarter.
Play er 1
Player 2
0 0 0 2 0 4
2 0 −1 −1 −1 1
4 0 1 −1 −2 −2
(b) Are there any strictly dominated strategies? Are there an y w eakly dom-
inated strategies?
Answ er: There are no strictly dominated strategies but there is a
w eakly dominated one: . To see this note that choosing both and
6. Mixed Strategies 101
with probability
1
2
eac h yields the same expected payoff as c hoos-
ing against or , and a higher expected pay off against and
hence
=(
()
( )
()) = (
1
2
0
1
2
) weakly dominates .The
reason there is no strictly domina ted strategy is that, starting with
,
increasing the weight on causes the mixed strategy to be w or se than
against , while increasing the w eig ht on causes the mixed strat-
egy to be w orse than against , implying it is impossible to find a
mixed strategy that strictly dominates . ¥
(c) Find the pure strategy Nash equilibria.
Answ er: Because is we ak ly dom ina ted , it is suspect of never being
a best response. A quic k observation should conv ince you that this is
indeed the case: it is never a best response to an y of the pure strategies,
and hence cannot be part of a pure strategy Nash equilibrium . Rem oving
fro m consid eration results in the reduced game:
Play er 1
Player 2
0 0 0 4
4 0 −2 −2
for whic h there are two pure strategy Nash equilibria, ( ) and ( ).
¥
(d) Find the unique mixed strategy Nash equilibr ium (hint: you can use
y o ur answer to (b) to mak e things easier.)
Answ er: We start by ignoring and using the reduced game in part
(c) b y assum ing that the w eakly do min ated strategy will never be
part of a Nash equilibrium . We need to fin d a pair of mixed strategies,
(
1
()
1
()) and (
2
()
2
()) that mak e both players indifferent
between and . For pla yer 1 the indifference equatio n is,
0=4
2
() − 2(1 −
2
())
which results in
2
()=
1
3
,andforplayer2theindifference equation
is symmetric, resulting in
1
()=
1
3
. Hence, the mixed strategy Nash

102 6. Mixed Strategies
equilib riu m o f the original gam e is (
()
( )
()) = (
1
3
0
2
3
).
Notice that at this Nash equilibrium, each player is not only indifferent
between and , but choosing giv es the sam e expected pa yoff of
zero. However, c hoosing with positiv e probabilit y cannot be part of
a mixed strategy Nash equilibrium. To pro ve this let player 2 play the
mixed strategy
2
=(
2
()
2
( )
2
()) = (
2
2
1 −
2
−
2
)
The strategy forplayer1isatleastasgoodas if and only if,
0 ≤ 2
2
−
2
− (1 −
2
−
2
)
or,
2
≥
1
3
. The strategy for player 1 is at least as good as if and
only if,
4
2
−
2
− 2(1 −
2
−
2
) ≤ 2
2
−
2
− (1 −
2
−
2
)
or,
2
≤ 1−3
2
.Butif
2
≥
1
3
(when is as good as )then
2
≤
1 − 3
2
reduces to
2
≤ 0, whic h can only hold when
2
=
1
3
and
2
=0(which is the Nash equ ilib rium w e found abo ve). A symm etric
argument holds to conclude that (
()
( )
()) = (
1
3
0
2
3
) is the
uniqu e mixed strategy Nash equilibrium. ¥
7. Grad School Competition: Twostudentssignupforanhonorsthesis
with a Professor. Eac h can in vest time in their o w n project: either no time,
oneweek,ortwoweeks(thesearetheonlythreeoptions).Thecostoftimeis
0 fornotime,andeachweekcosts1 unit of pa yoff. The more time a student
puts in the better their work will be, so that if one student puts in more time
than the other there will be a clear “leader”. If they put in the same amount
of time then their thesis projects will ha ve the same quality. The professor,
however, will give out only one “A” grade. If there is a clear leader then he
will get the A, while if they are equally good then the professor will toss a
fair coin to decide who gets the A grade. The other studen t gets a “B”. Since
both wish to con tinue to gra dua te sch ool, a gr ade of A is worth 3 wh ile a
grade of B is wo rth zero.
(a) Write dow n this game in matrix form.

6. Mixed Strategies 103
Answ er: Let denote no time, denote one w eek, and denote t wo
weeks. The matrix game is,
Player 1
Player 2
15 15 0 2 0 1
2 0 05 05 −1 1
1 0 1 −1 −05 −05
The pa y offs are deriv ed b y the fact that a tie is an equal c hance of
getting 3 so each player gets 1.5 in expectation. ¥
(b) Are there any strictly dominated strategies? Are there an y w eakly dom-
inated strategies?
Answ er: Eachoneofthethreestrategiescanbeastrictbestresponse:
is a best response to , is a best response to ,and is a best
response to . Hence, no strategy is strictly or weakly dominated . ¥
(c) Find the unique mixed strategy N ash equilib r ium.
Answ er: Let
=(
1 −
−
) denote a mixed strategy for
player . Because the game is symm etric it suffices to solve the indiffer-
ence condition s for one pla yer. For player to be indifferen t bet ween
and ,
15
=2
+05
− (1 −
−
)
and for him to be indifferent bet ween and ,
15
=
+
− 05(1 −
−
)
Solving these t wo equations with t wo unknowns yields
=
=
1
3
implying that the unique mixed strategy Nash equilibrium has the
pla yers mixing between all three pure strategies with equal probabilit y.
¥
8. Market en try: There are 3 firm s that are considering enter ing a new market.
The pa y off for each firm that enters is
150
where is the n umber of firms
that en ter . The cost of entering is 62.

104 6. Mixed Strategies
(a) Find all the pure strategy Nash equilibria.
Answ er: The costs of entry are 62 so the benefits of entry m u st be at
leastthatforafirm to choose to enter. Clearly, if a firm believes the
other two are not entering then it wan ts to en ter, and if it believ es that
the other firm s are entering then it would sta y out (it w ould only get
50). If a firm believes that only one other firm is entering then it prefers
to enter and get 75. Hence, there are three pure strategy Nash equilibria
in which two of the three firms en ter and one stays out. ¥
(b) Find the symm etric mixed strategy equilibrium where all three players
enter with the same probability.
Answ er: Let be the probability that a firm enters. In order to be
willing to mix th e ex pected payoff of en tering must be equal to zero.
If a firm en ters then with pro bab ility
2
it will face two other en trants
and receive
=50− 62 = −12 with prob ab ility (1 − )
2
it will face
no other en tran ts and receive
=150− 62 = 88 and with probab ility
2(1 − ) it will face one other en trant and receive
=75− 62 = 13
Hen ce, to be willing to mix the expected pa yo ff must be zero,
2
+1−
2
(1 − )
2
88 + 2(1 − )13 −
2
12 = 0
which results in the qu ad ratic equation 25
2
− 75 +44=0,andthe
relevan t solution (between 0 and 1) is =
4
5
. ¥
9. Discrete all pay auction: In section 6.1.4 we introduced a v ersion of an all
pa y auction that work ed as follo ws: Eac h bidder submits a bid. The highest
bidder gets the good, but all bidders pay there bids.Consideranauctionin
which player 1 values the item at 3 while player 2 values the item at 5 Each
player ca n bid either 0 1 or 2. T he twist is that each pla yer pays his bid
regardless of wheth er he wins the good. If pla yer bids more than pla yer
then win’s the good and both pa y. If both players bid the sam e am ount
then a coin is tossed to determine who gets the good but again, both pay.

6. Mixed Strategies 105
(a) Write down the game in ma trix form. Which strategies survive IESDS ?
Answ er: Let denote zero, denote one, and denote tw o. The
matrix game is,
Player 1
Player 2
15 25 0 4 0 3
2 0 05 15 −1 3
1 0 1 −1 −05 05
The pa y offs are deriv ed b y the fact that a tie is an equal c hance of
winnin g so pla yer 1 gets 1.5 and pla yer 2 gets 2.5 in expectation. It is
easy to see that for play er 2, pla ying is dominated b y pla ying ,so
it is eliminated in the first stage of IESD S . In the second stage is
dominated b y for player 1 and we are left with the following reduced
game that survives IESDS,
Player 1
Play er 2
0 4 0 3
1 −1 −05 05
¥
(b) Find the Nash equilibria of this game.
Answ er: From the reduced game it is easy to see that there is no pure
strategy Nash equilibrium . Let
1
=(
1
1
) and
2
=(
2
2
)
denote the mixed strategies for the players in the reduced game. For
player 1 to be indifferen t bet ween and ,
0=
2
− 05(1 −
2
)
which yields
2
=
1
3
.Forplayer2tobeindifferent between and ,
4
1
− (1 −
1
)=3
1
+05(1 −
1
)

106 6. Mixed Strategies
which yields
1
=06. Thus, the unique mixed strategy Nash equilib-
rium has the pla yers mixing
1
=(
3
5
2
5
) and
2
=(
1
3
2
3
) in the reduced
game, or
1
=(
3
5
0
2
5
) and
2
=(0
1
3
2
3
) in the original game. ¥
10. Contin uous all pay auction: Consid er an all-pa y auction for a good w orth
1toeachofthetwobidders.Eachbiddercanchoosetooffer a bid from the
unit interval so that
=[0 1]. Players only care about the expected value
they will end up with at the end of the game (i.e., if a player bids 0.4 and
expects to win with probab ility 0.7 then his payoff is 07 × 1 − 04).
(a) Model this auction as a norm al-form game.
Answ er: There are t wo players, = {1 2}, eac h has a strategy set
=[0 1], and assuming that the players are equa lly lik ely to get the
good in case of a tie, the payoff to play er is given by
(
)=
⎧
⎪
⎨
⎪
⎩
1 −
if
1
2
−
if
=
−
if
(b) Sho w that this game has no pure strategy Nash Equilibrium.
Answ er: First, it cannot be the case that
=
1 because then each
player w o uld benefit from raising his bid b y a tiny amount in order to
win the auction and receive a higher payoff 1 − −
1
2
−
. Second,
it cannot be the case that
=
=1because each pla y er would prefer
to bid nothing and receiv e 0 −
1
2
. Last, it cannot be the case that
≥ 0 because then pla y er would prefer to lower his bid by
while still beating player and paying less money. Hence, there cannot
be a pure strategy Na sh equilib rium. ¥
(c) Sho w that this game cannot ha ve a Nash Equilibrium in which each
player is rando m izing over a finite number of bids.
Answ er: Assume that a Nash eq uilibriu m involves player 1 mixin g

6. Mixed Strategies 107
between a finite n um ber of bids, {
11
12
1
} where
11
≥ 0 is the
lowest bid,
1
≤ 1 is the highest,
1
1(+1)
andeachbid
1
is
bein g played with som e positive proba b ility
1
. Similarly assume that
player 2 is mixing between a finite number of bids, {
21
22
2
}
andeachbid
2
is being pla yed with som e positiv e probability
2
.()
First observe that it cannot be true that
1
2
(or the reverse by
symm etry). If it w er e the case then player 2 will win for sure when he
bids
2
and pay his bid, while if he reduces his bid b y some such that
1
2
− then he will still win for sure and pay less, cont radictin g
that pla y ing
2
was part of a Nash equilibrium . () Second observe
that when
1
=
2
then the expected pay off of pla y er 2 from bidding
2
is
2
=Pr{
1
2
}(1 −
2
)+Pr{
1
=
2
}(
1
2
−
2
)
=(1−
1
)(1 −
2
)+
1
(
1
2
−
2
)
=1−
2
−
1
2
≥ 0
where the last inequalit y follow s from the fact that
2
0 (he would
not play it w ith positive probability if the expected pa yoff were nega-
tive.) Let
0
2
=
2
+ where =
1
4
. If instead of bidding
2
player
2bids
0
2
then he wins for sure and his utility is
2
=1−
0
2
=1−
2
−
1
4
1 −
2
−
1
2
contradicting that playin g
2
was part of a Nash equilibriu m . ¥
(d) Consider mixed strategies of the follo wing form: Eac h play er chooses
and interval, [
] with 0 ≤
≤ 1 together with a cum u lative
distribution
() over the interval [
] (Alternatively y ou can think
of each player choosing
() over the interv al [0 1], with two values
and
suc h that
(
)=0and
(
)=1.)
i. Show that if two such strategies are a mixed strategy Nash equilib-
rium then it m ust be that
1
=
2
and
1
=
2
108 6. Mixed Strategies
Answ er: Assum e not. There are two cases: ()
1
6=
2
:With-
out loss assume that
1
2
. This means that there are values
of
0
1
∈ (
1
2
) for wh ich
0
1
0 but for which pla yer 1 loses
with probab ility 1. This implies that the expected payoff from this
bidisnegative,andplayer wouldbebetteroff bidding 0 instead.
Hence,
1
=
2
must hold. ()
1
6=
2
: Witho ut loss assum e that
1
2
. This means that there are values of
0
2
∈ (
1
2
) for whi ch
1
0
2
1 but for w hich player 2 wins with prob ability 1. But
then play er 2 could replace
0
2
with
00
2
=
0
2
− with small enough
such that
1
00
2
0
2
1, he will win with proba bility 1 and pay
less than he would pa y with
0
2
. Hence,
1
=
2
must hold. ¥
ii. Show that if two such strategies are a mixed strategy Nash equilib-
rium then it m ust be that
1
=
2
=0
Answ er: Assume not so that
1
=
2
= 0. This means that
when player bids
then he loses with probability 1, and get
an expected pa yoff of −
0. But instead o f biddin g pla y er
can bid 0 and receive 0 w hich is better than −
, imp lying that
1
=
2
= 0 cannot be an equilibrium. ¥
iii. Using the abo ve, argue that if t wo such strategies are a mixed strat-
egy Nash equilibrium then both pla yers m u st be getting an expected
pa y off of zero.
Answ er: As proposition 6.1 states, if a player is randomizing be-
t ween two alternatives then he m u st be indifferent betw een them.
Because both players are including 0 in the support of their mixed
strategy, their pa yoff from 0 is zero, and hence their expected pa yoff
from any ch oice in equilibrium m u st be zero. ¥
iv. Show that if two such strategies are a mixed strategy Nash equilib-
rium then it m ust be that
1
=
2
=1
Answ er: Assume not so that
1
=
2
= 1.From()abovethe
expected payoff from any bid in [0
] is equal to zero. If one of the

6. Mixed Strategies 109
play ers deviates from this strategy and choose to bid + 1 then
he will win with probab ility 1 and receiv e a payoff of 1−(
+) 0,
con tradicting that
1
=
2
= 1 is an equilibrium. ¥
v. Sho w that
() being uniform over [0 1] is a symm etric Nash equi-
librium of this game.
Answ er: Ima g ine tha t player 2 is playing accor ding to the pro-
posed strategy
2
() uniform ov er [0 1].Ifplayer1 bids some value
1
∈ [0 1] then his expected pa yoff is
Pr{
1
2
}(1−
1
)+Pr{
1
2
}(−
1
)=
1
(1−
1
)+(1−
1
)(−
1
)=0
imply ing that player 1 is willing to bid an y value in the [0 1] in terval,
and in particular, c hoosing a bid according to
1
() uniform o ver
[0 1]. Hence, this is a symm etric Nash equilibrium. ¥
11. Bribes: Two play ers find themselves in a legal battle over a paten t. The
patent is worth 20 foreachplayer,sothewinnerwouldreceive20 and the
loser 0.Giventhenormsofthecountrytheyarein,itiscommontobribe
the judge of a case. Each pla yer can offer a bribe secretly, and the one whose
bribe is the largest is awarded the patent. If both c hoose not to bribe, or
if the bribes are the same amount, then eac h has an equal c han ce of being
a warded the patent. If a pla yer does bribe, then bribes can be either a value
of 9 or of 20. Any other number is considered to be very unluc ky and the
judge w ould surely rule against a part y who offers a different n umber.
(a) Find the uniq ue pure-strategy N ash equilibr ium of this game.
Answ er: The gam e is captured in the follow ing two player matrix,
where represents no paym ent, represents a bribe of 9 and a
bribe of 20. For exam ple, if both choose 9 then they have an equal
110 6. Mixed Strategies
c hance of getting 20, so the expected payoff is
1
2
× 20 − 9=1,
Player 1
Player 2
10 10 0 11 0 0
11 0 1 1 −9 0
0 0 0 −9 −10 −10
It is easy to see th at is strictly dominated by .Intheremaining
game, is strictly dom in ate d by , and hence ( ) is the unique
Nash equilibrium . ¥
(b) If the norm were different so that a bribe of 15 w ere also acceptable, is
there a pure strategy Nash equilibrium?
Answ er: Now the game is as follo w s (where denotes a bribe of 15),
Player 1
Player 2
10 10 0 11 0 5 0 0
11 0 1 1 −9 5 −9 0
5 0 5 −9 −5 −5 −15 0
0 0 0 −9 0 −15 −10 −10
Using the best responses of eac h player it is easy to see that there is no
pure strategy Nash equilibrium . ¥
(c) Find the sym m etric mixed-strateg y Nash equilibrium for the game with
possible bribes of 9 15 and 20
Answ er: Note first that is w ea kly domina te d by ,soconsiderthe
game without ,
Play er 1
Player 2
10 10 0 11 0 5
11 0 1 1 −9 5
5 0 5 −9 −5 −5

6. Mixed Strategies 111
Let
=(
) denote a mixed strategy for p layer where
=1−
−
. The game is symmetric so for player 1 to be
indiffer ent bet ween and it must be that,
10
2
=11
2
+
2
− 9(1 −
2
−
2
)
which implies that
2
=
9
10
−
2
.Forplayer1 to be indifferent bet ween
and it must be that,
10
2
=5
2
+5
2
− 5(1 −
2
−
2
)
which im plies tha t
2
=
1
2
. Hence, the unique (mixed strategy) Nash
equilib riu m has each player play
=(
2
5
1
2
1
10
). ¥
12. The Tax Man: A citizen (play er 1) m ust c hoose whether or not to file taxes
honestly or whether to cheat. The tax man (pla y er 2) decides how m uc h effort
to in vest in auditing and can c hoose ∈ [0 1], and the cost to the tax man of
investing at a lev el is ()=100
2
. If the citizen is honest then he receives
the benc hmark pa yoff of 0, and the tax man pays the auditing costs without
an y benefit from the audit, yielding him a pa yoff of (−100
2
). If the citizen
c h eats then his pa yoff depends on whether he is caught. If he is caught then
his payoff is (−100) and the tax man’s payoff is 100 − 100
2
.Ifheisnot
caugh t then his payoff is 50 whilethetaxman’spayoff is (−100
2
) If the
citizen cheats and the tax man chooses to audit at lev el then the citizen is
caught with probability and is not cau ght with proba bility (1 − ).
(a) If the tax man believ es that the citizen is cheating for sure, w ha t is his
best response level of ?
Answ er: The tax man maximizes (100 −100
2
)+(1−)(0−100
2
)=
100 − 100
2
.Thefirst-order optimality condition is 100 − 200 =0,
yielding =
1
2
. ¥
(b) If the tax man believes that the citizen is ho nest for sure, what is h is
best response level of ?
112 6. Mixed Strategies
Answ er: The tax man maximizes −100
2
which is maxim ized at =0.
¥
(c) If the tax man believes that the citizen is honest with probab ility ,
what is his best response level of as a function of ?
Answ er: The tax man maximizes (−100
2
)+(1−)(100 −100
2
)=
100(1 −) −100
2
.Thefirst-ord er optimality condition is 100(1 −)−
200 =0, yielding the best response functio n
∗
()=
1−
2
. ¥
(d) Is there a pu re strategy Nash equilibrium o f th is game? W hy or why
not?
Answ er: T here is no pure strategy N ash equilibrium. To see this, con-
sider the best response of player 1 who believ e s that pla yer 2 c hooses
some lev el ∈ [0 1].Hispayoff from being honest is 0 wh ile his payoff
from c h ea ting is (−100) + (1 −)50 = 50 − 150. Hence, he prefers to
be honest if and only if 0 ≥ 50 − 150 or ≥
1
3
. Letting
∗
() denote
the best response correspondence of player 1 as the probability that he
is honest, we hav e that
∗
()=
⎧
⎪
⎨
⎪
⎩
1 if
1
3
[0 1] if =
1
3
0 if
1
3
and it is easy to see that there are no values of and for wh ich both
pla yers are play ing mutual best responses. ¥
(e) Is there a mixe d strate gy Nash equilibrium of this gam e? Why or wh y
not?
Answ er: From (d) above w e kno w that pla yer 1 is willing to mix if
and only if =
1
3
, which must therefore hold true in a mixed strategy
Nash equilibrium. For play er 2 to be willing to pla y =
1
3
we use his
best response from part (c),
1
3
=
1−
2
, which yields, =
1
3
. Hence, the
uniqu e mixed strategy Nash equilibriu m has player 1 being honest with
probab ility
1
3
and pla yer 2 c hoosing =
1
3
. ¥
Part III
Dynamic Games of Complete
Information
113
114
This is page 115
Printer: Opaque
t
7
P r elimina r ies
1. Strategies: Im a gin e an extensive form game in which pla yer has infor-
matio n sets.
(a) If the player has an identical nu mber of possible action s in each
informationset,howmanypurestrategiesdoeshehave?
Answ er: The play er has
pure strategies.
(b) If the play er has
actions in information set ∈ {1 2 },how
many pure strategies does the player ha ve?
Answ er: The play er has
1
×
2
×···×
pure strategies. ¥
2. Strate gies and equilibrium : Consider a two player game in wh ich player
1canchoose or . The game ends if he chooses w h ile it continu es to
player 2 if he chooses .Player2canthenchoose or ,withhegame
ending after and con tinuing again with player 1 after . Player 1 then can
choose or , and the game ends after each of these choices.
(a) Model this as an extensive form game t ree. Is it a game of perfect or
imperfect informa tio n?

116 7. Preliminaries
Answ er:
This gam e is a game of perfect informatio n . ¥
(b) Ho w man y terminal nodes does the game ha v e? Ho w man y information
sets?
Answ er: The game has 4 terminal nodes (after choices A, C, E and F)
and 3 information sets (one for each player. ¥
(c) Ho w ma ny pure strategies does each pla yer ha ve?
Answ er: Player 1 has 4 pure strategies and player 2 has 2. ¥
(d) Imagine that the pa yoffsfollowingchoice by player 1 are (2 0),fol-
lowing by player 2 are (3 1), follo w ing by player 1 are (0 0) and
follow in g by player 1 are (1 2). Wha t are the Nash equilibria of this
game? Does one strik e y ou as more “appealing” than the other? If so,
explain why.
Answ er: We can write down the matrix form of this game as follows
( denotes a strategy for player 1 where ∈ { } is what he does
in his firstinformationsetand ∈ {} in his second one),
Play er 1
Player 2
2 0 2 0
2 0 2 0
3 1 0 0
3 1 1 2
7. Preliminaries 117
It’s easy to see that there are three pure strategy Nash equilibria:
( ) ( ) and ( ). The equilibria ( ) ( ) are
Pareto dom inated by the equilibrium ( ), and hence it would be
temp ting to argue that ( ) is the mo re “appealing” equilibrium .
AswewillseeinChapter8itisactually( ) that has properties
that are more appealing (sequential rationality). ¥
3. Tick-tack-toe: The extensiv e form represen tation of a game can be cumber-
some even for very simple games. Consider the game of Tick-tack-toe where
2 pla yers mark “”or“”ina3 × 3 matrix. Play er 1 mov es first, then
play er 2, and so on. If a player gets three of his kind in a row , column, or
one of the diagon als then he wins , and otherwise it is a tie. For this question
assum e that even after a winner is declared, the players mu st co mple t e ly fill
the matrix before the game ends.
(a) Is this a game of perfect or imperfect information? Why?
Answ er: This is a game of perfect information because each pla yer
knows exactly what transpired before he m oves, and hence every infor-
mation set con tains one node. ¥
(b) Ho w many inform a tion sets d oes pla yer 2 have after player 1’s first
move?
Answ er: Pla yer 2 has 9 inform ation sets, one for eac h of the moves of
player 1. ¥
(c) How many information sets does player 1 have after each of pla yer 2’s
first move?
Answ er: Play er 2 has 8 possible mo ves in his first turn, and this is
true for each one of the 9 possible moves that pla yer 1 has in hid first
turn. Hence, player 1 has 9×8=72inform ation sets in his second move
(after pla yer 2’s first mo ve).
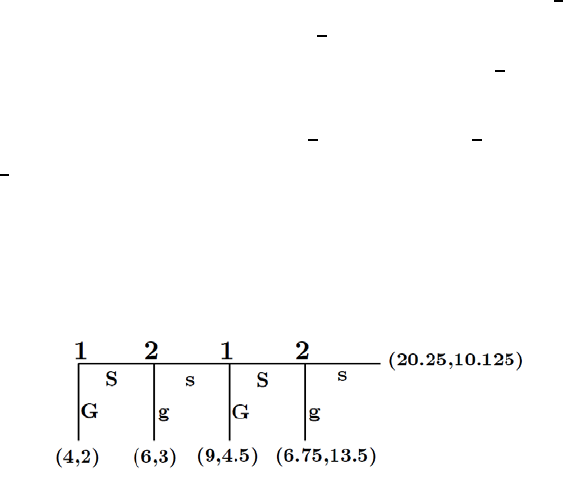
118 7. Preliminaries
(d) Ho w many information sets does each pla yer ha ve in total? (Hin t: For
this and the next part y ou may want to use a program like Excel.)
Answ er: Continuing the logic of part (c), after player 1’s second mo ve,
player 2 has 9 × 8 × 7=504information sets, then pla yer 1 has 9 × 8 ×
7 × 6=3 024 informationsets,andsoon(15 120; 60 480; 181 440 and
362 880). We add the alternating n umbers to get ho w many information
set each player has, and we ha ve to remember to add the root which
belongs to player 1. Hence, pla yer 1 has 426,457 information sets while
player 2 has 197,073. ¥
(e) Ho w many terminal nodes does the game have?
Answ er: The number of terminal nodes is equal to the number of
information sets in pla yer 1’s last turn because at that pint he just has
one mo v e, to complete the tick-tack-toe matrix, whic h is 362 880. ¥
4. Cen tipedes: Imagine a two pla y er game that proceeds as follows. A pot of
money is created with $6 in it initially. Play e r 1 moves first, then pla yer 2,
then pla yer 1 again and finally pla yer 2 again. At eac h player’s turn to mo ve,
he has two possible actions: grab ()orshare(). If he grabs, he gets
2
3
of
thecurrentpotofmoney,theotherplayergets
1
3
of the pot and the game
ends. If he shares then the size of the current pot is multiplied b y
3
2
and the
next player gets to mov e . At th e last stage in which player 2 mo ves, if he
chooses share then the pot is still mu ltiplied by
3
2
,player2gets
1
3
of the pot
and player 1 gets
2
3
of the pot.
(a) Model this as an extensive form game t ree. Is it a game of perfect or
imperfect informa tio n?
Answ er:
7. Preliminaries 119
This is a game of perfect informat ion . Note that we draw the game from
left to right (which is the common con vention for “cen tipede games” of
this sort.) We use capital letters for player 1 and lo wer case for pla yer
2. ¥
(b) Ho w man y terminal nodes does the game ha v e? Ho w man y information
sets?
Answ er: Thegamehasfive terminal nodes and four information sets.
¥
(c) Ho w ma ny pure strategies does each pla yer ha ve?
Answ er: Each play er has four pure strategies (2 actions in eac h of his
2 information sets). ¥
(d) Find the Nash equilibr ia of this gam e. How many outcom es can be
supported in equilibrium?
Answ er: Using the convention of to denote a strategy of player
where he c h ooses in his first information set and in his second, we
can dra w the following matrix representation of this game,
Player 1
Play er 2
4 2 4 2 4 2 4 2
4 2 4 2 4 2 4 2
3 6 3 6 9 45 9 45
3 6 3 6 675 135 2025 10125
We see that only one outcome can be supported as a Nash equilibrium:
player 1 grabs imm ediately and the players’ payoffsare(4 2). ¥
(e) Now imag ine that at the last stage in whic h play er 2 moves, if he chooses
tosharethenthepotisequallysplitamongtheplayers.Doesyour
answer to part (d) above chan ge?
Answ er: The answ er does change because the pay offs from the pair of
120 7. Preliminaries
strategies ( ) c hanges from (2025 10125) to (151875 151875) in
which case pla yer 2’s best response to will be , and player 1’s best
response to remains ,sothat() is another Nash equilibrium
in which they split 30375 equally (the previous Nash equilibria are still
equilib ria ). ¥
5. Veto Power: T wo pla yers must choose between three alternatives, and
. Pla yer 1’s preferen ces are given by Â
1
Â
1
while player 2’s preferences
are giv en by Â
2
Â
2
. The rules are that player 1 moves first and can
veto one of the three alternativ e s. Then, play e r two chooses whic h of th e
rema in ing two alternatives will be chose n.
(a) Model this as an extensiv e form game tree (choose pay o ffsthatrepre-
sen t the preferences).
Answ er: Assume that the pay off of the best option is 3, the second best
2 and the w orst is 1. Player1’s actions are which alternativ e to remo ve
and player 2’s whic h of the remain ing two to choose.
¥
(b) Ho w ma ny pure strategies does each pla yer ha ve?
Answ er: Player 1 has three pure strategies while play er 2 has eigh t (2
actions in each of three information sets.) ¥
(c) Find all the Nash equ ilibr ia of this game.

7. Preliminaries 121
Answ er: Let be a strategy for pla y er 2 where is w h at he does
follow ing the remo val of , fo r and for so that we can use the
follow ing m a t r ix,
Player 1
Player 2
2 2 2 2 2 2 2 2 1 3 1 3 1 3 1 3
3 1 3 1 1 3 1 3 3 1 3 1 1 3 1 3
3 1 2 2 3 1 2 2 3 1 2 2 3 1 2 2
and we see that is the only outcome that an be supported as an
equilib rium via two Nash equilibria , ( ) and ( ) ¥
6. Entering an Industry: A firm (pla yer 1) is considering entering an estab-
lished industry with one incumbent firm (player 2). Player 1 must c hoose
whether to enter or to not enter the industry. If play er 1 enters the industry
then play er 2 can either accomm odate the entry, or fight the entry with a
price w a r. Pla yer 1’s most pr eferred outcom e is entering with pla yer 2 not
fighting, and his least preferred outcome is entering with pla yer 2 fighting.
Player 2’s most preferred outcome is pla yer 1 not entering, and his least
preferred outcome is player 1 enter ing with play er 2 fighting.
(a) Model this as an extensiv e form game tree (choose pay o ffsthatrepre-
sen t the preferences).
Answ er:
122 7. Preliminaries
(b) Ho w ma ny pure strategies does each pla yer ha ve?
Answ er: Each player has two pure strategies. ¥
(c) Find all the Nash equ ilibr ia of this game.
Answ er: Th ere are two Nash equilibria which can be seen in the matrix,
Play er 1
Player 2
0 2 0 2
1 1 −1 −1
Both ( ) and ( ) are Nash equilibria of this game. ¥
7. Roommates Voting: Three roommates need to vote on whether they will
adopt a new rule and clean their room once a week, or stick to the current
once a mon th rule. Each votes “y es” for the new rule or “no” for the curren t
rule. Imagine that players 1 and 2 prefer the new rule while player 3 prefers
the old rule.
(a) Imagine that the pla yers require a unanimou s vote to adopt the new
rule. Player 1 vot es first, then player 2, and then player 3, e ach one
observing the previous v otes. Dra w this as an extensive form game and
find the Nash equ ilibr ia.
Answ er: The game is,
7. Preliminaries 123
and there are man y Nash equilibria. Player 1 has two pure strategies:
and .Player2has4:{} (where the left entry corre-
sponds to his left information set) and player 3 has 16 (again, with the
natural left to righ t in terpretation): {
}.Because
a unanimous v ote is needed, the only strategy profiles t hat are not a
Nash equilibrium are those for whic h players 1 or 2 can ch ang e a “no”
v o te to a “ye s” vote, or player 3 can chan ge a “yes” v ote to a “no”
vote. These profiles are () ( ) where ∈ {}
from whic h player 1 can profitably deviate from ;()( )
from which player 2 can pr o fitably devia te fro m to ;and()
( ) from which player 3 can profitably deviate from
to . Th u s, the Nash equilibria are profiles of strategies that belong
to one of two classes: () player 3 votes and players 1 and 2 vote
anything (a total of 64 strategy profiles which include 8 of player 3, 4
of play er 2 and 2 of play er 1); ()player3 votes , player 2 votes
and player 1 votes (a total of 16 strategy profiles whic h include 8
of player 3, 2 of player 2 and 1 of player 1). All the outcomes ha ve the
curren t rule surviving. ¥
(b) Imagine now that the pla yers require a majority vote to adopt the new
rule (at least two “y es” votes). Again, player 1 votes first, then pla yer
2, and then pla yer 3, each one observing the previous v otes. Dra w this
as an extensive form gam e and find the Nash equilibria.
Answ er: The game’s pa y off no w c hange as follows,
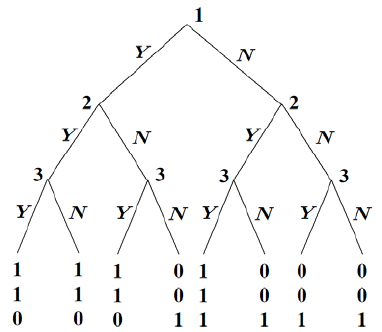
124 7. Preliminaries
Now only a majorit y vote is needed, but still, the only strategy profiles
that are not a Nash equilibrium are those for which players 1 or 2 can
c hange a “no” v ote to a “yes” vote, or pla yer 3 can c hange a “yes” v o te
to a “no” vote. Th ese profiles are () ( ) or ( )
where ∈ {} fromwhichplayer1canprofitably devi-
ate from ;()() or ( ) from wh ich player 2
can profitab ly deviate from to or from to ;and()
( )or( ) from whic h pla yer 3 can profitably de-
viate from to or from to .Thus,theNash
equilib ria are profiles of strategies that belong to one of two classes: ()
player 3 votes , player 1 votes and 2 v otes (a total of 32
strategy profiles whic h include 16 of play er 3, 2 of pla yer 2 and 1 of
pla yer 1). These all ha ve players 1 and 2 v o ting and support the new
rule; ()player3 votes ,player2votes and pla yer 1 votes
(a total of 8 strategy profi
les whic h include 4 of play er 3, 2 of pla yer 2
and 1 of pla yer 1). These have pla yers 1 and 3 or 1 and 2 (or all three)
vote and support the curren t rule surviving, and neither player 1 nor
2 can change the outcome by deviating unilaterally. ¥
(c) Now imagine that the gam e is lik e in part (b), but the pla yers put their
v o tes in a hat, so that the votes of earlier mo vers are not observed by
the votes of later mo vers, and at the end the v otes are counted. Draw
this a s an extensive form gam e and find the Nash equilib ria. In w ha t
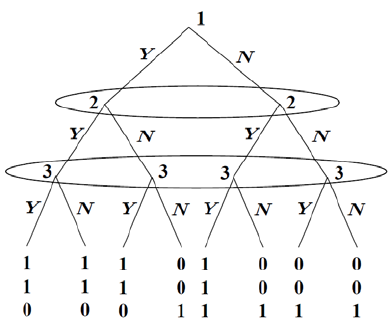
7. Preliminaries 125
wayisthisdifferent from the result in (b) above?
Answ er: This gam e is on e of imperfect info rm ation where eac h player
has one information set,
Lik e part (b), an y strategy in whic h both players 1 and 2 are v ot-
ing oroneinwhichthereareatleast2novotesthatcannotbe
c h ang ed to only one by pla yers 1 and 2 will be an equilibrium, but
the strategy sets are small because pla yers 2 and 3 cannot condition
their play on the history of what the “previous” players did . Hence,
for each pla yer the strategy set is
= { } and the Nash equilib ria
are (
1
2
3
) ∈ {( ) ( ) ( )}.Likeinpart(b)both
outcom es can be supported by a N ash equilibrium, just th at no w the
strategy combination s that support it are fewer. ¥
8. Brothers: Consider the followin g game that proceeds in t wo steps: In the
first stage one brother (pla yer 2) has t wo $10 bills and can c hoose one of t wo
options: he can give his you nger brother (player 1) $20, or give him one of
the $10 bills (giving nothing is inconceivable giv en the wa y they were raised.)
This money will be used to buy snack s at the show they will see, and each
one dollar of snack yields one unit of pa yoff for a player who uses it. The
126 7. Preliminaries
show they will see is determin ed by the follow ing “battle of the sexes” gam e:
Player 1
Player 2
16,12 0,0
0,0 12,16
(a) Presen t the entire gam e in extensive form (a game tree).
Answ er: Let the choices of play er 1 first be fo r spliting the $2 0 and
for giving it all away. T he en tire game will hav e the payoffsfromthe
c hoice of ho w to split the money added to the pa y offs from the Battle
of the Sexes part of the game as follows,
Because the latter is simultaneous, it does not mater which pla y er mo ves
after pla yer 1 as long as the last pla yer cannot distingu ish between the
choiceoftheplayerwhomovesjustbeforehim.¥
(b) Write the (pure) strategy sets for both pla yers.
Answ er: Both players can conditio n their choice in the Battle of the
Sexes gam e on th e initial split/give c ho ice of player 1. For player 2,
2
= {} where
2
= means that player 2 chooses
∈ { } afterplayer1chose while pla yer 2 chooses ∈ { }
after player 1 ch ose . For player 1, however, even though he chooses
first bet ween or , he must specify his action for eac h information
set even if he knows it will not happen (e.g., wha t he will do follo w in g
7. Preliminaries 127
even w hen he plans to play ). Hence, he has 8 pure strategies,
1
= { } where
1
=
means that pla y er 1 first c hooses ∈ { } andthenchooses
∈ { } if he pla yed and ∈ { } if he played . ¥
(c) Presen t the entire gam e in one matrix.
Answ er: This will be a 8 × 4 matrix as follows,
Play er 1
Player 2
26 22 26 22 10 10 10 10
26 22 26 22 10 10 10 10
10 10 10 10 22 26 22 26
10 10 10 10 22 26 22 26
16 32 0 20 16 32 0 20
0 20 12 36 0 20 12 36
16 32 0 20 16 32 0 20
0 20 12 36 0 20 12 36
(d) Find the Nash equilibria of the entir e game (pure and mixed strategies).
Answ er: First note that for play er 1, mixing equally bet ween and
will strictly dominate the four strategies and
. Hence, we can consider the reduced 4 × 4 game,
Play er 1
Player 2
26 22 26 22 10 10 10 10
26 22 26 22 10 10 10 10
10 10 10 10 22 26 22 26
10 10 10 10 22 26 22 26
The simple ov erline-underline method shows that w e ha ve eigh t pure
strategy Nash equilibria, four yielding the pay offs (26 22) and the other
128 7. Preliminaries
four yielding (22 26). Because of each players indifference between the
w a ys in which the pa y offs are reac hed, there are infinitely man y mixed
strategies that y ield the same payoffs. For exam ple, an y profile where
pla yer 1 mixes bet ween and and where player 2 mixes be-
tween and w ill be a Nash equilibrium that yields (26 22).Sim-
ilarly, any profile wher e play er 1 mixes bet ween and and
where player 2 mixes between and will be a Nash equilibrium
that yields (22 26). There is, however, one more class of m ixed strategy
Nash equilibria that are similar to the one found in section 6.2.3. To see
this, focus on an e ven simpler game where we eliminate the duplicate
pa y offsasfollows,
Play er 1
Player 2
26 22 10 10
10 10 22 26
which p reserve th e nature of the gam e. For player 1 to be indifferent
between and it must be that player 2 chooses with
probab ility such that
26 +10(1− )=10 +22(1− )
which yields =
3
7
. Similarly, for player 2 to be indifferen t between
and it m u st be that player 1 chooses with probability such
that
22 + 10(1 − )=10 +26(1− )
which yields =
4
7
. Hence, we found a mixed strategy Nash equilibrium
that results in each player getting an expected pa yoff of 26×
3
7
+10×
4
7
=
16
6
7
Notice, however, tha t player 1 is always indifferen t bet ween
and ,aswellasbetween and so there are infinitely
many w ays to ac hieve this kind of mixed strateg y, and similarly for
player 2 because of his indifference between and as w ell as
and . ¥
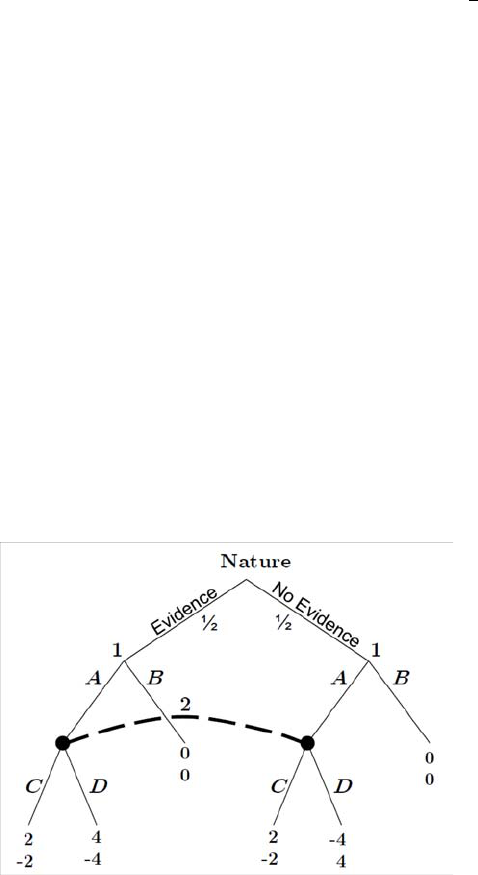
7. Preliminaries 129
9. The Dean’s Dilemm a: A student stole the DVD from the studen t lounge.
The dean of studen ts (player 1) suspects the student (player 2) and engages
in evidence collection. Ho wever, evidence collection is a random process, and
concret e evidence will be available to the dean only with probability
1
2
.The
student knows the evidence generating process, but does not kno w whether
the dean received eviden ce or not. The game proceeds as follow s: The dean
realizes if he has evidence or not, and then can choose his action, whether to
Accuse the studen t (), or Bounce the case () and forget it. Once accused,
the studen t has two options: he can either Confess ()orDeny().
Payoffs are realized as follow s: If the dean bounces the case then both play ers
get 0. If the dean accuses the student, and the student confesses, the dean
gains 2 and the studen t loses 2. If the dean accuses the student and the
student denies, then pa y offs depend on the evidence: If the dean has no
evidence then he loses face which is losing 4, while the studen t gains glory
which gives him a payoff 4. If, ho wev er, the dean has evidence then he is
triumphant and gains 4, while the studen t is put on probation and loses 4.
(a) Dra w the game-tree that represents the extensiv e form of this game.
Answ er: Letting the Dean be pla yer 1 and the studen t play er 2,
¥
(b) Write down the matrix that represen ts the normal form of the extensive
form you did in (a) abo ve.
130 7. Preliminaries
Answ er: Because player 1 can condition whether or not to accuse
on whether or not there is evidence, he has four pure strategies. Let
∈ { } be the strategy of player 1 wh ere follow s
“evidence” and follow s “no evidence.” Player 2 does not kno w whether
there is evidence and can only respond by confessing or not:
Play er 1
Player 2
2 −2 0 0
1 −1 2 −2
1 −1 −2 2
0 0 0 0
¥
(c) Solv e for the Nash Equilibria of the game.
Answ er: It is easy to see that is strictly domina ted b y and
is strictly domin ated b y . The reduced gam e is therefore,
Play er 1
Player 2
2 −2 0 0
1 −1 2 −2
Let play er 1 c hoose with probability and player 2 c hoose with
probab ility . For pla yer 2 to be indifferentitmustbethat
(−2) + (1 − )(−1) = (0) + (1 − )(−2)
and the solution is =
1
3
. Similarly, for player 1 to be indifferentitmust
be that
(2) + (1 − )(0) = (1) + (1 − )(2)
and the solution is =
2
3
. Hence, ( )=(
1
3
2
3
) istheuniquemixed
strategy Nash equilibrium of this game. As you will see in c hap ter 15,
this is a dyna m ic gam e of incomplet e information. ¥
7. Preliminaries 131
10. P erfect and Imperfect Recall: Consider the game dep icted in Figure ??
Exercise
(a) What are the pure strategies sets for eac h play er?
Answ er: T
(b) Show that for an y behavioral strategy for player 1, there is a mixed
strategy that leads to the same distribution ov er the terminal nodes
regardless of the strategy c hosen by pla yer 2.
Answ er: T
(c) Show that for an y behavioral strategy for player 2, there is a mixed
strategy that leads to the same distribution ov er the terminal nodes
regardless of the strategy c hosen by pla yer 1.
Answ er: T
(d) No w imagin e that the game does not have perfect recall so that player
2’s two bottom information sets are no w one large information set. Can
you find an example sho wing that the claim in (a) abo v e is no longer
true?
Answ er: T
132 7. Preliminaries
This is page 133
Printer: Opaque
t
8
C r e d ib ility a n d Se q u e ntia l R a t ionality
1. Find the mixed strategy subgame perfect equilibrium of the Sequen tial Battle
of the Sexes game depicted in Figure ??
Answ er: The subg ame starting with play e r 1 c h oosing bet ween and is
given in the follo w ing ma trix:
Player 1
Player 2
2 1 0 0
0 0 1 2
Let player 1 choose with probab ility and pla yer 2 c hoose with proba-
bility .Forplayer2tobeindifferent it must be that
(1) + (1 − )(0) = (0) + (1 − )(2)
and the solution is =
2
3
. Similarly, for pla yer 1 to be ind ifferentitmustbe
that
(2) + (1 − )(0) = (0) + (1 − )(1)
and the solution is =
1
3
. Hen ce, ( )=(
1
3
2
3
) is the unique mixed strategy
Nash equilibrium of this subgame with expected payoffsof(
1
2
)=(
2
3
2
3
).
Working backward, pla yer 1 w ould prefer to c hoose over . ¥
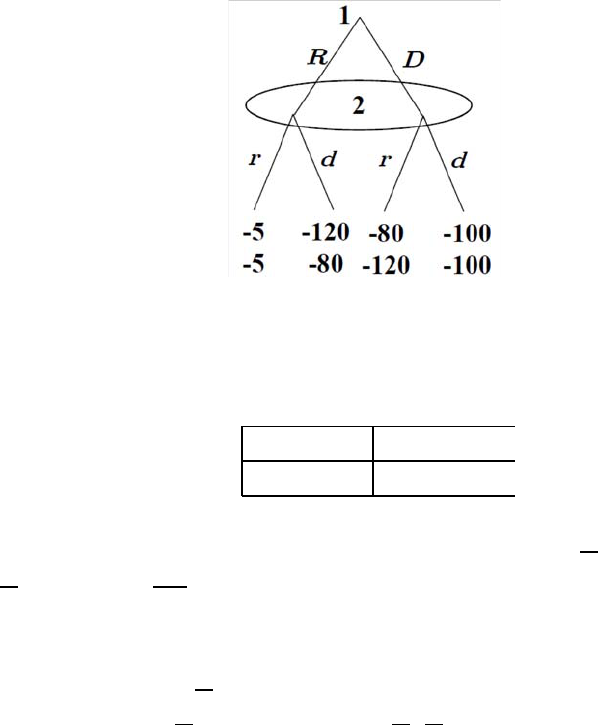
134 8. Credibility and Sequential Rationality
2. M utu ally Assure d De struction (revisite d): Consider the game in sec-
tion ??.
(a) Find the mixed strategy equilibrium of the w ar stage game and argue
that it is unique.
Answ er: The war-game in the text has a weakly dominated Nash equi-
librium ( ) and hence does not ha ve an equilibrium in which any
player is mixing. This exercise should have replaced the war-stage game
with the follow ing gam e:
The subgame we called the w ar -stag e gam e is given in the follow ing ma-
trix:
Play er 1
Play er 2
−5 −5 −120 −80
−80 −120 −100 −100
Let player 1 c hoose with probabilit y and player 2 choose with
probab ility .Forplayer2tobeindifferentitmustbethat
4
19
(−5) +
(1 −
4
19
)(−120) = −
1820
19
(−5) + (1 − )(−120) = (−80) + (1 − )(−100)
and the solution is =
4
19
.Bysymmetry,forplayer1tobeindifferen t
it must be that =
4
19
. Hence, ( )=(
4
19
4
19
) is the unique mixed
strategy Nash equilibrium of this subgame with expected pa yoffsof
(
1
2
)=(−9578 −9579). ¥

8. Credibility and Sequential Rationality 135
(b) What is the unique subgame perfect equilibrium that includes the mixed
strategy you found abo ve?
Answ er: Working backward, play er 2 w ould prefer to ch oose over
andplayer1wouldprefer over .
3. Bro the rs (revisited ): Find all the subgame prefect equilibria in the “broth-
ers” exercise (exercise 7.8) from the previous c h apter .
Answ er: In part (d) o f exercise 7.8 w e found all the N ash equilibria as
follo w s: For pla yer 2,
2
= {} where
2
= means that
play er 2 chooses ∈ { } after play er 1 chose while player 2 c h ooses
∈ { } after pla yer 1 chose .Forplayer1,
1
= { } where
1
=
meansthatplayer1first c h ooses ∈ { } and then chooses ∈ { } if
he played and ∈ { } if he played .Wefirst noted that for player
1, mixing equa lly bet ween and will strictly dominate the four
strategies and . Hence, w e can consider the reduced
4 × 4 game,
Player 1
Play er 2
26 22 26 22 10 10 10 10
26 22 26 22 10 10 10 10
10 10 10 10 22 26 22 26
10 10 10 10 22 26 22 26
Thesimpleoverline-underlinemethodshowsthatwehaveeightpurestrategy
Nash equilibria, four yielding the payoffs (26 22) and the other four yielding
(22 26).
Now w e know that any subgam e perfect equ ilibrium must be a N ash equi-
librium , so w e can consider the set of Nash equilibria and see which surviv es
backward induction. Because the second stage of the game has play ers 1 and
2 move simu ltaneo usly, the only restriction of subgam e perfection is that in
eac h of the simultaneous move games, the players are playing a Nash equi-
librium. This implies that the pairs of strategies () and ()
136 8. Credibility and Sequential Rationality
are not subgame perfect, which is also true for () and ().
Hence , of the eigh t pure strategy Na sh equilibria only four are subgame per-
fect: ( ),(),() and ().
Because of each players indifference bet ween the w ays in w h ich the p ayoffs
are reached, there are infinitely many mixed strategies that yield the same
pa y offs. For example, any profile where pla yer 1 mixes between and
and wher e player 2 m ixes bet ween and w ill be a N ash equilib-
rium that yields (26 22). Sim ilarly, any profile wh ere player 1 mi xes between
and and where play er 2 mixes between and will be a
Nas h equilibriu m that yields (22 26). But most of these will not be subgame
perfect because in the subgame following ,whichisoff the equilibrium path,
the pla yers are not playing a best response. There is, however, one more class
of mixed strategy Nash equilibria that are similar to the one found in section
6.2.3. To see this, focus on an ev e n simpler game where we eliminate the
duplicate pay offsasfollows,
Play er 1
Play er 2
26 22 10 10
10 10 22 26
which preserv e the nature of the game. For player 1 to be indifferent between
and it must be that pla yer 2 chooses with probability such
that
26 +10(1− )=10 +22(1− )
wh ich yie lds =
3
7
. Similarly, for player 2 to be indifferent between and
it must be that player 1 ch ooses with prob ability suc h that
22 +10(1− )=10 + 26(1 − )
which yields =
4
7
. Hence, we found a mixed strategy Nash equilibrium that
results in eac h pla yer getting an expected pa yoff of 26 ×
3
7
+10×
4
7
=16
6
7
Notice, ho wev er, that player 1 is always indifferent between and ,
as w ell as between and so there are infinitely man y wa ys to
8. Credibility and Sequential Rationality 137
ac h ieve this kind of mixed strategy, and similarly for player 2 because of
his indifference between and as well as and .Themixed
strategy subgame perfect equilibria will be those for which in each subgame
the players are play ing a Na sh equilibr ium , and hence there will be only 6
such pairs: wh ere they mix after and pla y one of three Nash equ ilibria in
the subgam e after , and similarly where they mix after and play one of
the three Nash equilibria in the subga m e after . In all of these player 1’s
backward induction choice is the play . ¥
4. The Industry Leader: Three oligopolists operate in a mark et with in v erse
demand giv en by ()=− ,where =
1
+
2
+
3
,and
is the quantity
produced b y firm .Eachfirm has a constan t marginal cost of production, ,
and no fixed cost. The firm s c h oose their quantities dynamically as follow s:
(1) Firm 1, wh o is the industry leader, chooses
1
≥ 0 ; (2) Firms 2 and 3
observ e
1
and then sim ultaneously c hoose
2
and
3
respectively.
(a) Ho w m an y proper subgames does this dynamic game ha ve? Explain
Briefly.
Answ er: There are infinitely many proper subgame s because ev ery
quantit y choice of pa yer 1 results in a proper subgam e. ¥
(b) Is it a game of perfect or imperfect informa tion ? Explain Briefly.
Answ er: Th is is a game of imperfe ct inform ation because play e rs 2 and
3 make their choice without observing eac h other’s cho ice first. ¥
(c) What is the subgam e perfect equilibrium of this game? Show that it is
unique.
Answ er: first w e solve for the Nash equilib rium o f the simultan eous
move stage in which pla yers 2 an d 3 make their choices as a function
of the choice made first b y player 1 . Given a c h oice of
1
and a belief
about
3
player 2 maxim ize s
max
2
( − (
1
+
2
+
3
) − )
2
138 8. Credibility and Sequential Rationality
which leads to the first order condition
−
1
−
3
− − 2
2
=0
yielding the best response function
2
=
−
1
−
3
−
2
and symm etrically, the best response function of pla yer 3 is
3
=
−
1
−
2
−
2
.
Hence, follo wing an y choice of
1
b y pla yer 1, the unique Nash equilib-
rium in the resulting subga m e is the solution to the two best response
function s, which yields
∗
2
(
1
)=
∗
3
(
1
)=
− −
1
3
Moving bac k to pla yer 1’s decision node, he will ch oose
1
kno wing that
2
and
3
be be cho sen using the best response fu nction above, a nd
hence play er 1 maximizes,
max
1
( − (
1
+
− −
1
3
+
− −
1
3
) − )
1
which leads to the first order equation
1
3
( − − 2
1
)=0
resulting in a un ique solution
1
=
−
2
. H en ce, the unique subgame
perfect equilibriu m dictates that
∗
1
=
−
2
,and
∗
2
(
1
)=
∗
3
(
1
)=
−−
1
3
.
¥
(d) Find a Na sh equilibrium that is not a sub ga m e perfect equilibriu m .
Answ er: There are infinitely man y Nash equilibria of the form “if pla yer
1plays
0
1
then players 2 and 3 play
∗
2
(
0
1
)=
∗
3
(
0
1
)=
−−
0
1
3
, and oth-
erwise they play
2
=
3
= .” In any such Nash equilibrium, players
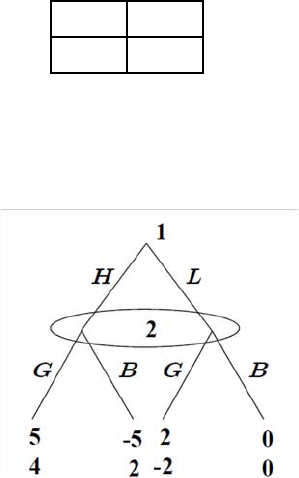
8. Credibility and Sequential Rationality 139
2 and 3 are playing a Nash e quilibriu m on the equ ilib riu m path (fol-
lowing
0
1
) w hile they are flooding the market and casing the price to
be zero off the equilibriu m path. One exam ple wo uld be
0
1
=0.Inthis
case, following
0
1
=0the remaining two play ers pla y the duopoly Nash
equilib riu m , and player 1 gets zero profits. If pla yer 1 were to choose
any positive quantity, his belief is that players 2 and 3 w ill flood the
market and he will earn −
1
0, so he w ould prefer to c h oose
0
1
=0
given those beliefs. Of course, the threats of pla yers 2 and 3 are not
sequentia lly rational, which is the reason tha t this Nash equilibr iu m is
not a subgame perfect equilibrium. ¥
5. Technology Adoption: During the adoption of a new technology a CE O
(player 1) can design a new task for a division manager. The new task can
either be a high level ()orlowlevel(). The manager simultaneously
chooses to invest in good training ()orbadtraining(). The payoffsfrom
this in teractio n is giv en by the following m atr ix:
pla yer 1
Play er 2
5 4 −5 2
2 −2 0 0
(a) Presen t the gam e in extensive form (a gam e tree) and solve for all the
Nash Equilibria and sub game perfect equilib ria .
Answ er:
140 8. Credibility and Sequential Rationality
It is easy to see in the m atrix above that both ( ) and ( ) are
pure strategy Nash equilibria. To find the mixed strategy Nash equilib-
rium, let player 1 choose with probability and pla yer 2 choose
with probability .Forplayer2tobeindifferentitmustbethat
(4) + (1 − )(−2) = (2) + (1 − )(0)
and the solution is =
1
2
. Similarly, for player 1 to be indifferentitmust
be that
(5) + (1 − )(−5) = (2) + (1 − )(0)
and the solution is =
5
8
. Hence, ( )=(
1
2
5
8
) istheuniquemixed
strategy Nash equilibrium of this game with expected payoffsof(
1
2
)=
(
5
4
1). ¥
(b) No w assume that before th e game is played the CEO can choose not
to adopt this new tec h nolo gy, in which case the pa yoffsare(1 1),orto
adoptitandthenthegameaboveisplayed.Presenttheentir e game in
extensiveform.Howmanypropersubgamesdoesithave?
Answ er:
The gam e has two proposer subgames. The firstisthewholegameand
the second starts at player 1’s secon d inform a tion set. ¥
(c) Solv e for all the Nash Equilibria and subgam e perfect equilibria of the
game described in (b) abo ve.

8. Credibility and Sequential Rationality 141
Answ er: The game can be represen ted by the following ma trix,
Play er 1
Play er 2
5 4 −5 2
2 −2 0 0
1 1 1 1
1 1 1 1
and it is easy to see that there are three pure strategy Nash equilib-
ria: ( ) () and (). From part (a) above w e know that
player 1 choosing followed by the mix ed strategy Nash eq uilib riu m
( )=(
1
2
5
8
) will be a (subgam e perfect) Nas h e quilibr ium with ex-
pected payoffsof(
1
2
)=(
5
4
1). Also, there are infinitely man y mixed
strategy Nash equilibria in which pla yer 1 is mixing bet ween and
in any arbitrary way and pla yer 2 c hooses .Finally,thereisan-
other infinite set of mixed strategy equilibria in which player 1 mixes
between , and , and pla yer 2 mixes bet ween and .Tosee
this, ignore for the moment (as it yields the same pa yoffsas),
and let play er 1 ch oose with probabilit y and with probability
(1 −), and let player 2 c h oose with probability .Forplayer2tobe
indifferentitmustbethat
(4) + (1 − )(−2) = (1) + (1 − )(1)
and the solution is =
1
2
. Similarly, for player 1 to be indifferentitmust
be that
(5) + (1 − )(−5) = (1) + (1 − )(1)
and the solution is =
3
5
. Hence, ( )=(
1
2
3
5
) is a mixed strateg y
Nash equilibrium of this game with expected payoffsof(
1
2
)=(1 1).
Of course, because of the iden tity bet ween the and any pair of
the following strategies will also be a mixed strategy Nash equilibriu m :
player 1 c hooses with p rob ability
1
2
,chooses and with
probab ilities that a dd up to the remaining
1
2
, and pla y er 2 chooses

142 8. Credibility and Sequential Rationality
with probability
3
5
.
Turning to subgame perfect equilibria, of the three Nash equilibria only
t wo are subgame perfect: ( ) and (). In the subgame starting
with player 1 c hoosing bet ween and ,part(a)aboveshowedthatthe
unique (non-degener ate) mixed strategy Nash equilibriu m was ( )=
(
1
2
5
8
) with expected payoffsof(
1
2
)=(
5
4
1). If this will be pla y ed by
the pla yers after pla yer 1 c hooses , then pla yer 1’s best reply at the
root is indeed to ch oose because
5
4
1. Hence, as suggested earlier,
player 1 choosing followed by the mix ed strategy Nash eq uilib riu m
( )=(
1
2
5
8
) is also a subgame perfect N ash equilib rium. ¥
6. Inv e stment in the Future: Consider tw o firms that pla y a Cournot com-
petition game w ith demand =100− , and costs for each firm giv en b y
(
)=10
.Imaginethatbeforethetwofirms play the Cournot game, firm
1 can invest in cost reduction. If it invests, the costs of firm 1 will drop to
1
(
1
)=5
1
. The cost of investment is 0. Firm 2 does not hav e this
investment opportunity.
(a) Find the value
∗
forwhichtheuniquesubgameperfectequilibrium
involves firm 1 investing.
Answ er: If firm 1 does not invest then they are expected to pla y the
Courn ot Nash equilibrium wh ere both firms ha ve costs of 10
.Each
firm solves,
max
(100 − (
+
) − 10)
which leads to the first order condition
90 −
− 2
=0
yielding the best response function
(
)=
90 −
2
and the unique Courn ot Nash equ ilibr ium is
1
=
2
=30with profits
1
=
2
=900.Iffirm 1 does invest then for firm 1 the problem becomes
max
1
(100 − (
1
+
2
) − 5)
1
8. Credibility and Sequential Rationality 143
which leads to the best response function
1
(
2
)=
95 −
2
2
For firm 2 the best response function remains the same as solved earlier
with costs 10
2
, so the unique Cournot Nash equilibriu m is now solved
using both equations,
1
=
95 −
90−
1
2
2
which yield s
1
=
100
3
,
2
=
85
3
,andprofits are
1
=1 111
1
9
while
2
= 802
7
9
. H ence, the increase in pro fits from the equilibrium with
investmentforplayer1are
∗
=1 111
1
9
−900 = 211
1
9
,whichisthemost
that player 1 would be willing to pay for the in vestment anticipating that
they will play the Courn ot Nash equilibrium after any choice of player
1 regar ding in vestment. If
∗
then the unique subgame perfect
equilib riu m is that first, player 1 in vests, then they players choose
1
=
100
3
,
2
=
85
3
, and if pla yer 1 did not invest the payers choose
1
=
2
=30.
(Notethatif
∗
then the unique subgame perfect equilibrium is
that first, player 1 does not invest, then they players choose
1
=
2
=
30, and if player 1 did invest the pa yers choose
1
=
100
3
,
2
=
85
3
.) ¥
(b) Assume that
∗
. Find a Nash equilibrium of the game that is not
subgame perfect.
Answ er: We construct a Nash equilibrium in which player 1 will invest
despite
∗
. Player 2’s strategy will be, play
2
=
85
3
if pla yer 1
inv e sts, and
2
=100if he does not invest. With this belief, if play er 1
does not inv est then he expects the price to be 0, and his best response
is
1
=0leadingtoprofits
1
=0. If he in vests then his best response
to
2
=
85
3
is
1
=
100
3
, which togeth er ar e a N a sh eq uilibr ium in the
Cournot game after in v estmen t. For an y 1 111
1
9
this will lead to
positive profits, and hence, for
∗
1 111
1
9
the strategy of pla yer 2
described abo ve, together with pla yer 1 choosing to invest, play
1
=
100
3
if he invests and
1
=0if he does not is a Nash equilibrium . It is not
144 8. Credibility and Sequential Rationality
subgam e perfect because in the subgame follo w ing no in vestment, the
pla yers are not play ing a Nash equilibrium. ¥
7. Debt and Repayment: A project co sting $100 yields a gross return of
$110. A lender (player 1) is approac hed by a debtor (player 2) requesting a
standard loan con tra ct to complete the project. If the lender chooses not to
offer a loan, then both parties earn nothing. If the lender c hooses to offer
a loan of $100, the debtor can realize the projects gains, and is obliged by
con tract to repay $105. For simplicity, assume that money is continuous, and
that the debtor can choose to return an y amount of m on ey ≤ 110.Also,
ignorethetimevalueofmoney.Assumefirst that no legal system is in place
that can cause the lender to repay, so that default on the loan (less than full
repa ym ent) carries no repercussions for the deb tor.
(a) Model this as an extensive form game tree as best as you can and find
a subgame perfect equilibrium of this game. Is it unique?
Answ er: Pla yer 1 has t wo cho ices first, lend ()ordon’tlend().
After both play ers get zero, while after player2choosesavalue
∈ [0 110] to repay. The game can be described as follo w s:
There is a unique subgame perfect equilibrium . If player 2 is offered the
loan then he suffers no penalty from repaying, and his best response is
to choose =0. Anticipat in g this behavior player 1 should c hoose .
¥
8. Credibility and Sequential Rationality 145
(b) No w assume that there is a legal system in place that allow s the lender
to voluntarily choose whether to sue or not to sue wh en the debtor de-
faultsandrepaysanamount105. Furtherm ore, assume that it is
costless to use the legal system (it is supplied b y the state), and if the
lender sues a debtor that defaulted, the lender will get the $105 repaid
in full. After paying the lender, the borrow er will pay a fine of $5 to the
court above and beyond the repayment. Model this as an extensiv e form
game tree as best as you can and find a subgame perfect equilibrium of
this game. Is it unique?
Answ er: Th e game no w distinguished bet ween two conditions: ≥ 105
in which case it is like the game in part (a) above, and 105 in which
case player 1 has a new decision node where he can ch oose to sue ()
or not sue ().
Starting at the last decision node of player 1, because it is relevan t only
when 105, it follow s that −100 5 implying that dominates .
Anticipatin g this, pla yer 2’s best response in the repa y m ent phase is to
choose = 105 This is the lowest paym ent that does not trigger a suit.
At the root of the tree player 1 anticipa tes a pa yoff of 105−100 = 5 0
and hence prefers to c hoose . The resulting outcome yields the pa yoffs
146 8. Credibility and Sequential Rationality
(5 5) This backward ind uctio n arg u ment shows tha t this is the unique
subgame perfect equilibriu m . ¥
(c) Are there Nash equilibria in the game described in (b) abo ve that are
not subgame perfect equilibria?
Answ er: For player 1, ch oosing followed by is a domina nt strategy
becauseitguarantieshimapayoff of at least 5 (exactly 5 when 105
and −100 when ≥ 105.) Given this strategy, pla yer 2’s best reply is
to c h oose =105. Hence, the only Nash equilibrium is also the subgam e
perfect Nash equilib rium. ¥
(d) No w assume that using the legal system is costly: if the lender sues,
he pays la wyers a legal fee of $105 (this is the lawy ers price whic h is
unrelated to the con tract above). The rest proceeds the sam e as before
(if the lender sues a debtor that defaulted , the lender will get repaid in
full; after pa yin g the lender, the borrower will pay a fine of $5 above
and bey o nd the repa ym ent.) Model this as an extensiv e form game tree
as best as y ou can and find a subgame perfect equilibrium of this game.
Is it unique?
Answ er: Thegameisnow,
Because − 100 ≥−100 it follows that tha t is w eakly dominated by
8. Credibility and Sequential Rationality 147
. A nticipatin g this, player 2’s best response in the repaym ent phase
is to c hoose =0 At the root of the tree player 1 an ticipates a payoff
of −100 0 and hence prefers to ch oose , and the outcom e results in
pa y offs (0,0). This backward induction argumen t show s that this is the
unique subgame perfect equilibrium. ¥
(e) Are there Nash equilibria in the game described in (d) abo ve that are
not subgame perfect equilibria?
Answ er: There are infinitely many . Any choice by player 2 of ≤ 100,
for which play ing is a best res ponse, will be a Nash equilibrium in
which pla yer 2 is not pla yin g a best response. ¥
(f) Now assume that a law change is proposed: upon default, if a debtor is
sued he has to first repa y the lender $105, and then pay the legal fees
of $105 abo ve and beyond repa yment of the loan, a nd no extra fine is
imposed. Should the lender be willing to pay for this la w c h ange ? If so,
ho w m uch?
Answ er: Thegameisnowasfollows:
Thebackwardinductionargumentfollowsthesamelogicasinpart(b)
resulting in the outco m e (5 5). This yields player 1 an extra pay o ffsof
5 relative to the solution in part (d), implying that he should be willing
to pay up to 5 in order to ha ve the law implemented. ¥
148 8. Credibility and Sequential Rationality
(g) If you were the “social planner”, w ould you implemen ted the suggested
law?
Answ er: Yes because it results in a Pareto superior outcome of (5 5)
instead of (0 0). ¥
8. En try Deterrence 1: NSG is considering en try into the local phone market
in the Ba y Area. The incumbent S&P, p redicts that a price w ar will result
if NSG enters. If NSG stays out, S&P earns monopoly profits valued at $10
million (net present value, or NPV of profits), while NSG earns zero. If NSG
enters, it must incur irrev ersible en tr y costs of $2 million. If there is a price
war, each firm earns $1 million (NPV) . S&P alw ays has the option of accom-
modating en t ry (i.e., not starting a price war). In such a case, both firm s
earn $4 million (NPV ). Suppose that the timing is such that NSG first has
to choose whether or not to enter the market. Then S&P decides whether
to “accommodate entry” or “engage in a price w ar.” What is the subgame
perfect equilibrium outc om e to this sequential game? (Set up a gam e tree.)
Answ er: Letting NSG be play er 1 and S&P be player 2,
Backward induction implies that player 2 will Accom m odate, and player 1
will therefore enter. Hence, the unique subgam e perfect equilibrium is (En-
ter,Accom m odate). ¥
9. En try Deterrence 2: Consider the C ourn ot duopoly game with dem and
=100− (
1
+
2
), and variab le costs
(
)=0for ∈ {1 2}.Thetwistis

8. Credibility and Sequential Rationality 149
that there is now a fixed cost of production 0 that is the sam e for both
firm s.
(a) Assume firstthatbothfirms choose their quantities simultaneou sly.
Model this as a normal form game.
Answ er: This is a standard Cournot game with two play ers: =
{1 2}
= R
+
(the non-negativ e real line) and w e need to add the
fixed costs to the pa yoff function ,
(
1
2
)=(100−
1
−
2
)
− for
∈ {1 2}.
(b) Write dow n the firm’s best response function for = 1000 and solv e for
pure strategy Nash equilibrium . Is it unique?
Answ er: Because the fixed costs do not affect the first order conditions,
from section 5.2.3 we know that the two best response functions ignor ing
the fixed costs are,
(
)=
100 −
2
.
With fixed costs, howev er, each firm will produce only if it has positiv e
profits. For example, using firm 1’s best response function , its pro fits
conditional on pla ying a best response are
1
(
1
(
2
)
2
) = (100 − (
100 −
2
2
+
2
))
100 −
2
2
−
=2500+
2
2
4
− 50
2
−
=1500+
2
2
4
− 50
2
where the last inequality follo w s from =1000. Now w e can compute
the value of
2
for w hich playin g a best response by firm 1 w ill yield
zero profits, which in turn w ill imply that for higher levels of
2
firm
1 will incur a loss even when it plays a best response conditional on
producing. We have,
1500 +
2
2
4
− 50
2
≥ 0

150 8. Credibility and Sequential Rationality
which holds when
2
≤ 100 − 20
√
10 ≈ 3675. A symmetric argumen t
will hold for fir m 2, which yields the best response function with a fixed
cost of =1000to be,
(
)=
(
100−
2
if
≤ 100 − 20
√
10
0 if
100 − 20
√
10
.
Using the first portion of the best response function to try and solve for
a Nash equilibriu m , we obtain that
1
=
2
=33
1
3
3675.Thus,when
=1000,
1
=
2
=33
1
3
is the unique Nash equilib rium of this game.
¥
(c) No w assume that firm 1 is a “Stackelberg leader” in the sense that it
moves first and chooses
1
, and then after observing
1
firm 2 c hooses
2
. Also assume that if firm 2 cannot make strictly positive profits then
it will not produce at all. Model this as an extensive form game tree as
best as you can, and find a subgame perfect equilibrium of this game
for =25.Isitunique?
Answ er: similar to the analysis in section 8.3.2 we kno w that, ignorin g
fixed costs, firm 2 will choose
2
(
1
)=
100−
1
2
as derived above. With
=25it will not produce for so m e valu es of
1
close to 100 (Similar
to the ana lysis in p ar t (b),
1
must satisfy 2500 +
2
1
4
− 50
1
− 0
with =25. Th i s will be sat is fied when
1
≤ 90.) Given firm 2’s best
response, firm 1 maxim izes
max
1
(100 −
1
−
100 −
1
2
)
1
− 25
which yields the first order condition 50 −
1
=0or
∗
1
=50. Because
∗
1
90 we know that firm 2 will indeed follow
2
(
1
)=
100−
1
2
=25,
profits for firm 1 are
1
=25× 50 − 25 = 1 225,andforfirm 2 are
2
=25× 25 − 25 = 600. By construction, this is the unique subgame
perfect equilib riu m. ¥
(d) Ho w does your answ er in (c) c hange for =725?
Answ er: Now firm 2 will follo w
2
(
1
)=
100−
1
2
as long as 1775 +
2
1
4
−

8. Credibility and Sequential Rationality 151
50
1
≥ 0, which holds for
1
≤ 100 −10
√
29 ≈ 4615.Aswesawinpart
(c), if firm 1 ant icipates firm 2 to produce according to
2
(
1
)=
100−
1
2
then firm 1 produces
∗
1
=50. It turns out that if firm 1 anticip ates firm
2 to stay out then it will also produce
∗
1
=50which is the monopolists
optim al choice for this market w ith only fixed costs. Ho wev er, since
50 4615 this c h oice will indeed cause firm2tostayout,andthe
unique subgame perfect equilibrium is no w
∗
1
=50and
2
(
1
)=
(
100−
1
2
if
1
≤ 100 − 10
√
29
0 if
1
100 − 10
√
29
,
resulting in
∗
2
=0. ¥
10. Playing it safe: Consider the following dynamic game: Play er 1 can choose
toplayitsafe(denotethischoiceby), in whic h case both he and play er 2 get
a payoff of 3 eac h , or he can risk playing a game with pla yer 2 (den ote this
choice by ). If he chooses , then they play the following simultane ou s
mo ve game:
player 1
Play er 2
8 0 0 2
6 6 2 2
(a) Dra w a game tree that represen ts this gam e. Ho w many proper sub-
gamesdoesithave?
Answ er:

152 8. Credibility and Sequential Rationality
The game has t wo proper subgames: the whole game and the subgame
starting at the node where 1 ch ooses between and . ¥
(b) Are there other gam e trees that would work? Explain briefly.
Answ er: Yes - it is possible to have player 2 move after 1’s initial move,
and then have player 1 w ith an inform a tion set as follows:
(c) Construct the matrix represen tation of the norma l form of this dynamic
game.

8. Credibility and Sequential Rationality 153
Answ er: The game can be represen ted by the following ma trix,
Player 1
Play er 2
8 0 0 2
6 6 2 2
3 3 3 3
3 3 3 3
¥
(d) Find all the Nash and subgame perfect equilibr ia of the dynam ic gam e.
Answ er: It is easy to see that there are t wo pure strategy Nash equi-
libria: ( ) and (). It follows immediately that there are infi-
nitely m any mixed strategy Nash equilibria in whic h play e r 1 is mixing
between and in an y arbitrary w ay and player 2 chooses .Itis
also easy to see that follo w ing a c ho ice of , there is no pure strategy
Nash equilibriu m in the resultin g subga m e. To find the mixed strategy
Nash equilibriu m in that subga m e, let pla yer 1 choose with proba-
bility and with probabilit y (1 −), and let player 2 ch oose with
probab ility . For pla yer 2 to be indifferentitmustbethat
(0) + (1 − )(6) = (2) + (1 − )(2)
and the solution is =
2
3
. Similarly, for player 1 to be indifferentitmust
be that
(8) + (1 − )(0) = (6) + (1 − )(2)
and the solution is =
1
2
. Hence, ( )=(
1
2
3
5
) is a mixed strateg y
Nash equilibriu m of the subgame after play er 1 chooses , yield in g
expected payoffsof(
1
2
)=(4 2). In an y subgame perfect equilibrium
the players will have to pla y this mixe d strateg y equilib rium follo w in g
,andbecause4 3 player 1 will prefer over . Hen ce, ch oosing
follo wed by the m ixed strategy com puted abo ve is the unique subgame
perfect equilib riu m. ¥
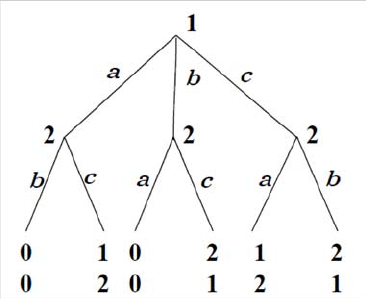
154 8. Credibility and Sequential Rationality
11. RA Sele ction with a Tw ist:Twostaff managers in the ΠBΦ sororit y, the
house manager (player 1) an d kitch en manager (player 2), a re supposed to
select a residen t assistan t (RA) from a pool of three candidates: { }.
Play er 1 prefers to and to . Play e r 2 prefers to and to .The
process that is imposed on them is as follo w s: First, the house manager vetoes
one of the candidates, and announces the v eto to the central office for staff
selection, and to the kitchen m a nager. Next, the kitchen manager vetoes
one of the remaining two candidates and announ ces it to the cen tr al office.
Finally, the director of the central office assigns the remaining candida te to
be an RA at ΠBΦ.
(a) Model this as an exten sive form ga m e (usin g a gam e tree) wh ere a
player’s most preferred candidate gives a payoff of 2, the second gives a
pa y off of 1, and the last giv es 0.
Answ er: Since first player 1 effectively removes a candidate, each of
the three choices (to v eto) of player 1 are followed b y two possible veto
c hoices of play er 2:
¥
(b) Find the subgame perfect equilibria of this gam e. Is it unique?
Answ er: If player 1 vetoes or then player 2 will veto , and if play er 1
vetoes then player 2 will v eto . By bac kward induction, an ticipating
player 2’s behavior play er 1 will v eto candidate . This is the unique
8. Credibility and Sequential Rationality 155
subgam e perfect equilibrium by bac kward induction resulting in pa yoffs
of (2 1). ¥
(c) Are there Nash Equilibria that are not subgame perfect equilibria.
Answ er: Yes. Play er 2 can threaten to veto candidate whenever player
1 vetoes either or , and v eto candidate when player 1 v etoes .Player
1’s best reply to this strategy is to veto either or . The players will
both be playin g best responses on the equilibrium path but play er 2
is not pla ying a best response follo wing the c hoice of pla yer 1 to veto
candidate . Hence, this is a Nash equilibrium that is not subgam e
perfect.
(d) No w assume that before the t wo players play the gam e, player 2 can
send an alienating E-mail to one of the candidates, which would result
in that candidate withdrawing her application. Would player 2 ch oose
to do this, and if so, with wh ich candidate ?
Answ er: Player 2 would lik e to send the email to candidate .That
way, only candidates and will be in the pool and both players will
veto ,resultinginthepayoffs (1 2) which are better for player 2 than
theuniquesubgameperfectequilibriumpayoffs derived in part (a). ¥
12. Agenda Setting: An agenda-setting game is described as follow s. The “issue
space” (set of possible policies) is an int erval =[0 5].AnAgendaSetter
(player 1) proposes an alternative ∈ against the status quo =4.
Afterplayer1proposes, the Legislator (player 2) observ es the proposal
and selects between the proposal and the status quo . Player 1’s most
preferred policy is 1 and for any final policy ∈ his pa yoff is given by
1
()=10− | − 1|
where | −1| denotes the absolute v alue of ( −1). Player 2’s most preferred
policy is 3 and for any final policy ∈ her pay off is given by
2
()=10− | − 3|
156 8. Credibility and Sequential Rationality
That is, each player prefers policies that are closer to their m ost preferred
policy.
(a) Write the game down as a normal form game. Is this a game of perfect
or imperfect information?
Answ er: There are two players, ∈ {1 2} with strategy sets
1
= =
[0 5] and
2
= { } where denotes accepting the proposal ∈
and means rejecting it and adopting the status quo =4. The pay offs
are giv en by
1
(
1
2
)=
(
10 − |
1
− 1| if
2
=
7 if
2
=
and
2
(
1
2
)=
(
10 − |
1
− 3| if
2
=
9 if
2
=
(b) Find a sub game perfect equilibrium of this gam e. Is it uniqu e?
Answ er: Pla yer 2 can guarantee himself a payoff of 9 by choosing ,
implying that his best response is to c h oose if and only if 10−|
1
−3| ≥
9, which will ho ld fo r any
1
∈ [2 4]. Player 1 would like to have an
alternative adopted that is closest to 1, which im plies that his best
response to pla yer 2’s sequentially rational strategy is to ch oose
1
=2.
This is the unique subgame perfect eq uilibriu m which results in the
pa y offsof(
1
2
)=(9 9). ¥
(c) Find a Nash equilibrium that is not subga m e perfect. Is it un ique? If
y e s, explain. If not, sho w all the Nash equilibria of this game.
Answ er: One Nash equilib rium is where pla yer 2 adopts the strategy
“I will reject anything except
1
=3”Ifplayer1chooses
1
=3then
his pay off is 8, while an y other choice of
1
is expected to yield player
1apayoff of 7. H en ce, player 1s best response to pla yer 2’s proposed
strategy is indeed to c h oose
1
=3and the payoffsfromthisNash
8. Credibility and Sequential Rationality 157
equilib riu m are (
1
2
)=(8 10). Since pla yer 2 can guaran tee himself
apayoff of 9,thereareinfinitely many Nash equilibria that are not
subgam e perfect and that follow a similar logic: player 2 adopts the
strategy “I will reject an ything except
1
= ”forsomevalue ∈ (2 4).
Play er 1 wou ld strictly prefer the adoption of over 4, and hence would
indeed propose , and player 2 would accept the pro posal. For =4
both players are indifferent so it w o uld also be supported as a Nash
equilib r iu m . ¥
13. Ju n k Ma il Advertisin g: Suppose there is a single good that is owned b y a
single seller who values it at 0 (he can consume the good and get a pay off
of ). There is a single buyer who has a small transportation cost 0 to
get to an d back from the seller’s store, and he values the good at + .
The buyer first decides whether to make the comm ute or stay at home, not
buy the good and receive a pa yoff of 0. If the buy ers commutes to the store,
the seller can then mak e the buyer a Take-It-Or-Lea ve-It price offer ≥ 0.
The buy er can then accept the offer, pay andgetthegood,orhecanwalk
out and not buy the good. Assume that and , are common kno w ledg e.
(a) As best as you can, dra w the extensive form of this gam e. What is the
best response of the buy er at the node where he decides whether to
accept or reject the seller’s offer?
Answ er: Letthebuyerbeplayer1.Denoteby goingtothestoreand
sta y ing home, and by accepting or rejecting the seller’s offer.
The game can be described as follo w s:T he best response of player 1 after
the offer is to c h oose if and only if − − ≥− or ≤
. ¥
(b) Find the subgam e perfect equilibrium of the game and show that it is
unique. Is it P areto Optimal?
Answ er: Given the buyer’s best response at the accept/reject node,
backward induction implies that the seller’s unique best response is to
offer = because + . An ticipa ting this, the buy er knows
that if he chooses then his payoff will be −, so his unique best
158 8. Credibility and Sequential Rationality
FIGURE 8.1.
response is to choose and the pa y offs from the unique subgame perfect
equilib riu m are (
1
2
)=(0). This outcome is not P areto optimal
because if the t wo play ers trade at an y price such that −
then they w o uld both be better off. ¥
(c) Are there Nash equilibria that yield a higher pa yoff to both pla yers as
compared to the subgame perfect equilibrium y ou found in (b) abo ve?
Answ er: There are infinitely many suc h Nash equilibria. Fix some
∗
∈
( − ) and let player 1’s strategy after the proposal stage be “I w ill
accept an y offer ≤
∗
and reject anything else.” Giv en this strategy,
and giv en that
∗
, player 2’s best response is to offer
∗
and pla yer
1 will therefor e wish to choose because
∗
− Th e resulting
pa y offs will be (
1
2
)=( −
∗
−
∗
) (0). ¥
(d) No w assume that before the game is played, the seller can, at a small
cost ( − − ) send the buyer a postcard that commits the seller
to a certain price at whic h the buyer can buy the good (e.g., “bring this
coupon and get the good at a price ”). Would the seller choose to do
so? Justify y ou r answer with an equilibrium analysis.
Answ er: Th e seller wou ld inde ed ben e fit from sending such a postcard.

8. Credibility and Sequential Rationality 159
To see this, let = −− −0 and imagine that the seller sends he
postcard with a price
∗
= − −
2
. The buy er wh o receiv es this card
kno w s that he can go to the store at a cost of and pay
∗
for the good
which w ou ld lea ve the buyer with a payoff of
1
= − −
∗
=
2
0,
and hence w o uld prefer to go shoppin g. The seller would receive a pa yoff
of
2
=
∗
− = +
2
, which is better than no trade. This w ould
work for any price
∗
= − − for any ∈ (0 1). ¥
14. Hy perbolic Discounting: Consider the three period example of a player
with hyperbolic discou nting described in section 8.3.4 with ln() utility in
eac h of the three periods and with discoun t factors 0 1 and 0 1.
(a) Solv e the optimal choice of player 2, the second period self, as a function
of his budget
2
, and .
Answ er: Player 2’s optimization problem is given b y
max
2
2
(
2
−
2
)=ln(
2
)+ ln( −
2
)
for which the first order condition is
2
2
=
1
2
−
2
−
2
=0
which in turn imp lies that player 2’s best response function is,
2
(
2
)=
2
+1
,
which leav es
3
=
2
−
2
(
2
)=
2
+1
for consum ption in the third
period. ¥
(b) Solve the optimal c hoice of player 1, the first period self, as a function
of , and .
Answ er: Pla yer 1 decides how much to allocate between his o wn con-
sump tion and that of pla yer 2 taking into account that
2
(
2
)=
2
+1
,
hence player 1 solv es the follo w ing proble m ,
max
1
1
(
1
−
1
+1
( −
1
)
+1
)=ln(
1
)+ ln(
−
1
+1
)+
2
ln(
( −
1
)
+1
)
160 8. Credibility and Sequential Rationality
for which the first order condition is,
1
1
=
1
1
−
−
1
−
2
−
1
=0
which in turn imp lies that player 1’s best response function is,
1
()=
+
2
+1
.
¥
15. Time Inconsistency: Consider the three period example of a player with
h y perbolic discoun ting described in section 8.3.4 with ln() utility in eac h of
the three periods, with initial bud get and with discount factors =1and
=
1
2
.
(a) Solve the optimal plan of action of a “naiv e” pla yer 1 who does not tak e
into account ho w his future self, pla y er 2, will alter the plan. What is
player 1’s optimal plan
∗
1
,
∗
2
and
∗
3
as a function of ?
Answ er: Anaiveplayer1willsolve,
max
2
3
( −
2
−
3
2
3
)=ln( −
2
−
3
)+ ln(
2
)+
2
ln(
3
)
=ln( −
2
−
3
)+
1
2
ln(
2
)+
1
2
ln(
3
)
when =
1
2
and =1.Thetwofist order conditions are,
2
= −
1
−
2
−
3
+
1
2
2
=0
and,
3
= −
1
−
2
−
3
+
1
2
3
=0
Solving these two equatio ns yields the solution
2
=
3
=
4
and using
1
= −
2
−
3
gives,
1
=
2
¥
8. Credibility and Sequential Rationality 161
(b) Let
2
betheamountleftfromthesolutiontopart(a)aboveafter
player 1 consumes his planned choice of
∗
1
.Given
2
, what is the opti-
mal plan of player 2? In what way does it differ from the optimal plan
set out by player 1?
Answ er: This w as solv ed at the bottom of page 168 in the textbook.
Afterplayer1leave
2
for player 2, his optimization problem is giv en
by
max
2
2
(
2
2
−
2
)=ln(
2
)+
1
2
ln( −
2
)
for which the first order condition is
2
2
=
1
2
−
1
2(
2
−
2
)
=0
which in turn imp lies that player 2’s best response function is,
2
(
2
)=
2
2
3
,
which lea v es
3
=
2
−
2
(
2
)=
2
3
for consumption in the third
period. From part (a) w e kno w that
2
=
2
so player 2 will c h oose
2
=
3
and
3
=
6
. This is in contrast to what player 1 planned which
was
2
=
3
=
4
so pla yer 2 is o verconsuming relativ e to what player
1wouldhavewanted.¥
16. The Value of Commitmen t: Consider the three period example of a player
with hyperbolic discou nting described in section 8.3.4 with ln() utility in
eac h of the three periods and with discount facto rs =1an d =
1
2
.We
solved the optimal consump tio n plan of a sophisticat ed player 1.
(a) Imagine that an external entit y can enforce any plan of action that
player 1 chooses in =1and will prevent player 2 from modifying it.
W ha t is the plan that player 1 wou ld c h oose to enforce?
Answ er: Player 1 wants to maximize,
max
2
3
( −
2
−
3
2
3
)=ln( −
2
−
3
)+ ln(
2
)+
2
ln(
3
)
=ln( −
2
−
3
)+
1
2
ln(
2
)+
1
2
ln(
3
)

162 8. Credibility and Sequential Rationality
when =
1
2
and =1.Thetwofist order conditions are,
2
= −
1
−
2
−
3
+
1
2
2
=0
and,
3
= −
1
−
2
−
3
+
1
2
3
=0
Solving these two equatio ns yields the solution
2
=
3
=
4
and using
1
= −
2
−
3
gives,
1
=
2
Th us, pla y er 1 would c hoose to enforce
1
=
2
and
2
=
3
=
4
. ¥
(b) Assume that =90. Up to ho w m uch of his initial budget will player
1 be willing to pay the external entity in order to enforce the plan you
found in part (a)?
Answ er: If the external en tit y does not enforce the plan, then from the
analysis on pages 168-169 we know that pla yer 2 will choose
2
=
3
=30
and
3
=
6
=15, and player 1 will choose
1
=
2
=45. The discounted
value of the stream of pa yoffs for pla yer 1 from this outcome is therefore,
ln(45) +
1
2
ln(30) +
1
2
ln(15) ≈ 686
If, however, pla yer 1 can have the plan in part (a) abov e enforced then
his discoun ted value of the stream of payoffsis
ln(45) +
1
2
ln(225) +
1
2
ln(225) ≈ 692
We can therefore solv e for the amount of budget =90that pla yer
1 w ou ld be willing to give up whic h is found b y the follo w ing equality,
ln(45 − )+
1
2
ln(225) +
1
2
ln(225) = 686
whic h yields ≈ 263 Hence, pla yer 1 will be willing to giv e up to 263
of his initial budget =90in order to enforce the plan
2
=
3
=
4
=225. ¥

This is page 163
Printer: Opaque
t
9
Mu lti-S t a ge G a mes
1. Consider the following sim u ltan eou s mo ve game that is played tw ice (the
play er s observe the first period outcome prior to the second period pla y):
pla yer 1
Play er 2
10,10 2,12 0,13
12,2 5,5 0,0
13,0 0,0 1,1
(a) Find all the pure strategy subgam e perfect equilibria with no discount-
ing ( =1). Be precise in defin ing history conting ent strategies for both
pla yers.
Answ er: The simultaneous mo ve gam e has t wo pure strategy Nash
equilib r ia : ( )and( ), whic h implies that one of these has to be
pla yed in the second stage of the game. We kno w that an y unconditional
play of these Nash equilibria in each stage is a subgame perfect equilib-
rium of the m ultistag e game im plyin g four pure strategy Nash equilib ria
(e.g., pla yer 1 pla y s follo wed by regardless of what pla yer 2 chose
and player 2 plays fo llow ed b y regardless of what pla yer 1 did.)

164 9. Multi-Stage Games
We now construct other equilibria that are history conting ent in which
the pla yers will pla y the “reward” ( ) in the second period if they
followed t h e first period proposed strategies giving each a p ayoff of 5,
while they will play the “punishment” () if one of the players de-
viated from the proposed strategy and both will receiv e a pa yoff of 1.
Note that the loss from not follow ing the first stage proposed strategies
will be 5 − 1=4in the second period, and because =1th en 4 is
also the discounted loss. It is therefore possible to support any pa y off
in the first stage for whic h the best deviation is no greater then 4 with
=1because the discounted loss from the second stage “punishm ent”
would be greater than the first period gain. The only pair of pay o ffs
from which there is a greater gain than 4 is from (0 0) because one
of the players can deviate to (5 5). Hence, pick any pure strategy pair
( ) that is not ( ) or (). The follow ing is a subgame perfect
equilib r iu m: pla yer 1 plays in the first stage followed by if ( )
was followed and if it was not. Sim ilarly, player 2 plays in the first
stage follo wed b y if ( ) was followed and if it w as not. For =1
this is a subg a me perfect equilibriu m. ¥
(b) For each of the equilibria y o u found above, find the smallest discoun t
factor that supports it.
Answ er: The four subgame perfect equilibria that are just an uncon-
ditional sequence of one-stage Nash equilibria are equilibria for any dis-
count factor. The others, however, must guarantee that the discoun ted
loss from punishmen t is greater than the first period gain for the player
whohasthemosttobenefit from the deviation. For the first stage
outcomes ( ) ∈ {() () ( }, the pla y er who gains most
can gain 3, and hence the discoun t factor must satisfy the inequal-
it y 3 − 4 ≤ 0 or ≥
3
4
for these outcomes to be pla yed in the first
stage of the subgame perfect equilibrium. For the other two possibili-
ties, ( ) ∈ {( ) ()} theplayerwhogainsmostcangainonly1,
andhencethediscountfactormustsatisfytheinequality1 − 4 ≤ 0 or

9. Multi-Stage Games 165
FIGURE 9.1. The Cen tipede Game
≥
1
4
for these outcomes to be played in the first stage of the subgame
perfect equilib riu m. ¥
2. Cen tipedes revisited: Two players are playing two consecutive games.
First, they play the cen tipede game described in Figur e 9.1. After the cen-
tipede game they play the follo wing coordination game:
Player 1
Player 2
1 1 0 0
0 0 3 3
(a) What are the Nash equilibria of each stage game?
Answ er: The first stage game has a unique Nash equilibrium outcome
in which player 1 plays in the first stage and payoffsare (1 1).This
can be supported in more than one M ash equilibrium (fo r ex am p le,
player 1 plays alw ays and player 2 does as w ell, which is the subgame
perfect equilibrium, or player 1 player always and player 2 plays
first and later — there are more.) The second stage game have three
Nash equilibria. The t wo pure are ( ) and ( ) and the mixed one
has player 1 (respectively 2) play (respectiv ely ) with probability
3
4
.
¥
(b) Ho w man y pure strategies does each pla yer ha ve in the m ultistage game?
Answ er: The players have four pure strategies in the first stage game
166 9. Multi-Stage Games
(t wo information sets with t wo actions in each). The second stage strate-
gies can be conditional on the outcomes of the first stage, of which there
are4.(Wearedefining an outcome is the pa y offsofthefirst stage and
not the strategies that players c h ose to obtain the payoffs. Unlike a ma-
trix game, these will be different here because, as we sa w in part a.
above, there are differentcombinationsofpurestrategiesthatcanlead
to the same outcome.) Hence, there are 2
4
=16pure strategies for each
pla yer in the second stage, which can follo w each of the 4 first stage
pure strategies, giving every pla yer a total of 64 pure strategies. ¥
(c) Find all the pu re strategy subgame perfect equilibria with extreme dis-
counting ( =0). Be precise in defining history contingent strategies for
both pla yers.
Answ er: In the second stage the pla yers m u st play either ( ) or
( ) for any history. With extreme discoun ting we cannot support
play in the first stage that is not a Nash equilibrium because there is no
second stage “punishment” that can deter first stage deviations. Hence,
in the first stage the pla yers must play a subgame perfect equilibrium
of the first stage game whic h is alw a ys for pla yer 1 and always for
pla yer 2. Hence, there are t wo possible outcomes that can be supported
b y a subgame prefect equilibrium, (1 1) followed b y (1 1) or by (3 3).
Ho w ever, there are 2
4
=16pure strategy subgam e perfect equilibria
because for each of the 4 outcomes of the first stage th e players m u st
specify which of the 2 equ ilib r ia ( ) or () will be pla y ed in the
second stage. ¥
(d) No w let =1. Fin d a subgam e perfect equilibrium for th e two-stag e
game in w hich the players receiv e the payoffs(2 2)inthefirst stage-
game.
Answ er: To get (2 2) in the first stage pla yer 2 m ust overcome the
temp tation to choose at his firstmoveandget3 instead. Hence, w e
can use the follo w ing conditional strategies in the second stage: player 1
(respectiv ely 2) pla ys (respectively )iftheoutcomeofthefirst stage

9. Multi-Stage Games 167
was (2 2) while they play and otherwise. In the first stage player 1
will pla y followed by a nd player 2 will play followed by .Player
1 has no reason to deviate in the first stage, and neither does player 2
because the gain of 1 from deviating in the first stage is less than the
loss of 2 in the second stage. ¥
(e) What is the lo west value of for which the subgame perfect equilibriu m
y ou found in (d) survives?
Answ er: The pain from deviation will de ter pla yer 2 if and o nly if
1 − 2 ≤ 0 or ≥
1
2
. ¥
(f) For greater than the value y ou found in (e) abov e, are there other
outcomes of the first stage cen tipede game that can be supported as
part of a subgame perfect equilibrium?
Answ er: Yes — the exact same idea can be used to support any of the
other outcome s because the player who is tempted to deviate will gain
1inthefirst period. ¥
3. Campaigning Adds: Two political candidates are sc hedu led to campaign
in two states, in one in period =1andintheotherin =2. In each state
they can either choose a positiv e campa ign that promotes their ow n agenda
( for pla yer 1, forplayer2)oranegativeonethatattackstheiropponent
( for player 1, forplayer2).Residentsofthefirst period state do not
mind negative campaigns, which are generally effective, and payoffsinthis
state are given by the follow ing matrix:
Play er 1
Play er 2
2 2 0 5
5 0 3 3
168 9. Multi-Stage Games
In the second period state, residen ts dislike negative campaign s despite their
effectiv en ess and the payoffs are given b y the follo w ing matrix:
Play er 1
Play er 2
6 6 1 0
0 1 2 2
(a) What are the Nash equilibria of e ach stage game? Find all the pure
strategy subgame perfect equilibria with extrem e discounting ( =0).
Be precise in definin g history con ting ent strategies for both players.
Answ er: The first stage game has a unique dom inant strategy N ash
equilib r iu m () while the second stage game has two pure strategy
equilib r ia , ( ) and () and a mixed strategy equilibrium in which
each player c hooses the positive campa ign with probab ility
1
5
. In the sec-
ond stage the pla yers must play either ( ) or ( ) for any history in
a pure strategy subgam e perfect equilibrium. With extreme discounting
w e cannot support play in the first stage that is not a Nash equilib-
rium because there is no second stage “punishm ent” that can deter first
stage deviations. Hen ce, in the first stage the pla yers must play ( ).
Hence, ( ) follo wed by either ( ) or ( ) will be the only out-
comes that can be supported as subg am e perfect equilibria. Howev er,
there are 2
4
=16pure strategy subgame perfect equilibria because for
each of the 4 outcomes of the first stage the players m ust specify wh ich
of the 2 equilibria ( ) or ( ) will be played in the second stage. ¥
(b) No w let =1. Fin d a subgam e perfect equilibrium for th e two-stag e
game in which the play ers c hoose ( )inthefirst stage-game.
Answ er: We can use the conditional second stage strategies in whic h
pla yer 1 (respectiv ely 2) plays (respectively )ifthechoiceinthe
first stage was ( ) while they play and other w ise. In the first
stage neith er player w ants to deviate from ( ) because the gain of
switching actions is 3 (from 2 to 5) while the loss from the punishmen t

9. Multi-Stage Games 169
in the second stage is 4 (and it is not discoun ted so it’s value remains
4). ¥
(c) What is the lo west value of for which the subgame perfect equilibriu m
y ou found in (b) survives?
Answ er: The discounted punishment m ust be at least as high as the
gain from deviation, so the inequalit y is 3 − 4 ≤ 0,andthesolutionis
≥
3
4
¥
(d) Can you find an subgame perfect equilibrium of this game whe re the
players pla y something other than ( ) or ( ) in the first stage?
Answ er: The same logic as that for parts b. and c. follows to support
the pairs of actions ( ) and () in the first stage. In eac h of these
profiles one pla yer will gain 3 by devia ting to his preferred choice, and
the loss in the second stage with properly defined contingen t strategies
is 4, so if ≥
3
4
the punishmen t will suffice to support the desired first
stage behavior. ¥
4. On lin e Gam in g: Consider a two-stage game between t wo firm s that produce
online games. In the first stage, they play a Cournot competition game (eac h
chooses a quantity
) with demand function =100−, and zero marginal
production costs (
(
)=0for =1 2) In the second stage, after observin g
the pa ir (
1
2
) and after profits have been distributed , th e p layers play a
simultaneou s move “access” gam e where they can either keep their game
platforms closed, or eac h can open it’s platform to allo w players on the other
platform to play online with pla yers on their o wn platform ( for pla yer
1, for pla yer 2), or choose to keep their platforms non-compatible ( for
player 1, for player 2), in wh ich case each platform ’s pla yers can on ly pla y
with others on their platform. If they choose ( ) then second stage pa yoffs
are (0 0). If only one firm chooses to open its platform, it bears a cost of
(−10) with no benefit since the other firm d id not allow to open access.
Finally, if both firms choose ( ) then eac h firm gets many more ey eballs

170 9. Multi-Stage Games
for advertising, and pay offsforeachfirm are 2 500.Bothplayersusethe
same discount factor to discount future payoffs.
(a) Find the unique Nash equilibrium in the firststageCournotGameand
all of the pure strategy Nash equilibria of the second stage access game.
Find all the pure strategy subgam e perfect equilibria with extreme dis-
counting ( =0). Be precise in defining history contingent strategies for
both pla yers.
Answ er: The maximization problem in the Cournot game is
max
(
)=(100−
−
)
and the first order condition is 100 −
− 2
=0resulting in the best
response function
=
100−
2
, which in turn implies that the unique
Nash equilibrium is
1
=
2
=33
1
3
. The second stage game is giv en by
the follo wing matr ix:
Player 1
Player 2
250 250 −10 0
0 −10 0 0
and it is easy to see that both ( ) and () are Nash equilibria.
Oneofthesetwowillhavetobeplayedinthesecondstageofthegame
in any subg am e perfect equilibrium. When =0the only first stage
play that is possible in eq uilibr ium is the unique Courno t equilibrium.
Therefor e, only t wo outcom es can result from a subgam e perfect equi-
librium: choose
1
=
2
=33
1
3
in the first stage and choose either ( )
or ( ) in the second stage.
1
1
There are infinitely many strategy profiles that will supp ort this outcome and by a subgame p erfect equilib-
rium. For exam p le, h ave th e players each cho ose
=33
1
3
in the first stage followed by the following contingent
strategy for the second stage: if both
1
and
2
are b elow
∗
then choose “open” ( and ) w h ile if eith e r
1
or
2
are ab ove
∗
then choose “not-o p en” ( and ). Notic e th a t th is is a n e q u ilib r iu m for a ny val ue o f
∗
.If
∗
33
1
3
the n t he sec o n d sta g e e q u ilibrium will be ( ) while if
∗
≥ 33
1
3
the n it will be ( ).

9. Multi-Stage Games 171
(b) No w let =1. Fin d a subgam e perfect equilibrium for th e two-stag e
game in which the play ers c hoose the monopoly (total profitmaximiz-
ing) quantities and split them equally (a symm e tr ic equilib rium).
Answ er: Monopoly profits in the first stage are giv en b y maximiz-
ing (100 − ) wh ich yields =50, and an equal split means that
1
=
2
=25with each firm making (100 − 50)25 = 1250 in the first
stage. Ho wever, eac h firm is tem pted to deviate given that
=25.
Using the best response deriv ed in part a. we know that the best
deviation is
0
=
100−
2
=
100−25
2
=375 and the deviator’s profits
would be (100 − 625)375 = 14063. Hence, the gain from deviating is
14063 − 1250 = 1563. Given the t wo equilibria in the second stage
game we can prevent the pla yers from deviating by introducing the fol-
lo w ing cont ingent strategies: each pla yer will play “open” if both play ed
=33
1
3
in the first stage and th ey will play “n ot open” if any other
c ho ices were made. With =1the losses from the punishment out weigh
the gains from deviation and hence it is a subgame perfect equilibrium.
¥
(c) What is the lo west value of for which the subgame perfect equilibriu m
y ou found in (b) survives?
Answ er: Itmustbethecasethatthelossfromdeviationisatleastas
painful as the gain, that is, 1563 − 250 ≤ 0,or, ≥ 06252 ¥
(d) No w let =04. Can you support a subgame perfect equilibrium for the
t wo-stage game in which the play ers choose the monopoly quantities and
split them equally? If not, w hat are the h ighest profits that th e firm s
can make in a symm etric equilibrium?
Answ er: From the analysis in part c. we know that for 06252
w e cannot support the split of monopoly profits as a subgame perfect
equilibr ium. Finding the highest profits that can be supported is a bit
tric ky. The easy part is starting with the discounted punishment value
when =04,whichis04×250 = 100. Next w e need to find a symme tric
pair (
1
2
)=(
∗
∗
) for whic h the extra profits from deviating to the

172 9. Multi-Stage Games
best response to
∗
given that the other firm sticks to
∗
is exactly equal
to 100. First, the profits from sticking to
∗
will be
∗
=(100− 2
∗
)
∗
.
Next, the best response to
∗
is
0
=
100−
∗
2
and the profits from this
deviation are
0
=(100−
∗
−
100−
∗
2
)
100−
∗
2
,andtherefore
∗
must solve
0
−
∗
=100,or
(100 −
∗
−
100 −
∗
2
)
100 −
∗
2
− (100 − 2
∗
)
∗
=100
which yields the solution
∗
=26
2
3
. Hence, for =04 the best symmet-
ric equilibrium has both players earning (100 − 2(26
2
3
))26
2
3
=1244
4
9
in
the first period followed by 250 in the second. ¥
5. Campaign Spending: Two political candidates are destined to play the
follo w ing t wo stage game. Assume throughout that there is no discounting
( =1). First, they compete in the primaries of their part y. Eac h candidate
can spend
≥ 0 reso urces on adds that reach out to voters, whic h in
turn increases the probability that candidate wins the race. Giv en a pair
of spending choices (
1
2
), the probabilit y that candidate wins is given by
1
+
2
. If neither spends any resources then eac h wins with probability
1
2
.Each
candidate values winning at a pa y off of 16 0, and the cost of spending
is
equal to
. After eac h player observes the resources spen t by the other, and
a winner in the primaries is selected, they can choose how to in teract. Each
can choose to be pleasant ( forplayer1and forplayer2)ornasty( and
respectively). A t this stage, both pla yers prefer that they be nice to each
other rather than nast y, but if a pla yer is nast y then the other prefers to be
nasty too. The pa y offs from this stage are given by the matrix where 0:
Play er 1
Play er 2
−1 0
0 −1 0 0
(a) Find the unique Nash equilibrium of the first stage game and the t wo
pure strategy Nash equilibria of the second stage game.

9. Multi-Stage Games 173
Answ er: In the first stage player maximizes
(
)=
+
16 −
and the first order condition is
16
(
+
)
2
− 1=0
which is of course symmetric for both pla yers and rep resents the best
response correspondence. Solving the tw o F OCs simultaneously yields
1
=
2
=4as the unique N ash equilibrium of the first stage game and
each candidate wins with probab ility
1
2
. The two pure strategy Nash
equilibria of the second stage game are ( ) and (). ¥
(b) What are the P areto optim al outcomes of eac h stage game?
Answ er: In the first stage th e symmetric Pareto optimal outcome is
for both to choose
1
=
2
=0. This way they win with probability
1
2
each without w asting an y resources.
2
It is easy to see that the Pa reto
optim al outcome of the second stage is ( ). ¥
(c) For whic h value of can the players support the path of Pareto optimal
outcomes as a subgam e perfect equilibrium?
Answ er: Because there is no discounting ( =1)thenthevalueof
thethreatofcontingentpunishmentinthesecondstageis for each
player because the conditional strategies will be “we pla y ( ) if we
did the righ t thing in stage 1 and otherwise we pla y ( ).” If we wish
to support the Pa reto optimal action of
1
=
2
=0in the first stage
w e need to see what the deviation payoff is. A pla yer who deviates to
an infinitesimal value
0 will win for sure and get 16 −
instead of
2
Strictly sp eaking, there is no other Pareto optimal outcome because of the continuous action spaces. If player
chooses
=0then if player chooses
= 0 then this is b etter for player than choosing
=0, bu t it is
not Pareto optimal b ecause if instead player chooses
=
2
then he is better off without making player 1 worse
off. T his is a technicality in the sense that the “Pareto frontier” includes the p oint (
1
2
)=(0 0) but any other
pair of feas ib le s tr a te g ie s is Pa ret o do m i n a te d for a t le as t o n e player.

174 9. Multi-Stage Games
getting
1
2
×16−0=8, so that the gains from deviating are infinites im ally
close to 8. Hence, if =8then no player will wish to deviate from the
proposed path of play. ¥
(d) Assume that =1. What is the “best” symmetric subgame perfect
equilibrium that the players can support?
Answ er: Themostseverethreatisthattheplayerslose =1so the
gainfromdeviatingcannotbemorethan1.Wearethereforelooking
for a symmetr ic ch oice in the fist stage,
1
=
2
=
∗
such that if some
player deviates to the best response to
=
∗
thenhisgaininthefirst
period is an expected payoff of 1. First note that if both play e rs choose
∗
then eac h gets a payoff in the first stage of 8 −
∗
because they win
with equal probabilit y. Now consider the first order condition derived in
part a. abov e. From it we can derive the best response function of each
player to be
(
)=4
√
−
. This implies that the best response to
=
∗
is
(
∗
)=4
√
∗
−
∗
, and if this is what player deviates to
then his expected payoff in the first stage gam e is
(
(
∗
)
∗
)=
4
√
∗
−
∗
4
√
∗
−
∗
+
∗
16 − (4
√
∗
−
∗
)
=16− 8
√
∗
+
∗
The best symmetric equilibrium will be ach ieved when the gains from
deviating are exactly equal to 1, or
16 − 8
√
∗
+
∗
− (8 −
∗
)=1,
which results in
∗
=
9
2
− 2
√
2 ≈ 16716. ¥
(e) What happens to the best symmetric subgame perfect equilibrium that
the players can support as c han ges? In what way is this related to
theroleplayedbyadiscountfactor?
Answ er: If increases then w e can have a harsher punishment, and
this can allo w us to deter more attractive deviations that will happen
when we try to implemen t a smaller v alue of
∗
in th e first stage. As
9. Multi-Stage Games 175
increases to wards 8 w e can get closer and closer to the Pareto optimal
outcome of
∗
=0. This carries the same intuition as a higher discount
factor, whic h mak es the punishment more sev ere for deviations in the
first stage. ¥
6. Augmented Competition: Consider two firmsplayingatwostagegame
with discoun t factor .Inthefirst stage they pla y a Cournot quan tity setting
game where eac h firm has costs
(
)=10
for ∈ {1 2} and the demand
is given by ()=100− where =
1
+
2
. In the second stage, after
the results of the Cournot game are observ ed , the firms play the follow in g
standard setting game:
Player 1
Player 2
100 100 0 0
0 0 300 300
(a) Find the unique Nash equilibrium of the first stage game and the t wo
pure strategy Nash equilibria of the second stage game.
Answ er: In the first stage game each player maximizes (100 −
−
)
− 10
which yields the best response function
=
90−
2
and the
unique Nash equilibrium is
=
=30. The two pure strategy Nash
equilibria in the second stage are ( ) and ( ). ¥
(b) As far as the t wo firm s are considered, what are the symm etric P areto
optimal outcomes of eac h stage game?
Answ er: In the first stage game it is splitting the monopoly profits and
in the second stage it is ( ) because 300 100. M onopoly profits in
the first stage are earned when w e maximize (100 −
−
)(
+
) −
10(
+
) which is obtained when
+
=45. Hence, the symmetric
Pareto optimal outcome is
1
=
2
=225 in the first stage, whic h yields
apayoff of 10125 for each pla yer, and ( ) in the second, whic h yields
apayoff of 300 for eac h pla yer. ¥

176 9. Multi-Stage Games
(c) For wh ich values of can the Pa reto optimal outcomes be supported as
a subgame perfect equilibrium?
Answ er: In the P areto optimal outcome of the first stage each firm
earns a profitof is tempted to deviate giv en that
=225.Using
the best response derived in part a. we kn ow that the best deviation
is
0
=
90−
2
=
90−225
2
=3375 and the deviator’s profits w ould be
(100−225−3375)3375−10(3375) = 11390625. Hence, the gain from
deviating is 11390625 −10125=1265625. Given the t wo equilibria in
the second stage game w e can try and prev ent the players from deviating
by using contingent strategies: each player will pla y (or )ifboth
played
=225 in th e first stage and they w ill pla y (or )ifany
other choices w ere made. This will cause the deviating pla y er a loss of
200 in the second stage, and for this to deter the best deviation in the
first stage it must be th at 1265625 − 200 ≤ 0,andthesolutionis
≥ 063281. ¥
(d) Assume that =05. W hat is the “best” sy m m etric subgam e perfect
equilibrium that the players can support?
Answ er: Finding the highest profits (“best”) that can be supported as a
subgam e perfect equilibrium is a bit tricky. The easy part is starting with
the discounted punishment value when =05,whichis05×200 = 100.
Next we need to find a symm etric pair (
1
2
)=(
∗
∗
) for w hic h
the extra profits from deviating to the best response to
∗
given that
the other firm sticks to
∗
is exactly equal to 100. First, the p rofits
from stick ing to
∗
will be
∗
=(100− 2
∗
)
∗
− 10
∗
. Next, the best
response to
∗
is
0
=
90−
∗
2
and the profits from this deviation are
0
=(100−
∗
−
90−
∗
2
)
90−
∗
2
− 10(
90−
∗
2
), and therefor e
∗
must solve
0
−
∗
=100,or
(100−
∗
−
90 −
∗
2
)
90 −
∗
2
−10
µ
90 −
∗
2
¶
−[(100−2
∗
)
∗
−10
∗
]=100

9. Multi-Stage Games 177
and the solution is
∗
=23
1
3
.Hence,for =05 the best symm etric
equilibr iu m has each pla yer earning (100−2(23
1
3
))23
1
3
−10(23
1
3
) = 1011
1
9
in the first stage follo wed by 300 in the second. ¥
(e) What happens to the best symmetric subgame perfect equilibrium that
the players can support as drops towards zero?
Answ er: As d rop s towards zero the ability to punish becom es less
effective and the best subgam e perfect equilibrium quan tities in the first
stage will grow un til they reach the Nash (Co urn ot) equilibrium of the
first stage,
1
=
2
=30. ¥
178 9. Multi-Stage Games
This is page 179
Printer: Opaque
t
10
Repeated Games
1. Medicare Drug Policy: In early 2005 there w a s a discussion of a proposed
policy of the US federal administratio n that supported the use of so called
“discount cards” that pharm aceutical firm s can offer senior citizens for the
purchase of medication s. These cards will have a subscription fee, and they
will in return offer discounts if prescription drugs are bought through the
issuing companies. The federal administration argued that any of the large
pharmaceutical companies can enter this market for discoun t cards, which in
turn will promote competition. To ensure this the governmen t has a website
with posted prices and posted discounts that go with eac h card. Som e con-
sume r adv ocates suggest that the compan ies will just hike up prices and offer
a discount over this higher prices, resulting in less welfa re for consumers. The
administra tion argued that this does not make too m uch sense because there
is entry and competition. Can y ou argue, usin g some formal id eas on tacit
collusion, that the way things are set up it is in fact possible, and maybe even
easier, for the firmstosqueezemoreprofits at the expense of consumers?
Answ er: By having a central place in whic h prices are posted the govern-
ment mak es it easy for companies to monitor eac h other’s prices, and this in
turnmakesiteasiertosustaintacitcollusionbecauseitcompanieswhodevi-
180 10. Repeated Games
ate from the tacit agreement will be easily detected b y the other companies.
¥
2. Grim Trigger: Consider the infin itely repeated game with discoun t factor
1 of the following variant of the Prisoner ’s dilemma:
player 1
Play er 2
6 6 −1 7 −2 8
7 −1 4 4 −1 5
8 −2 5 −1 0 0
(a) For which values of the discoun t factor can the play ers support the
pair of actions ( )playedineveryperiod?
Answ er: The grim trigger strategy is to revert to pla ying ( ) forever
yielding a discoun ted sum of payoffs(andanaveragepayoff) equal to 0.
The discounted sum of pa yoffsfromstickingtothepair( ) forever is
4
1−
. A player who deviates gets 5 instead of 4 in the period of deviation,
but then gets 0 thereafter. Hence a deviatio n will not be profitable if
4
1−
≥ 5,or ≥
1
5
¥
(b) For whic h values of the discoun t factor can the pla yers support the pair
of actions () played in ev ery period? Why is y our answer differen t
from part (a) above?
Answ er: The discoun ted sum of payoffsfromstickingtothepair()
fore ver is
6
1−
. A player who deviates gets 8 instead of 6 in the period
of deviation, but then gets 0 thereafter using grim trigger. Hence a
deviation will not be profitable if
6
1−
≥ 8,or ≥
1
4
¥

10. Repeated Games 181
3. Not so Grim Trigger:Considertheinfinitely repeated Prisoner’s Dilemma
with discount factor 1 described b y the follow ing m atrix:
Player 1
Player 2
4 4 −1 5
5 −1 1 1
Instead of using “grim trigger” strategies to support a pair of actions (
1
2
)
other than ( ) as a subgame perfect equilibriu m , assum e that the player
wish to c hoose a less draconian punishm ent called a “length punishment”
strategy. Nam ely, if there is a deviation from (
1
2
) then the play ers will pla y
( )for periods,andthenresumeplaying(
1
2
). Let
be the critical
discount factor so that if
then the adequately defined strategies will
implem ent the desired path of play with length punishment as the threat.
(a) Let =1. What is the critical value
1
to support the pair of actions
() played in every period?
Answ er: T he proposed one period punishment mean s that instead of
getting 4 for the period after deviation, the players will get 1, and after-
wards will resort to getting 4 forev er. Hen ce, the punishment is of size
3 and the discounted value is 3. The gain from deviating in one period
is getting 5 instead of 4 so this will be deterred if 1 ≤ 3 or ≥
1
3
.
1
¥
(b) Let =2. Wha t is the critical value
to support the pair of actions
() played in every period?
2
Answ er: The proposed two period punishmen t means that instead of
getting 4 for the two periods after deviation, the players will get 1,
1
To see this using the w hole stream of payoffs, sticking to ( ) yields
4
1−
while dev iating w ith th e th reat
of a one p eriod punishment will yield 5+1+
2
4
1−
andthisisnotprofitable if
4
1−
≥ 5+1+
2
4
1−
,which
can b e rewritten as 4+4+
2
4
1−
≥ 5+1+
2
4
1−
whichinturnreducesto3 ≥ 1.
2
Helpful hint: You should encounter an equation of the form
3
− ( +1) +1=0 fo r which it is e a sy to s ee
that =1is a roo t. In this case, you kn ow that th e equ ation can be w ritten in the form ( − 1)(
2
+ − 1) = 0
and solve for the other relevant ro ot of the cubic equation.

182 10. Repeated Games
and afterwards will resort to getting 4 forev er. H ence, the discoun ted
punishment is ( +
2
)3. The gain from deviating in one period is getting
5insteadof4sothiswillbedeterredif1 ≤ (+
2
)3,or ≥
1
6
√
3
√
7−
1
2
≈
026376.
3
¥
(c) Compare the tw o critical values in parts (a) and (b) abo v e. Ho w do they
differ and what is the intuition for this?
Answ er: Thepunishmentinpartb. last for two periods which is more
severe than the one period pun ishm ent in part a. This means that it
can be supported with a lower discoun t factor because the in tensity of
the punishment is increasing either in the length or when we ha ve less
discounting. ¥
4. Trust off-th e-e q u ilib riu m-path : Recall the trust game depicted in Figure
10.1. We argued that for ≥
1
2
the follow ing pair of strategies is a subgame
perfect equilibrium . For pla yer 1: “in period 1 I will trust player 2, and as as
long as there w ere no deviation s from the pair () in any period, then I
will continue to trust him. Once such a deviation occurs then I will not trust
him forever after.” For player 2: “in period 1 I will cooperate, and as as long
as there w ere no deviations from the pair () in any period, then I w ill
con tinue to do so. O n ce such a d eviation occurs then I w ill deviate forever
after.” Show that if instead pla yer 2 uses the strategy “as long as pla yer 1
trusts me I will cooperate” then the path () pla yed forever is a Nash
equilibrium for ≥
1
2
but is not a subgam e perfect equilibriu m for any value
of .
Answ er: It is easy to see th at this is a Nash equilibrium: th e equilibrium
path is followed because neither player benefits from deviating as they both
believe that a deviation will call for the continuation of grim trigger. To
see that it is not subgame perfect consider the subg am e that follow s after
3
To see this using the whole stream of payoffs, sticking to ( ) yields
4
1−
wh ile d e viatin g with t h e t h re a t o f
a two p erio d punishm ent w ill yield 5+1+
2
1+
3
4
1−
and this is not profitable if
4
1−
≥ 5+1+
2
1+
3
4
1−
.
This can either b e solved as a cubic inequality or can b e rewritten as 4+4+
2
4+
3
4
1−
≥ 5+1+
2
1+
3
4
1−
whichinturnreducesto( +
2
)3 ≥ 1.

10. Repeated Games 183
a deviation of pla yer 2 from to . The strategy of pla yer 1 is to not
trust forever which will revert the payoff to 0 in ev ery period, but pla yer 2’s
strategy is to cooperate as long as player 1 tru sts. So, after a deviation by
player 2, if player 1 believes that pla yer 2 will inde ed cooperate then player
1 should con tinue to trust. ¥
5. Negativ e Ad Cam p aigns (revisited): Reca ll the exer cise from cha pter
?? in whic h eac h one of two political parties can choose to b uy time on
commercial radio shows to broadcast negative ad campaigns against their
rival.Thesechoicesaremadesimultaneously.Duetogovernmentregulation
it is forbidden to buy more than 2 hours of negativ e campaign time so that
eac h party cannot choose an amount of negative campaigning above 2 hours.
Given a pair of choices (
1
2
),thepayoff of part y is given b y the follo w in g
function:
(
1
2
)=
− 2
+
− (
)
2
(a) Find the uniqu e pure strategy Nash equilibrium of the one shot game.
Answ er: Eac h player maximizes
(
1
2
)=
− 2
+
− (
)
2
resulting in the first order optimality condition 1+
−2
=0, yieldin g
the best response function,
(
)=
1+
2
Solving the two best response functions sim u ltaneously,
1
=
1+
2
2
and
2
=
1+
1
2
yields the Nash equilibrium
1
=
2
=1, and this is the unique solution
to these equations implying that this is the unique equilibrium. Each
player obtains a payoff of −1. ¥
(b) If the parties could sign a binding agreement on how much to campaign ,
what levels would they c hoose?
Answ er: They would choose
1
=
2
=0and each would obtain a
pa y off of 0. ¥

184 10. Repeated Games
(c) No w assume that this gam e is repeated infinitely often, and the abo ve
demonstrates the choices and pa yoffs per period. For which discount fac-
tors ∈ (0 1) can the levels you found in part (b) above be supported
as a subg ame perfect equilibrium of the infinitely repeated game?
Answ er: Consider the grim trigger strategy where the pla yers will re-
v e rt to playing the one-shot Nash forever after a deviation. The temp -
tation to deviate from 0 is the v alue a play er gains when he chooses the
best response to 0, which is
=
1
2
, whic h yields the one shot pay off of
1
4
.
Hence, the deviation will not be profitable if
1
4
−
1
1−
≤ 0,or ∈ [
1
5
1).
(d) Despite the parties ab ility to coordinate as you have demon strated in
y o ur answer to (c) abo ve, the government is concerned about the parties
ability to place up to 2 hours a day of negative cam p aign in g, and it is
consid erin g lim itin g negative campa ign ing to
1
2
hour a day so that now
∈ [0
1
2
] Is this a good policy to further limit negative campaign s?
Justify your answer with the relevant calculation s. Wha t is the intu ition
foryourconclusion?
Answ er: If this were just a one shot game then the government’s regu-
lation wo uld be beneficial. Instead of c h oosing
1
=
2
=1they w ould
choose
1
=
2
=
1
2
and receive −
1
2
each in stea d of −1. Howev er, for
the repeated game this regulation makes the grim trigger threat less
severe, and cooperation on spending nothing can only be ac h ieved if
1
4
−
05
1−
≤ 0,whichholdsfor ∈ [
1
3
1). Hence, for ∈ [
1
5
1
3
) the play-
ers will no longer be able to achieve the P ar eto optimal outcome using
repeated game cooperation, making this regulation a bad idea. ¥
6. Regulating Medications: Consider a firm(player1)thatproducesaunique
kind of drug that is used by a consumer (pla yer 2). This drug is regulated b y
the go vernmen t so that the price of the drug is =6.Thispriceisfixed, but
the quality of the drug depends on the man ufacturing procedure. The “good”
() manufacturing procedure costs 4 to the firm , and yields a value of 7 to

10. Repeated Games 185
FIGURE 10.1.
theconsumer.The“bad”() man ufactur ing procedure costs 0 to the firm,
and yields a valu e of 4 to the consumer. The consumer can ch oose whether
to buy or not at the price , and this decision mu st be made before the ac-
tual manufa cturing procedure is revea led. However, after consumptio n, the
true qualit y is revealed to the consumer. The ch oice of m anufacturing pro-
cedure,andthecostofproduction,ismadebeforethefirm kno w s whether
theconsumerwillbuyornot.
(a) Dra w the game tree and the matrix of this game , and find all the Nash
equilib ria of this game.
Answ er: Let play er 1 be the firm who can c hoose (good) or (bad),
and player 2 is th e consumer who can choose (purc hase) or (not
purc hase). If, for example, the pla yers choose ( ) then the firm gets
6−4=2and the consumer gets 7−6=1. In a similar way the complete
matrix of this one shot game can be represen ted as follo w s:
Play er 1
Play er 2
2 1 −4 0
6 −2 0 0
The extensiv e form game tree is,¥
(b) No w assum e that the game described abo ve is repeated t w ice. (The con-
sumer learns the qualit y of the p roduct in each period only if he con-

186 10. Repeated Games
sumes.) Assume that each pla yer tries to maxim ize the (non-discoun ted )
sum of his stage pa yoffs. Find all the subg ame-perfect equilibr ia of this
game.
Answ er: Itiseasytoseethatplayer1hasadominantstrategyinthe
stage game: c hoose , and pla yer 2’s best response is to choose .This
unique N ash equ ilibriu m m ust be pla yed in the seco nd sta ge, and by
backward induction must also be pla yed in the first stag e. hence, it is
theuniquesubgameperfectequilibrium.
(c) No w assume that the gam e as repeated infin itely ma ny tim es. Assume
that eac h pla y er tries to maximize the discounted sum of his or her
stage payoffs, where the discoun t rate is ∈ (0 1). What is the range
of discount factors for whic h the good m anufa cturing procedure will be
used as part of a subgame perfect equilibrium?
Answ er: Consider the grim trigger strategies: pla yer 1 c hooses and
contin ues to choose as long as he chose in the past and as long
as play er 2 purc hased . O therwise he chooses forever after. P layer 2
c h ooses and contin ues to c hoose as long as he chose and play er 1
chose . Otherwise he pla ys forever after. Player 2 has no incentive
to deviate at any stage, but player 1 can gain 4 from switc h ing to in
any period (get 6 instead of 2). He will no t have an incentive to deviate
if 4 ≤
2
1−
, whic h holds for ∈ [
1
2
1) ¥
(d) Consume r adv ocates are pushing for a lo wer price o f the drug, say 5.
The firm wants to approach the Federal trade Commission and argue
that if the regulated price is decreased to 5 then this may have dire
consequences for both consumers and the firm . Can you make a formal
argumen t using the parameters abo v e to support the firm? What about
the consumers?
Answ er: If the price of the drug is lowered to 5 then p layer 1 has a
stronger relative temptation to deviate from the grim trigger strategies
described in par t c. above. His gain from deviation is still 4, but the
gain from continuing to ch oose is only 1 per period and not 2. Hence,

10. Repeated Games 187
hewillnothaveanincentivetodeviateif4 ≤
1
1−
,whichholdsfor
∈ [
3
4
1). Hence, if the firm can argue that ∈ [
1
2
3
4
) then increasing
the price from 4 to 5 w ill ca use the good equilibrium to colla ps e and
no trade will occur. The argument in favor of raising the price can be
made if ∈ [
3
4
1) because then the consumers benefitattheexpenseof
the firm but there is enough surplus to support the good outcome. ¥
7. Diluted Happiness: Consider a relationship betw een a bartender and a
customer. The bartender serves bourbon to the customer, and c hooses ∈
[0 1] whic h is the proportion of bourbon in the drink serv ed, while 1 −
is the p roportion of water. T h e cost of su pply ing such a drink (standa rd 4
once glass) is where 0. The C u stom er , w ithou t kn owin g , decides
on wheth er or not to bu y the drink at the m ar ket price .Ifhebuysthe
drink, his pay off is − and the bartender’s payoff is −. Assum e that
,andallpayoffs are common knowledge. If the customer does not buy
thedrink,hegets0,andthebartendergets−(). because the customer
hassomeexperience,oncethedrinkisboughtandhetastesit,helearnsthe
value of , but this is only after he pays for the drink.
(a) Find all the Nash equilib r ia of this game.
Answ er: The customer has to buy the drink without knowing its con-
tent, implying that the bartender has a dominant strategy which is to
choose =0once the customer p ays for the drink. Bu t anticipating
that, the customer would not buy the drink. Hence, the unique N ash
equilibrium is for the custom er not to buy and the bartender to c h oose
=0if he does buy. ¥
(b) No w assume that the custom er is visiting town for 10 days, and this “bar
game” will be pla yed for eac h of the 10 evenings that the customer is in
to w n . A ssum e that eac h player tries to maxim ize the (non-discounted)
sum of his stage payoffs. Find all subgame -perfect equilibria of this
game.
Answ er: The game just unravels: in the last period they m ust play

188 10. Repeated Games
theuniqueNashinparta. above. But then they will do the same in
the pen ultimate period, and so in un til the beginning of the game. The
unique subgame perfect equilibrium is therefore for the customer not to
buy in an y of the 10 periods and for the bartender to choose =0in a
period where the customer buys. ¥
(c) No w assume that the customer is a local, and the players perceive the
game as repeated infinitely many times. Assume that each player tries
to maxim ize the discounted sum of his or her stage payoffs, where dis-
countrateis ∈ (0 1). What is the range of prices (expressed in the
param eters of the problem) for which there exists a subgame-perfect
equilibrium in which everyday the bartender chooses =1and the
customer buys at the price ?
Answ er: For a transaction to occur both hav e to get a non-negativ e
pa y off, implying first that ∈ [ ]. We will consider a subgame perfect
equilibrium with grim trigger strategies that reverts to no-pur chase if
anyone ev er deviates. Notice that the customer has no incentive to ever
deviate if ≤ because he gains nothing or loses some positive value
from not buying. The bartender does benefit in the one shot game from
deviating to =0and obtaining instead of −. Given some value of
, the bartender will not deviate if ≤
−
1−
,or ≥
(which is of course
greater than ). Hence, if
≤ then for any price ∈ [
] there exists
a subgam e perfect equilibrium in which every day the bartender chooses
=1and the customer buys at the price .If,however,
then no
suc h price exists. ¥
(d) For which values of (expressed in the parameters of the problem) can
suc h a price range that you found in (5) above exist?
Answ er: Th e condition for such a subgame perfect equilibrium is that
≤ wh ich implies that must satisfy ≥
. ¥

10. Repeated Games 189
8. Tacit C o llu sion : There are t w o firmsthathavezeromarginalcostandno
fixed cost that produce some good, each producing
≥ 0∈ {1 2}.The
demand for this good is giv en by = 200 − ,where =
1
+
2
.
(a) First consider the case of Cournot competition, where each firm chooses
, and that this game is infinitely repeated with a discount factor 1.
Solve for the static stage-game Cournot-N a sh equilib riu m .
Answ er: Each firm solves max
(200 −
−
)
so the first order
condition is 200 −2
−
=0and the best response is
=
200−
2
.The
uniqu e N as h equilibrium is therefore
1
=
2
=66
2
3
. The profits of each
firm would be 4 444
4
9
. ¥
(b) For which values of can y ou su pport the firm s equally splitting
monopoly profits in eac h period as a subgam e perfect equilibriu m that
uses “trigger stra tegies”? (i.e., after one deviates from the proposed
split, they resort to the static Cournot-Na sh equilibrium thereafter).
Note: be careful in defining the strategies of the firm s.
Answ er: The monopoly profits is obtained from maxim izin g (200−)
which occurs at =100with combined profits being 10 000 or
=50
and profits are 5 000 for each firm. If firm is producing 50, however,
then the best deviation for firm is giv en by the best response,
=
200−50
2
=75,andfirm ’s profits in the period when it deviates are
(200−75 −50)75 = 5 625. Consider trigger strategies of the form “start
by choosing
=50andcontinuetochoosesoaslongasbothfirms
follow this path, yet if an y firm ever deviates form this path rev ert to
=66
2
3
forever after.” The devia tio n will not be wor thw h ile if
5625 +
1 −
(4444
4
9
) ≤
5000
1 −
which holds if ∈ [
9
17
1). ¥
(c) No w assume that the firms compete à la Bertrand , each c hoosing a price
≥ 0, where the lowest priced firm gets all the demand, and in case of a
190 10. Repeated Games
tie they split the market. Solv e for the static stage-game Bertrand-N ash
equilib r iu m .
Answ er: The static Bertrand -N ash equilibrium is for each form to
choose
=0because they hav e zero mar ginal costs. Profits will be
zero for each firm. ¥
(d) For which values of can you support the firm s splitting m ono poly
profits in each period as a subgam e perfect equilibrium that uses “trigger
strategies”? (i.e., after one deviates from the proposed split, they resort
to the static Ber tran d—N ash equilibrium thereafter). Note: be careful in
defining the strategies of the firms!
Answ er: The monopoly profits are o btained from choosing
=100
with combined profits being 10 000 and profits are 5 000 for each firm if
they split production equally. If firm is charges 100, however, then firm
can deviate to some price
=100− for infinitesimally small and
firm ’s profits in the period when it deviates will be infinitesim ally close
to 10 000. Consider trigger strategies of th e form “start b y choosing
=100andcontinuetochoosesoaslongasbothfirms follow th is
path, yet if any firm ev er deviates form this path revert to
=0
forever after.” Th e deviat ion w ill not be w o rthwhile if
10000 +
1 −
(0) ≤
5000
1 −
which holds if ∈ [
1
2
1). ¥
(e) No w instead of using trigger strategies, try to support the firms equally
splitting monopoly profits as a subgame perfect equilibrium where after
adeviation,firm s would resort to the static Bertrand competition for
only t w o periods. For which values of will this w ork ? Why is this
different than you r answer in (d) above?
Answ er: Because we are only punishing for two periods, the deviation
will not be worth w hile if
10000 + (0) +
2
(0) +
3
5000
1 −
≤
5000
1 −
10. Repeated Games 191
or
2
+ −1 ≥ 0, which results in ≥
1
2
√
5 −
1
2
≈ 0618.Thereasonwe
need a larger discount factor is that the punishment is less sev ere as it
lasts for only two periods and not infinitely man y. ¥
9. Negative Externalities: Two firm s are located adjacent to one another
and each im poses an external cost on the other: the detergen t that Firm 1
uses in it’s laundry business makes the fish that firm 2 catches in the lake
tastefunny,andthesmokethatfirm 2 uses to smoke its caugh t fish m akes
the cloth es that firm 1 hand s o ut to dry smell funny. As a consequence,
eac h firms profits are increasing it its o wn production and decreasing in the
production of its neigh boring firm. In particular, if
1
and
2
are the firms’
production levels then their per-period (stage gam e) profits are given by
1
(
1
2
)=(30−
2
)
1
−
2
1
and
2
(
1
2
)=(30−
1
)
2
−
2
2
.
(a) Dra w the firm s’ best response functions and fin d the Na sh equilibriu m
of the stage game. How does this compa re to the P ar eto optimal stage-
game profitlevels?
Answ er: Each firm maximizes
1
(
)=(30−
)
−
2
and the first
order condition is 30 −
−2
=0, resulting in the best response func-
tion
=
30−
2
as dra wn in the following figure:
0 10 20 30
0
10
20
30
q_1
q_2
The uniq ue Na sh equ ilib rium is
1
=
2
=10giving eac h firm a profit
of 100. To solve for the Pareto optimal outcome w e can maximize the
sum of profits,
max
1
2
(
1
2
)=(30−
2
)
1
−
2
1
+(30−
1
)
2
−
2
2

192 10. Repeated Games
and the two first order conditions are
(
1
2
)
1
=30−
2
− 2
1
−
2
=0
(
1
2
)
2
=30−
1
− 2
2
−
1
=0
and solving them together yields
1
=
2
=7
1
2
and the profits of each
firm are 112
1
2
. ¥
(b) For whic h levels of discount factors can the firms support the P areto
optim al lev el of quantities in an infinitely repeated game?
Answ er: We consider grim trigger strategies of the form “I will c h oose
=75 and continue to do so as long as both c hose this value. If anyone
ever deviates I w ill revert to
=10forev er.” The best deviation from
=75 giv en that
=75 is to ch oose the best response to 75 which is
30−75
2
=1125,andtheprofitfromdeviatingis(30 −7
1
2
)11
1
4
−(11
1
4
)
2
=
2025
16
=126
9
16
. Thus, each player will not w ant to deviate if
126
9
16
+
100
1 −
≤
112
1
2
1 −
which holds for ∈ [
9
17
1). ¥
10. La w Merc hants (revisited): Consider the three person game described
in section ??. A subgame perfect equilibrium was constructed with a bond
equal to 2,andawagepaidbyeveryplayer
2
to player 3 equal to =01,
anditwasshownthatitisindeedanequilibriumforanydiscountfactor
≥ 095. Show that a similar equilibrium, where players
1
trust players
2
who post bonds, play ers
2
post bonds and cooperate, and pla yer 3 follow s
the contract in every period, for any discoun t factor 0 1.
Answ er: First notice that the bond need not be equal to 2 because player
2
only gains 1 from deviating. Hence, any bond of value 1+1 will
deter play er
2
from c h oosing to defect instead of cooperate. Second , notice
that fo r any w age to the third party of 1 − 1 player
2
still get a

10. Repeated Games 193
positive surplus 0 from engaging the services of the third part y. Hen ce,
for any value of ∈ (0 1),postingabondof1+ and pa y ing the third part y
1 − guaran tees that player
2
will choose to emplo y the third party and
cooperates if trusted, and in turn,
1
will c h oose to trust. We are left to see
whether the third party prefers to return the bond as promised or if he would
deviate and give up the future stream of all income. By deviating the third
party pockets the bon wo rth 1+, and giv es up the future series of w ag es
1 − for all future periods. He nc e, he will not deviate if
1+ ≤
1 −
(2 − )
which for ∈ (0 1) holds for ∈ (
1+
2
1). Hence, for any
1
2
there exists
a small enough 0 for whic h the inequality above holds. ¥
11. Trading Brand Names: Show that the strategies proposed in Section ??
constitute a subgame perfect equilibrium of the sequence of trust gam es.
Answ er: Conside r any pla yer
2
, 1 Under the proposed strategies, if
trust was never abused and the name w as bought up till period −1 then ()
b y buying the name and cooperating he is guaran teed a payoff of 1, ()by
buying the name and defecting he receiv es 2 but cannot sell the name to the
next pla y er 2 and hence he gets 2 −
∗
1,and() b y not buying the name
he gets 0. He nce, for any the strategy of
2
is a best response. Consider
player
1
2
.Ifhe() by creating the name and cooperating he is guaranteed
apayoff of 1+
∗
2,() by not creating the name he gets 0. Hence, the
strategy of
1
2
is a best r esponse. Last, it is easy to see tha t an y pla yer 1
can expect cooperation, and hence trusting is a best response conditional on
no one ever defecting and the name being created and transmitted. ¥
12. Folk Theorem (revisited): Consider the infinitely repeated trust g am e
describedinFigure10.1.
(a) Draw the convex hull of average payoffs.
Answ er: ¥
194 10. Repeated Games
FIGURE 10.2.
(b) Are the average pa yoffs (
1
2
)=(−04 11) in the convex hull of av-
erage payoffs? Can they be supported by a pair of strategies that form
a subgame perfect equilibrium for a large enough discount factor ?
Answ er: The a v erage pa y offs (
1
2
)=(−04 11) are in the con vex
h ull of average payoffs. It is easy to see that the point (−04 08) is
on the line that connects the poin t (−1 2) with (0 0),andthepoint
(−04 17) thelinethatconnectsthepoint(−1 2) with (1 1). It follo w s
that the point (−04 11) is in the interior of the convex hull of payoffs.
How ev er, these pa yoffs cannot be supported by a subgame perfect equi-
librium because pla yer 1 is expected to get an a verage pa yoff of −04,
but he can guaran tee himself a pa yoff of 0 b y c hoosing never to trust.
¥
(c) Sho w that there is a pair of subgame perfect equilibrium strategies for
the t wo play ers that yields a v erage payoffsthatapproach(
1
2
)=
(
1
3
4
3
) as approac h es 1.
Answ er: Firstnotethatthepoint(
1
3
4
3
) thelinethatconnectsthepoint
(−1 2) with (1 1). Tha t is, it is a weighted a verage of the two points as
follow s:
1
3
(−1 2)+
2
3
(1 1) = (
1
3
4
3
). This suggests that the average payoff
wearetryingtoachieveisa
1
3
:
2
3
weighted average between the pairs
of actions () and (). So, consider the the follo w ing strategies:
10. Repeated Games 195
Player 2 will play twice and then once, and repeat this pattern
(play in =1 2 4 5 7 and pla y in =3 6 9 ). P layer 1
will pla y ever y period. If either pla yer deviates from these proposed
strategies then both players rev ert to playing ( ) forever after. The
pa y off for pla yer 1 is,
1
=(1− )(1 + +
2
(−1) +
3
+ ···)
=(1− )(
1
1 −
3
+
1 −
3
−
2
1 −
3
)
=(1− )
1+ −
2
(1 − )(1 + +
2
)
=
1+ −
2
1+ +
2
and it follo ws that
lim
→1
1+ −
2
1+ +
2
=
1
3
.
Similarly,
2
=(1− )(1 + +
2
(2) +
3
+ ···)
=(1− )(
1
1 −
3
+
1 −
3
+
2
2
1 −
3
)
=
1+ +2
2
1+ +
2
and it follo ws that
lim
→1
1+ +2
2
1+ +
2
=
4
3
.
Hence, as → 1 the average payoffs from this subgame perfect equilib-
rium conv erge to (
1
3
4
3
). ¥
196 10. Repeated Games
This is page 197
Printer: Opaque
t
11
Strategic Bargaining
1. Disagreement: Construct a pair of strategies for the ultimatum game ( =
1 bargaining gam e) that constitute a Nash equilibrium , which together sup-
port the outcome that there is no agreement reac hed b y the two players and
the payoffs are zero to each. Show that this disagreem ent outcome can be
supported b y a Nash equilibr ium regardless of the nu mber of bargain ing pe-
riods.
Answ er: Co nsider the following strategies: player 1 offers nothing to player
2( =0) and pla yer 2 only accepts if he is offered all of the surplus ( =1).
In this case both players are indifferent (pla yer 1 is indifferent between an y
offer and play e r 2 is indifferent bet ween accepting and rejecting), and both
receive zero. It is easy to see that repeating these strategies for any length of
the game will still constitute a N a sh equilibr ium. ¥
2. Hold Up: Co n side ring an ultim atu m game ( =1bargaining game) where
before pla yer 1 makes his offer to play er 2, pla yer 2 can in vest in the size of the
pie. If player 2 c hooses a low level of in vestmen t () then the size of the pie
is small, equal to
while if play e r 2 c h ooses a high level of investment ()
thenthesizeofthepieislarge,equalto
. The cost to pla yer 2 of choosing
198 11. Strategic Bargaining
is
, while the cost of ch oosing is
Assume that
0,
0 and
−
−
.
(a) What is the unique subgame perfect equilibrium of this game? Is it
Pareto Optimal?
Answ er: Solvin g this ga m e bac kward, w e kno w that the ultimatum
game has a unique equilibrium in which player 1 will offer nothing to
player 2 and pla yer 2 will accept the offer. Working backwards, if player 2
first chooses the lo w lev el of investment then his payoff will be −
, while
he will be worse off if he chooses the high lev el of investm ent because
−
−
. Hence, the unique subgam e perfect equilibrium has player
2 first choose the lo w lev el of inv estmen t, then pla yer 1 offering to keep
all the value
to him self, and fin ally player 2 accepting the offer and
getting −
. ¥
(b) Can y ou find a Nash equilibrium of the game that results in an outcome
that is better for both pla yers as compared to the unique subgame
perfect equilib riu m?
Answ er: Consider the following strategy for pla y er 2: firstchoosethe
high lev el of investment, and then accept any offer that gives himself at
least
−
− for small. Given this strategy, pla yer 1’s best response
is to offer to keep
+ for him self and
−
− for pla yer 2. Player
2’s payoff is then
−
− −
−
for small enough ,andplayer
1’s pa yoff is
+
sotheplayersarebothbetteroff. ¥
3. Ev en/Odd Symmetry: In section ?? we analyzed the alternating bargain-
ing game for a finite number of periods when w as odd. Repeat the analysis
for even.
Answ er: Consider the case with an even n umber of rounds ∞, imply in g
that player 2 has the last mo ver advan t ages. The following bac k ward induc-
tion argumen t applies:
-Inperiod , player 1 accepts any offer, so player 2 offers =0and pay o ffs

11. Strategic Bargaining 199
are
1
=0;
2
=
−1
-Inperiod −1 (odd period — pla yer 1 offers), by bac kward induction pla yer
2 should accept an ything resulting in a pay off of
2
≥
−1
. If player 2 is of-
fered in period − 1 then
2
=
−2
(1 − ); Th is imp lies that in period
−1 player 2 will accept an y (1 −) ≥ and by bac kward induction player
1shouldoffer =1− , whic h yields play er 1 a pa yoff of
1
=(1− )
−2
and
2
=
−1
-Inperiod −2 (ev en period), conditional on the analysis for −1,player1’s
best response is to accept an y that giv es him
−3
≥ (1 − )
−2
Pla yer
2’s best response to this is to offer the smallest that satisfies this inequa l-
it y, and solving it with equalit y yields play er 2’s best response: = −
2
This offer follo wed by 1’s acceptance yields
1
=
−3
=
−2
−
−1
and
2
=
−3
(1 − )=
−3
−
−2
+
−1
.
We can con tinue with this tedious exercise only to realize that a simple pat-
tern emerges. If w e consider the solution for an ev en period − ( being
ev en because is assumed to be ev en) then the bac kward induction argume nt
leads to the sequentially rational offer,
−
= −
2
+
3
···−
while for a n odd period − ( being odd) then the bac kward induction
argument leads to the sequentia lly rationa l offer ,
−
=1− +
2
···−
.
We can use this Pattern to solve for the subgame perfect equilibr ium offer in
the first period,
1
whic h b y bac kward induction m ust be accepted by player
2, and it is equal to
1
=1− +
2
−
3
+
4
···−
−1
=
=(1+
2
+
4
+ ···+
−2
) − ( +
3
+
5
+ ···+
−1
)
=
1 −
1 −
2
−
−
+1
1 −
2
=
1 −
1+

200 11. Strategic Bargaining
andthisinturnimpliesthat
∗
1
=
1
=
1 −
1+
and
∗
2
=(1−
1
)=
+
1+
¥
4. Con stant Delay Cost: Consider a two player alternating bargaining gam e
where instead of the pie shrink ing by a discount factor 1, the pla yers
eac h pa y a cost
0, ∈ {1 2} to advance from one period to another. So,
if player receiv es a share of the pie that gives him a value of
in period
then his pa yoff is
=
− ( − 1)
. If the game has periods then a
sequence of rejections results in each player receiving
= −( − 1)
.
(a) Assume that =2. Find the subgame perfect equilibrium of the game
and sho w in whic h w ay it depends on the values of
1
and
2
.
Answ er: Inthelastperiodplayer2makestheoffer in an ultimatum
game and will offer to k eep the whole pie:
1
=0and
2
=1 and
player 1 is will accep t (he’s indifferen t). P ayoffswouldbe
1
= −
1
and
2
=1−
2
.Goingbackwardstoperiod1,player1hastooffer at
least
2
=1−
2
to player 2 for him to accept, so the unique subgame
perfect equ ilibriu m has pla yer 1 offering 1 −
2
to pla yer 2, and player
2 accepts a nticipating that he will offer and get
2
=1in the second
period follow ing rejection. Pa yoffsare
1
=
2
and
2
=1−
2
.Payoffs
therefore do not depend on
1
. ¥
(b) Are there Nash equilibria in the t wo period game that are not subgame
perfect?
Answ er: Yes. Just lik e in the game w e studied with a discount factor ,
any split can be supported by a Nash equilibrium . Con sider the follow in g
strategy by player 2: reject an ything but the whole pie in the first period
and offer to keep the whole pie in the second. Pla yer 1’s best response in
the first period is to offer exactly the whole pie to player 2 because that
way he is guara nteed 0, while if he believes that player 2 will follow the
11. Strategic Bargaining 201
proposed strategy and he offers anyt hin g else then he will get
1
= −
1
.
¥
(c) Assume that =3. Find the subgam e perfect equilibrium of the game
and sho w in whic h w ay it depends on the values of
1
and
2
.
Answ er: Inthelastperiodplayer1makestheoffer in an ultimatum
game and will offer to k eep the whole pie:
1
=1and
2
=0,and
pla yer 2 is will accept (he’s indifferen t). Payoffswouldbe
1
=1− 2
1
and
2
= −2
2
.Goingbackwardstoperiod2,player2hastooffer at
least
1
=1− 2
1
to player 1 for him to accept, so the pay offsstarting
from the second period are
1
=1−3
1
and
2
=2
1
−
2
(player 1 gets
a piece of the pie equal to 1 −2
1
and because this is the second period
he incurs the cost
1
from the first period.) Finally, in period 1 play er 1
must offer pla yer 2 at least 2
1
−
2
so he will offer exactly that, pla yer
2 will accept the offer , an d the payoffs will be
1
=1− 2
1
+
2
and
2
=2
1
−
2
. ¥
5. Asymmetric P atience 1: Conside r a 3-period sequen t ial (alternating) bar-
gainin g model where two pla yers ha ve to split a pie worth 1 (starting with
player1makingtheoffer). No w the pla yers ha ve different discoun t factors,
1
and
2
.
(a) Compute the outcom e of the unique subgam e perfect equilibrium .
Answ er: In the third period pla yer 1 will get the whole pie and hence
the pa yoffs will be
1
=
2
1
and
2
=0. Moving back to the second period,
player 2 will offer player 1
1
and play er 1 will accept, so the pa yoffsare
1
=
2
1
and
2
=
2
(1−
1
).Movingbacktothefir s t period, player 1 will
offer to keep such that pla yer 2 will receiv e
2
=(1− )=
2
(1 −
1
)
implying that pla yer 1 gets
1
= =1−
2
(1 −
1
)=1−
2
+
1
2
. ¥
(b) Show that when
1
=
2
then player 1 has an advantage.
Answ er: In this case
1
=1−
2
+
1
2
=1− +
2
and
2
= −
2
,

202 11. Strategic Bargaining
implying that
1
−
2
=1− +
2
− ( −
2
)=1− 2 +2
2
=(1−)
2
+
2
0
implying that
1
2
. ¥
(c) What conditions on
1
and
2
give play er 2 an advantage? Why?
Answ er: For pla yer 2 to get an advan ta ge it must be that
1
2
which
implies using the answer in part a. above that 1 −
2
+
1
2
2
−
1
2
or 1 2
2
(1 −
1
). This condition means that
2
has to be significan tly
greater than
1
, meaning that player 2 has to be significantly more
patient for him to have an advantage. For example, if
2
is very close
to 1, then
1
has to be less than
1
2
for this condition to hold, and if
2
1
2
then player 2 will never ha ve an advantage. The patience has to
overcome the first and la st mover advantag e that player 1 has in this
case. ¥
6. Asymmetric Patience 2: Consid er the analysis of the infinite horizon bar-
gaining model in section 11.3 and a ssum e that the pla yers ha ve d ifferen t
discount factors
1
and
2
. Find the unique subgame perfect equilibrium us-
ing the same techniques, and sho w that as
1
and
2
becom e closer in values,
the solution you found converges to the solution derived in section 11.3 .
Answ er: Consider a subgame in which player 1 m a kes the offer. P layer 2
will not accept an offer that gives him less than
2
2
,implyingthat
1
≤ 1 −
2
2
(11.1)
and play er 2 will accept an offer that gives him at least than
2
2
, implying
that
1
≥ 1 −
2
2
(11.2)
By sym m etry, when player 2 makes the offer we obtain the symmetric in-
equalities,
2
≤ 1 −
1
1
(11.3)

11. Strategic Bargaining 203
and
2
≥ 1 −
1
1
(11.4)
Subtracting (11.2) from (11.1) yields
1
−
1
≤
2
(
2
−
2
) (11.5)
and similarly, subtracting (11.4) from (11.3) yields
2
−
2
≤
1
(
1
−
1
) (11.6)
But (11.5) and (11.6) together imply that
1
−
1
≤
2
(
2
−
2
) ≤
2
1
(
1
−
1
)
and because
2
1
1 it fo llows that
1
=
1
(=
1
) and
2
=
2
(=
2
).
Revisiting the inequalities above, (11.1) and (11.2) imp ly that
1
=1−
2
2
,
and (11.3) and (11.4) imply that
2
=1−
1
1
,
and from these last two equalities we obtain that in the unique subgame
perfect equilibrium , in the first period pla yer 1 receives
∗
1
=
1 −
2
1 −
1
2
and pla yer 2 receiv es 1 −
∗
1
=
2
(1−
1
)
1−
1
2
.Nowlet
1
= ,andlet
2
approac h
The denominator approac hes 1−
2
=(1−)(1+) and we get that
∗
1
=
1
1+
,
which is th e so lution w e obtained is section 11.3 for a symmetric discou nt
factor. ¥
7. Legislative Bargaining (revisited): Consider a finite period v ersion of
the Baron and Ferejohn legislative bargaining game with an odd number
of players and with a closed rule as described in section 11.4.1.
204 11. Strategic Bargaining
(a) Find the uniq u e sub ga m e perfect equilibriu m for =1.Also,find a
Nash equilibriu m that is not subga m e perfect.
Answ er: If =1then follo w ing a failed v ot e (a majorit y reject s the
proposer’s proposal) all the players receive a pay o ff of 0. Hence, lik e in
the Rubinstein game, the proposer will ask for all the surplus and a ma-
jorit y of pla yers will vote in fa vor. No other outcome can be supported
by a subgam e perfect equilibrium . There are many Nash equilibria. For
example, some player asks for at least
∗
∈ [0 1] of the surplus while
all other players will settle for nothing. Then any player 6= will offer
the amo unt
∗
, and nothing to the other players, and all the play ers
will v ote in favor of the proposal. ¥
(b) Find the unique subgame perfect equilibrium for =2with a discoun t
factor 0 ≤ 1 Also, find a N ash equilibrium tha t is no t su bga m e
perfect.
Answ er: If the proposal is not accepted in period 1 then period 2 will
ha v e the unique subgame perfect equilibrium described in part a. above.
This implies that in the first period, ever y player has an expected surplus
of
because they will be the proposer with proba bility
1
and will get
thewholesurplusof1.Thismeansthattheplayerwhooffer s in the first
period must offer at least
to
−1
2
other pla yers to form a m ajorit y
and have the proposal accepted. Hence, the proposing player will keep
1−
−1
2
to himself in the unique subgam e perfect equilibrium. Just lik e
in par t a. above, we can support an arbitrary division of the surplus
in a Nash equ ilib riu m by having some players com mit to incredib le
strategies. ¥
(c) Compare what the first period’s proposer receives in the subgam e per-
fect equilibrium yo u fou nd in pa rt (b) abo ve to w ha t a first period
proposer receiv es in the t wo-period t wo-person Rubinstein-Ståhl bar-
gaining gam e. Wh at intuitively accounts for the difference?
Answ er: In the two-period two-person Rubinstein-Ståhl bargainin g
game the proposing player 1 gets 1 − because player 2 can get the

11. Strategic Bargaining 205
whole pie in the second period. Notice that the difference bet ween the
pa y off in the Baron-Ferejohn model and the Rubinstein-Ståhl model is,
1 −
− 1
2
− (1 − )=
( +1)
2
2
.
As w e can see, the firstproposerhasalotmoresurplusintheBaron-
Ferejohn m odel. This is because the responder is not one player wh o
pla y s an ultimatum game in the secon d period, bu t a group of player
from whic h a majority needs to be selected. This lets the proposer pit
the responders against each other and capture more surplus. ¥
(d) Compare the subgame perfect equilibrium y ou found in part (b) above to
the solution of the infinite horizon model in section ??. What intuitively
accoun ts for the similarity?
Answ er: The share receiv ed b y the first proposer is the same as what
w e deriv ed in equation (11.8). The intuition is that the same forces are
at work: the larger the discount factor the more the proposer needs to
giveaway,andthemorepeoplethereare,themorehehastogiveaway.
Still, he gets to k e ep at least
1
2
because of the competitiv e nature of the
situation in whic h the responder s are put. ¥
