Towards a Homomorphic Machine Learning Big Data Pipeline for
the Financial Services Sector
Oliver Masters
1
, Hamish Hunt
1
, Enrico Steffinlongo
1
, Jack Crawford
1
, Flavio Bergamaschi
1
,
Maria Eugenia Dela Rosa
2
, Caio Cesar Quini
2
, Camila T. Alves
2
, Fernanda de Souza
2
, and Deise
Goncalves Ferreira
2
1
IBM Research, Hursley, UK
{oliver.masters,enrico.steffinlongo,jack.crawford}@ibm.com
{hamishhun,flavio}@uk.ibm.com
2
Banco Bradesco SA, Osasco, SP, Brasil
{maria.e.delarosa,caio.quini,camila.t.alves,fernanda.souza,deise.g.ferreira}@bradesco.com.br
Abstract. Machine learning (ML) is today commonly employed in the Financial Services Sector (FSS)
to create various models to predict a variety of conditions ranging from financial transactions fraud to
outcomes of investments and also targeted marketing campaigns. The common ML technique used for
the modeling is supervised learning using regression algorithms and usually involves large amounts of
data that needs to be shared and prepared before the actual learning phase. Compliance with privacy
laws and confidentiality regulations requires that most, if not all, of the data must be kept in a secure
environment, usually in-house, and not outsourced to cloud or multi-tenant shared environments.
This paper presents the results of a research collaboration between IBM Research and Banco Bradesco
SA to investigate approaches to homomorphically secure a typical ML pipeline commonly employed in
the FSS industry.
We investigated and de-constructed a typical ML pipeline used by Banco Bradesco and applied Homo-
morphic Encryption (HE) to two of the important ML tasks, namely the variable selection phase of the
model generation task and the prediction task. Variable selection, which usually precedes the training
phase, is very important when working with data sets for which no prior knowledge of the covariate set
exists. Our work provides a way to define an initial covariate set for the training phase while preserving
the privacy and confidentiality of the input data sets.
Quality metrics, using real financial data, comprising quantitative, qualitative and categorical features,
demonstrated that our HE based pipeline can yield results comparable to state of the art variable
selection techniques and the performance results demonstrated that HE technology has reached the
inflection point where it can be useful in batch processing in a financial business setting.
Keywords: homomorphic encryption; variable reduction; variable selection; feature selection; pre-
diction
1
Table of Contents
Towards a Homomorphic Machine Learning Big Data Pipeline for the Financial Services
Sector . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
Oliver Masters, Hamish Hunt, Enrico Steffinlongo, Jack Crawford, Flavio Bergamaschi,
Maria Eugenia Dela Rosa, Caio Cesar Quini, Camila T. Alves, Fernanda de Souza,
and Deise Goncalves Ferreira
1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
2 Background . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.1 CKKS in HElib . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.2 Homomorphic predictions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.3 Variable Selection via Logistic Regression . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
3 Implementation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
3.1 Pipeline Overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
3.2 Function Approximations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
3.3 HE logistic regression predictions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
3.4 Homomorphic variable selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
4 Experimental Evaluation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
4.1 Testing Environment . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
4.2 CKKS Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
4.3 Dataset preparation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
4.4 Results and discussion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
5 Conclusion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
6 Further Work . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
Acknowledgements . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
References . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
A Model Evaluation Metrics . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
2
1 Introduction
Homomorphic encryption (HE) promises to generally transform and disrupt how business is cur-
rently done in many industries such as, but not limited to, healthcare, medical sciences, and finance.
One particular area of interest and value to apply HE across numerous industries is in machine
learning (ML). The ability to compute directly on the encrypted data allows that data to be shared
in areas that were once considered impossible or highly undesirable due to data leaks through single
point of failure (individuals or systems with the authority to see the data) which could be insecure.
Today, organizations make far more use of vast amounts of aggregated data to be able to perform
data analytics and ML. Many organizations find themselves restricted from sharing data, internally
and externally, due to legislation, regulation, and their other need-to-know policies coming into
direct conflict with the need to collaborate by sharing the data (a.k.a. need-to-share). Approaches
leveraging homomorphic encryption can overcome these restrictions by allowing homomorphic data
aggregation intra- and/or inter-organization; meaning that a computation requiring the aggregated
data can be performed without other parties having access to data shared in the aggregation.
HE as a technology has undergone accelerated progress since Gentry’s influential work [13]
showed how to construct a fully homomorphic encryption scheme based on lattices. Several schemes
and algorithmic improvements have emerged since Gentry such as the BGV [5] and FV [12] schemes.
The community is aware that the technology is becoming adequately performant to be useful and/or
disrupt several areas [1]. In the last few years, the CKKS scheme [9] has emerged offering a more
natural setting for performing operations on approximate numbers. CKKS is thus generally more
suitable to analytics and ML problems.
The terminology Machine Learning, first introduced by Arthur Samuel in 1959 [25], today com-
prises several tasks with the fundamental goal of creating a model that can make predictions. Model
generation by learning is the main focus of ML and the motivation in doing this homomorphically
has been around for a few years. Many solutions have been shown to perform this task with varying
times from minutes to hours using different HE schemes [20,8,4,21,10,16]. However, practitioners
are aware that in a typical ML pipeline this is but one necessary task.
Our work consists of exploring two tasks in the ML pipeline that HE can aid in the sharing of
data. The first is running the prediction of a generated logistic regression model. This is the task
that is the re-usable part of the typical ML endeavor. Businesses will want to ensure that only
certain parts of the business will have access to the model and/or data. Although this tends to be
inherently performed in the learning aspect it has had little attention to as a separate facet and
metrics on it seem somewhat limited in the literature. Moreover, in previous works [14,6] the speed
of prediction was achieved through having the model itself unencrypted, thus only providing privacy
of the input data. This work explores the concept of keeping the generated model private in addition
to the data. The second task that we explore is performing variable reduction or more precisely
variable selection (a.k.a. feature selection in the literature). With real data, this is a very common
machine learning pipeline phase in the model generation and necessary to avoid overfitting of the
data and/or only perform learning with variables of importance thus reducing resource required.
To achieve our goals, we apply state-of-the-art techniques in homomorphic encryption and
ML. For our homomorphic encryption and computations, we use the homomorphic encryption
library HElib [15], explicitly making use of its CKKS capabilities in the work presented. Firstly, we
take an existing, encrypted logistic regression model that constitutes sensitive intellectual property
and demonstrate the feasibility of running a large number of encrypted prediction operations on
real, encrypted financial data while retaining acceptable performance with both 128 and 256 bits
3
of security. Secondly, we build on work by Bergamaschi et al. [2] by exploring the feasibility of
homomorphic variable selection.
2 Background
In this section, we will introduce the key concepts which will be required throughout this work. All
homomorphic computations were done using HElib’s CKKS capabilities that were introduced to the
library in 2018 [2,15]. This allows us to code using approximates of real numbers. To solve both ML
tasks of predicting and variable selection, this is required. The way we determine the importance
of a variable for variable selection is to use the evaluation of a logistic regression model trained on
that variable individually.
2.1 CKKS in HElib
The CKKS scheme [9] has provided a large change for certain problems of how we think about
applying HE. In HElib’s variant of the scheme the ciphertext mechanisms are mostly the same as
they are for the BGV scheme [2]. The main difference lies in the CKKS plaintext space which we
will take advantage of.
CKKS has a decryption invariant form of [hsk, cti]
q
=
˜
pt, where sk and ct are the secret key and
ciphertext vectors, respectively, [·]
q
denotes reduction modulo q into the interval (−q/2, q/2], and
˜
pt is an element that encodes the plaintext and includes also some noise. CKKS uses an element
˜
pt
of low norm, |
˜
pt| q. Decoding to a plaintext, pt, is given by
˜
pt = e + ∆ · pt where ∆ is a scaling
factor and, ideally, after performing our necessary computation we still have |e| < ∆.
Due to working with approximations of real numbers the scheme supports varying levels of
precision determined by the accuracy parameter r. The noise, e, introduced during the encoding
of the plaintext causes each operation performed in the CKKS scheme to be accurate up to an
absolute bound on the magnitude of the additive noise, namely 2
−r
.
The HElib implementation of the CKKS scheme maps to a plaintext space that is the integer
polynomial ring Z[X]/hΦ
m
(X)i where Φ
m
(X) is the m
th
cyclotomic polynomial with degree given
by Euler’s totient φ(m). The scheme provides encode and decode procedures to map the native
plaintext elements to and from plaintext complex vectors v = C
l
where l = φ(m)/2 determines the
number of complex numbers that can be packed into a single plaintext. For our purposes, we only
make use of the real part of the numbers.
2.2 Homomorphic predictions
Given a trained ML model, its primary purpose is the generation of an output estimate of whether a
given input has the condition or not. This is known as prediction. Many types of predictive models
can be considered to be another form of data which can be encrypted homomorphically.
Depending on the scenario there are choices to be made as whether the data, the model or both
are homomorphically encrypted. In all cases, the output will be encrypted as an operation between
a ciphertext or a plaintext with a ciphertext always results in a ciphertext.
The first proposal of a privacy preserving Encrypted Prediction as a Service (EPaaS) solution
was CryptoNets [14] in 2016. CryptoNets achieved 99% accuracy and a throughput of roughly 59000
predictions per hour.
4
When applying a prediction model in an HE context, careful consideration must be taken to
find a balance between the accuracy and the computational complexity. This is due to the natural
overhead that is introduced by encryption. Previous work has been carried out to reduce both the
limitation on the depth and breadth of the circuit as well as the latency of such applications.
One such notable work to produce a low latency, homomorphic neural network known as LoLa [6]
presents an application that achieves considerable speedups without sacrificing on the level of secu-
rity provided in previous attempts. This was achieved via the use of alternative data representations
during the computation process. This application exhibited the feasibility of performing homomor-
phic predictions however left the exploration of homomorphically performing the training of ML
models to further study.
It should be noted that these previous schemes do not perform the prediction using a homo-
morphically encrypted model thus making the prediction less computationally expensive.
2.3 Variable Selection via Logistic Regression
Variable selection is the process of deciding which of the variables (or features) of a given dataset are
important to be kept when generating a predictive model. This also determines the variables which
are not worth preserving as they have negligible or detrimental impact on the model’s predictive
quality [17,19].
Homomorphic model generation by learning is a topic of increasing interest due to the ability
to generate models with training data that is encrypted. This is important in scenarios where the
data used for the training is private. In particular medical data is considered highly confidential
and there is focus on applying HE to this sector. Another key industry in which data privacy and
ML techniques are of particular interest is the financial sector.
Most notably, the work [4,8,10,21] related to the 2017 iDASH competition [18] as well as [20,16,3]
explore the use of logistic regression on homomorphically encrypted data to generate models. These
achieve varying computation times for data samples of differing sizes. Applications range from 6
minutes for over 1500 samples containing 18 features in [20] to generating a model from over 420000
samples containing over 200 features in approximately 17 hours [16]. These works demonstrate
both the reality of generating a model homomorphically in a feasible amount of time as well as the
scalability of such methods to handle large datasets.
Our work focuses on the variable selection phase which precedes the training phase in a typical
ML pipeline. In addition, unlike previous work, our approach assumes and uses an empty covari-
ate set. This is very important when performing data analytics on data sets for which no prior
knowledge of the covariate set exists. Our solution provides a way to homomorphically determine
an appropriate initial covariate set for the training phase.
When attempting to predict a binary condition or attribute (also known as classification) based
on other attributes given (not necessarily binary themselves), logistic regression is a standard ML
technique employed.
In this work, we are only dealing with the case where the condition that we want to predict
is binary (i.e. with condition or without condition). The data, which one can consider to form a
matrix, consists of n records or rows of the form (y
i
, x
i
) with y
i
∈ {0, 1} and x
i
∈ R
d
. The aim
is to predict the value of y ∈ {0, 1} given the attributes x, and the logistic regression technique
5

postulates that the distribution of y given x is given by
Pr[y = 1|x] =
1
1 + exp
−w
0
−
P
d
i=1
x
i
w
i
=
1
1 + exp (−x
0
T
w)
,
where w ∈ R
d+1
is a fixed vector of weights and x
0
i
= (1|x
i
) ∈ R
d+1
is a feature vector. Given the
training data {(y
i
, x
i
)}
n
i=1
, we can therefore make predictions if we can find the vector w that best
matches this data, where the notion of best match is typically maximum likelihood. Such a weight
vector, w
∗
, can be expressed explicitly as
w
∗
= arg max
w
Y
y
i
=1
1
1 + exp
−x
0
i
T
w
·
Y
y
i
=0
1
1 + exp
x
0
i
T
w
where we use the probability postulate given above in conjunction with the following identity
1 −
1
1 + exp(−z)
=
1
1 + exp(z)
.
The formula for w
∗
can be written more compactly by setting y
0
i
= 2y
i
− 1 ∈ {±1} and
z
i
= y
0
i
· x
0
i
, then our goal is to compute or approximate
w
∗
= arg max
w
(
n
Y
i=1
1
1 + exp (−z
i
T
w)
)
= arg min
w
(
n
X
i=1
log
1 + exp
−z
i
T
w
)
.
For a candidate weight vector w, we denote the (normalized) loss function for the given training
set by
J(w)
def
=
1
n
·
n
X
i=1
log
1 + exp
−z
i
T
w
,
and our goal is to find w that minimizes that loss.
Nesterov’s Accelerated Gradient Descent. We use Nesterov’s accelerated gradient decent [23]
which has been used successfully and applied previously in [2]. It is a variant of the iterative method
used by Kim et al. in [20]. Let σ be the sigmoid function,
σ(x)
def
= 1/(1 + e
−x
),
then the gradient of the loss function with respect to w can be expressed as
∇J(w) = −
1
n
n
X
i=1
1
1 + exp (z
i
T
w)
· z
i
= −
1
n
n
X
i=1
σ
−z
i
T
w
· z
i
.
6
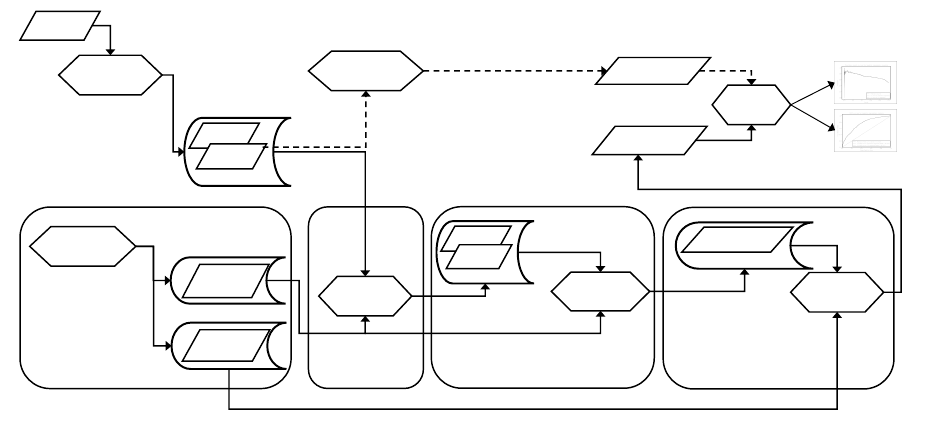
Untrusted Container
Trusted Container
Trusted Container
Simple
Key Management
Trusted Container
Financial
Data
Computation
Result
Data
Preparation
Data
Data
Unencrypted
Clear
Computation
Encode
Encrypt
Data
Data
Encrypted
Encrypted
Computati
on
Computation
Result
Encrypted
Decrypt
Decode
Computation
Result
Analysis
FHE Context
FHE Keys
Generator
Public key
+ Context
Secret key
+ Context
Secure Channel
Graphs
1
2
3
4
Fig. 1. Homomorphic and plaintext pipelines.
Nesterov’s method initializes two evolving vectors to the mean average of the input records.
Then each iteration computes
w
(t+1)
= v
(t)
− α
t
· ∇J
v
(t)
,
v
(t+1)
= (1 − γ
t
) · w
(t+1)
+ γ
t
· w
(t)
,
where α
t
, γ
t
are scalar parameters that change from one iteration to the next. The α parameter is
known as the learning rate and γ is called the moving average smoothing parameter. For how they
are set, see section 3.4.
3 Implementation
In this section, we will discuss our methodology for performing homomorphic predictions and ho-
momorphic variable selection. In the case of the logistic predictions, we provide a description of the
method used to efficiently pack data into CKKS ciphertexts as well as requisite function approxi-
mations employed. In the case of the variable selection, we provide greater detail of the technique
adopted for obtaining relevant scores for each variable as well as parameters and configuration of the
Nesterov gradient descent algorithm. We present the modular ML pipeline of our experimentation.
3.1 Pipeline Overview
Figure 1 illustrates the basic model of the computation and flow of data of the implemented
system, used for both prediction and variable selection. In this model, we have several parties
with the trusted parties operating in trusted containers (labeled 1, 2, and 4) and the untrusted
party operating in the untrusted container 3. Typically, this trust model would correspond to a
7
client-server relationship in which the server is considered to be acting under the honest-but-curious
attacker model.
The trusted container 1, hosted in a hardware security module, is responsible for key manage-
ment and generation of the public-private key pairs, and the key switching matrices required for
the computation, as described in [15]. For the sake of conciseness, we will henceforth refer to the
public key, the context, and the key switching matrices collectively as simply the public key.
Trusted container 2 is responsible for encrypting the plain data with the public key. The en-
crypted data is made available to container 3, the honest-but-curious untrusted environment where
the homomorphic computation can be performed. Both containers require and have access to the
public-key.
Trusted container 4 is responsible for decrypting the final results using the secret key which is
accessed through a secure channel.
Considering the flow of data through the system, firstly raw financial data is sanitized and
pre-processed by the Data Preparation module, which then flows into trusted container 2. The data
is then encoded according to the relevant Data packing method as described later on, which differs
depending on whether prediction or variable selection is being performed. The encoded data is then
encrypted using the public key and then sent to the untrusted container.
The untrusted container 3 performs whichever homomorphic computation is required by using
the public key and encrypted data. In the prediction case, this will be an operation between en-
crypted data and an existing encrypted model as described in 3.3. In the variable reduction case,
this will be a large number of logistic regression model trainings followed by a log loss computation
as described in 3.4. In both cases, the encrypted output is passed to the trusted container 4 for
decryption. Trusted container 4 will decrypt the result with the secret key and then process it
directly or pass it elsewhere for usage.
In addition to this workflow, figure 1 also contains more steps which would not be used in a
typical system, but that we employed for evaluation purposes. These can be seen in the cells which
are connected with dotted lines. The Clear Computation block performs analogous computations
to the Encrypted Computation block, except they are performed with standard methods entirely
on the plaintext data. The results of the Clear Computation block and the HE pipeline are then
compared using standard statistical techniques. It is from this final analysis step that the figures
seen in section 4.4 are derived.
3.2 Function Approximations
Our homomorphic computations necessitate the evaluation of several higher-order functions such
as sigmoid and logarithm. Despite the fact that addition and multiplication are the only operations
native to the CKKS scheme employed, we are able to use polynomial approximations of arbitrary
continuous functions. It was important to strike a balance between degree of polynomial approxi-
mation with higher degrees increasing the depth of the calculation and accuracy of approximation
which is harmed by lower-degree approximations. Due to the significant disadvantages inherent to
high-degree polynomials, in terms of both computation time and noise growth, we use the lowest-
degree approximations possible which still yield good results.
Sigmoid approximation. For sigmoid function approximation, we use the same low-degree poly-
nomial function in a bounded symmetrical range around zero as in [20,2], namely with degree-3
8

and degree-7 approximation polynomials in the interval [−8, 8]
SIG3(x)
def
= 0.5 − 1.2
x
8
+ 0.81562
x
8
3
and (1)
SIG7(x)
def
= 0.5 − 1.734
x
8
+ 4.19407
x
8
3
(2)
−5.43402
x
8
5
+ 2.50739
x
8
7
Logarithm approximation. We apply the same technique to derive a quartic polynomial ap-
proximation function for the composition log ◦ σ directly rather than composing approximations
for both logarithm and sigmoid, since this allows us to perform the required computation with
minimal computational depth. We again use an approximation minimizing mean squared difference
in [−8, 8]:
LOGSIG4(x)
def
= 0.000527x
4
− 0.0822x
2
+ 0.5x − 0.78 (3)
3.3 HE logistic regression predictions
In this section, we describe a general implementation to perform logistic regression predictions.
This is achieved by encoding and encrypting both model and data. More precisely, taking data
that was segregated for testing from a real financial dataset, the data was encoded and encrypted
then passed to the predictor. The predictor loads the required model and performs the prediction
algorithm. Essentially a inner product that is the input to a sigmoid function.
Data packing. To perform homomorphic logistic regression predictions, we require an encrypted
model and encrypted data. The model consists of a vector of weights β ∈ R
17
, where the 0
th
entry of
β is the bias term. In order to fit best with our homomorphic implementation, we simply replicate
each entry β
i
, 0 ≤ i ≤ 16, into its own ciphertext. That is to say, we let m
i
be an encryption of
the vector u
i
∈ C
l
where each entry of u
i
is equal to β
i
. For packing of the data, we describe first
the case where we have l predictions to perform, i.e. a set D of data where |D| = l. We pack all l
vectors {x
i
}
l
i=1
∈ R
16
into 16 ciphertexts by mapping the first entry of each x into one ciphertext,
the second entry of every x into another ciphertext, and so on.
Prediction. If we denote the resulting ciphertexts {c
i
}
16
i=1
, we can perform l predictions by com-
puting
σ
m
0
+
16
X
i=1
c
i
m
i
!
where is the entrywise product and σ is the sigmoid function (also computed entrywise in this
case). This amounts to an inner product operation on a vector of ciphertexts.
The resulting predictions will be one ciphertext which decrypts to a vector in C
l
corresponding
to l predictions. In order to perform n > l predictions, we simply partition the n data vectors into
d
n
l
e blocks, perform the prediction on each block, then concatenate the d
n
l
e vectors of size l at the
end. This can be performed completely in parallel for a large n.
The inner product can be computed natively due to our ability to perform additions and mul-
tiplications. However, subsequent to the inner product computation a sigmoid approximation is
applied to its result. As previously mentioned, the sigmoid function is approximated with a degree-
3 polynomial and evaluated on the output of the previous step depending on the level of accuracy
desired.
9

3.4 Homomorphic variable selection
Our variable selection method is to train a single-variable model for each of the variables in the
dataset then evaluate the quality of each model via a statistical score returning the scores to
a client. These scores are then used to sort the variables resulting in an ordering which should
roughly correspond to importance or predictive capability.
To perform this variable selection method homomorphically, we generate logistic regression
models and corresponding log loss scores for each of the variables in our dataset individually. In the
language of our logistic regression discussion in section 2.3, for each j with 1 ≤ j ≤ d we generate
a data set consisting solely of projections onto the j
th
variable. That is to say, we map each datum
(y, x) to (y, x
j
), then perform the logistic regression algorithm including log loss calculation on the
resulting data set for each j.
Data packing. A na¨ıve implementation of this might result in a large, albeit parallelizable, com-
putational requirement. However, we are able to take advantage of the slotwise vector operations
that the CKKS scheme gives us, packing each variable into an entry of a C
l
-vector, as discussed
in section 2.1. More explicitly, we perform the following transformation. For a dataset of size n,
(y
i
, x
i
)
n
i=1
, with each x
i
∈ R
d
, d ≤ l, and y
i
∈ {0, 1}, we create 2n vectors in C
l
in the following
way:
For each datum (y, x), compute y
0
= 2y −1 as before, then create a ∈ C
l
by setting a
i
= y
0
i≤d
,
which is a repetition of y
0
in the first d entries, padded with zeroes to the end of the ciphertext.
Next, generate the vector b ∈ C
l
by setting b
i
= y
0
x
i
i≤d
, which is a zero-padded version of x
with y
0
multiplied in. Now, we can use (a, b) ∈
C
l
2
in the same way as the z vectors are used in
section 2.3, thinking of d as 1 and exploiting the independence of entries of a CKKS ciphertext.
We henceforth refer to such vectors (a, b) as z with the understanding that all operations between
a and b are performed entrywise.
Initializing the algorithm. Since we need to use a small number of iterations, the initial values
of v, w are important to the convergence of the weights. We set them as the average of the inputs,
v
(0)
= w
(0)
=
1
n
n
X
i=1
z
i
as this yields better results than choosing them at random [2].
The number of iterations. The number of iterations, τ , that can be performed is very limited as
we are using a somewhat-homomorphic encryption scheme to implement the procedure on encrypted
data. For our implementation and tests, we used τ = 5 and τ = 6 iterations.
The α and γ parameters. The learning-rate parameter α was set just as in [20], namely in
iteration t = 1, . . . , τ we used α
t
= 10/(t + 1).
For setting the moving average smoothing parameter γ at each iteration, we used negative values
for gamma as suggested in [7]. Setting λ
0
= 0, we can compute for t = 1, . . . , τ
λ
t
=
1 +
q
1 + 4λ
2
t−1
2
and γ
t
=
1 − λ
t
λ
t+1
.
Values of γ for the first 6 iterations are γ ≈ (0, −0.28, −0.43, −0.53, −0.6, −0.65).
Log loss. Logarithmic loss is a statistical measure commonly used in ML for evaluating the quality
of a classification model which outputs probabilities. A log loss closer to zero implies a model with
10

greater predictive quality. This technique takes into account the level of certainty of the prediction
and compares it to the true value. For example, a probability prediction close to one will be rewarded
heavily if correct, but heavily penalized if incorrect.
In our logistic regression case with weights vector w and input data vectors z
i
, 1 ≤ i ≤ n, the
log loss function l is given by
l(w) = −
1
n
n
X
i=1
log
σ
z
T
i
w
In this work, we make extensive use of the log loss function for two reasons: as a cost function
of w to minimize during our logistic regression model fitting; and as a score by which to order
variables. To compute this homomorphically, we use the LOGSIG4 approximation (equation 3) to
give our (unscaled) log loss approximation function. We omit the
1
n
term for ease of calculation
since we are only concerned with the ordering resulting from these values.
LOGLOSS(w)
def
= −
n
X
i=1
LOGSIG4
z
T
i
w
(4)
Note that we also make use of the exact version of the log loss function in section 4 for assessing
the quality of models.
Decorrelation. In order to improve the quality of models obtained homomorphically or otherwise,
we apply decorrelation to the variables which is a standard technique in data analytics to improve
model stability and mitigate overfitting [19]. However, rather than blindly applying a decorrelation
policy during the data preparation phase (i.e. on the unordered set of variables), we delay the
decorrelation until after the variable ordering has been obtained. This post-processing phase is
advantageous to the resulting model as we are able to preferentially drop variables which are
considered by the ordering to have lower predictive capability.
The precise method that we use for removing correlated variables is as follows: given an ordering
of variables (V
1
, . . . , V
d
) where d is the number of variables, we consider the matrix M defined by
M
ij
= |ρ(V
i
, V
j
)|, where ρ(X, Y ) is the Pearson’s correlation coefficient between two variables X
and Y . We drop the variable V
j
if and only if there exists an entry in the j
th
column of the upper
triangle of M with value greater than or equal to 0.75, i.e. if and only if there exists i ∈ N, 1 ≤ i < j
such that M
ij
≥ 0.75.
Upon first glance this might appear to go against the spirit of a homomorphic variable selection
pipeline since the ρ values require the original data to be computed, however this is not the case.
Notice that for any variable ordering, the utility matrix M is formed simply by rearranging the
values of any other such matrix of correlation values. Thus, pre-computing the
d(d−1)
2
real numbers
in the upper triangle of M before performing the variable ordering gives us enough information to
perform our decorrelation procedure without needing access to the data again.
Note that performing decorrelation before the variable selection phase would not result in any
performance optimization, since the way in which we pack data into C
l
vectors means that we can
treat up to l variables without any slowdown. As can be seen in table 1, we always have l d.
4 Experimental Evaluation
The results from executing our pipeline are presented in this section. We primarily evaluate and
compare the quality of predictions as well as the quality of the variable selection process.
11

Firstly, we describe the configuration of our pipelines including hardware specifications and
HE scheme parameters. We then discuss and analyze the results of the implemented methodology
with comparisons to plaintext equivalents. Other metrics and methods were chosen to evaluate the
quality of predictions as well as those used to evaluate our method of performing variable selection.
The particular methods chosen were area under curve (AUC) and average precision (AP), detailed
descriptions of these metrics are in Appendix A.
4.1 Testing Environment
Our approach has been tested on a hardware and software environment commonly available in
the finance industry data centers and/or cloud settings, capable of high volume shared and multi-
tenant workloads. The hardware used for our tests is an IBM z14 LPAR supporting 64 simultaneous
threads over 64 cores, 1 TB RAM, and 1.2 TB HDD, running Linux Ubuntu 18.04 LTS.
4.2 CKKS Parameters
Parameters for the algebra used for CKKS were chosen to give at least 128 bit security while having
enough qbits to support our required computational depth. Unlike the BGV scheme, parameters for
the CKKS plaintext space in HElib are easier to find because there is no plaintext prime to consider.
Moreover, m as a power of two works better for the deep circuit of the variable selection because
the ciphertext sizes are a power of two, thus making the inherent FFTs that must be performed by
HElib more efficient. Although not recorded in this work, we found that non-power-of-two algebras
slowed the computation down considerably.
The parameters selected for the experiments, in particular the variable selection, differ from
those used by Bergamaschi et al. [2] because the security estimation in the newer version of HElib
3
is more conservative. The initial parameter value to select is the m
th
cyclotomic polynomial to use
as this is the main factor on the security level λ and on the number of slots in each ciphertext. As
mentioned previously, it is easier to select the value for this parameter in CKKS as the lack of a
plaintext prime means that the number of slots will always be l = φ(m)/2 as seen in table 1.
The value of the precision parameter r was set to 50 so as to ensure the highest level of precision
with the aim to generate a model of a greater predictive quality. We conducted some preliminary
investigations to determine a high value of r that we could use and not lead to decryption issues.
The next parameter to consider is qbits, the bitsize of the modulus of a freshly encrypted
ciphertext. Since we are using a somewhat HE scheme this needs to be larger for evaluation of
deeper circuits such as the variable selection, not so for homomorphic prediction. As seen in table
1, the number of bits used for prediction is 360 yet for the deeper circuit of variable selection we
must select qbits to be over 2000. As operations are performed upon a ciphertext, the noise increases
and this consumes the bits of modulus chain. It is important to ensure there are enough bits left
of the modulus chain to allow for decryption of the result without any wraparound occurring.
The final parameter shown in table 1 is c. This parameter determines the number of columns
of our key switching matrices. The key switching is used to relinearize the ciphertext after each
multiplication operation. This was selected to be 2 so as to minimize the size of the key switching
matrices which reduces the size of the files being sent across the pipeline as well as reducing the
computation time of the relinearization process.
3
commit 67abcebf1f8c1bae9d51c9352e6fef7d5b8d71a3
12
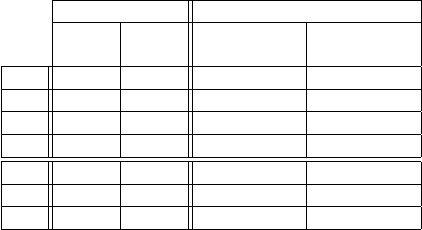
4.3 Dataset preparation
Table 1 specifies the parameters selected for the homomorphic prediction and homomorphic variable
selection experiments. The raw datasets used represents real financial transactions over a 24-month
period comprising a table of 360000 entries with 564 features (a mix of quantitative, categorical
and binary features). Although a large data set, the data is very sparse and the condition to
be modeled (propensity of contracting a bank loan) is a rare event in the dataset (only ∼ 1%)
where it would lead to a biased model that would underestimate the condition and overestimate
the non-condition [22]. During data preparation the input data was diligently sanitized for missing
values, categorical variable processing performed, and the data balanced; resulting in a balanced set
with approximately 7500 entries with 546 explanatory features. The plaintext reference model for
the prediction experiment contained 16 variables and was generated using the Python scikit-learn
library.
Table 1. CKKS parameters used for homomorphic prediction and homomorphic variable selection.
Prediction Variable Selection
128 bit 256 bit sig3 sig3
security security 5 steps 6 steps
m 21491 33689 262144(=2
18
) 262144(=2
18
)
r 50 50 50 50
qbits 360 360 2000 2400
c 2 2 2 2
φ(m) 21490 33060 131072(=2
17
) 131072(=2
17
)
l 10745 16530 65536(=2
16
) 65536(=2
16
)
λ 128 256 193 140
4.4 Results and discussion
We now present the results of the pipeline described in section 3 applied to both homomorphic
prediction and homomorphic variable reduction. These experiments were performed using the pa-
rameters given in table 1.
Homomorphic predictions. We evaluated the pipeline for homomorphic predictions with sev-
eral configurations. In terms of CKKS parameters, we performed predictions with parameters which
result in 128 and 256 bits of security. The prediction computation consisted of an inner product
followed by application of an approximated sigmoid function. In order to approximate the sigmoid
function while still minimizing the computation depth of performing predictions. Then we experi-
mented with our degree-3 sigmoid approximation, SIG3. The results of these prediction operations
were then analyzed by means of comparison with predictions run entirely in plaintext against the
same model.
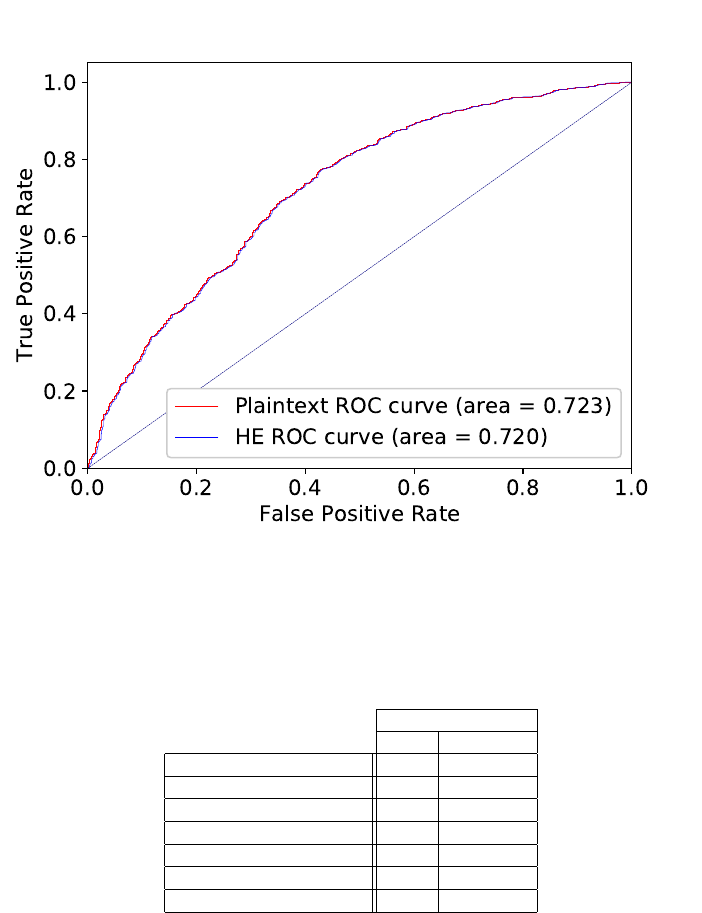
Figure 2 depicts the comparison between the predictions performed in plaintext and homomor-
phically. This is done by means of a ROC curve using a size 2271 sample with known condition to
test against. Both ROC curves are practically indistinguishable, demonstrating that any inaccu-
racies resulting from performing the predictions homomorphically do not significantly impact the
quality of the predictions. Table 2 shows performance information including memory usage for the
aforementioned prediction pipeline. Due to the low depth of computation required for performing
13
a logistic regression prediction operation, our solution achieves acceptable performance even in
the case of 256 bit security. Based on these results, selecting SIG3 provides the solution with the
adequate balance of accuracy and performance.
Fig. 2. ROC curve for plaintext and homomorphic prediction.
Table 2. CPU time and RAM usage of prediction.
Prediction Security
128 bit 256 bit
# Predictions per thread 10745 16530
# Threads 1 1
Encrypted Model size 40 MB 61 MB
Model input time 1 sec 1.3 sec
Encrypted Data size 37 MB 57 MB
Data input time 0.8 sec 1.2 sec
Prediction time 5.4 sec 9.4 sec
Homomorphic variable selection. We performed extensive experimentation in order to deter-
mine the quality of the homomorphic log loss calculations (section 3.4) compared to a fully-plaintext
pipeline which performs similar calculations. In this experimentation, we consider not the log loss
values themselves, but the quality of relative ordering which results from sorting based on these
values. Once an adequate set of parameters were derived for homomorphic log loss calculations,
14
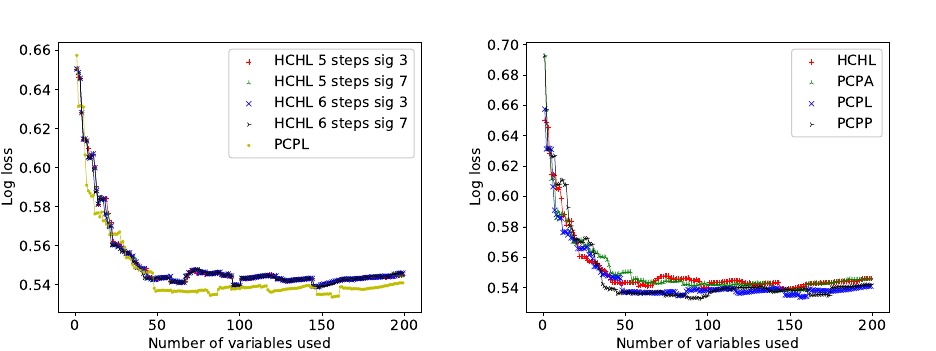
Fig. 3. Log loss for several homomorphic parameters. Fig. 4. Log loss for HE and plain.
we compared the results with various different plaintext-based orderings, namely ordering by AUC
and by AP.
Our method for evaluating the quality of the selected ordering was as follows. We took the first k
variables ordered by score, then used only these k variables to create a penalized logistic regression
model. We then evaluated the quality of the resultant model using 10-fold cross-validation to derive
a value for the typical scores: AUC, AP, and log loss. This procedure was carried out for each k
between 1 and 200. The results were then plotted on a scatter to evaluate any trends of differing
performance.
The convention used for the curves with four-letter labels (e.g. HCHL) in the graphs below is
the following. The first two letters indicate how the variable selection was computed; either HC
or PC for homomorphically computed or plaintext computed, respectively. The third letter H or
P indicate how ordering score was calculated, namely, homomorphically or in the plain. The last
letter indicates which metric was used for ordering (computing a score). This letter can take L, A
or P for ordering by log loss, AUC, or AP, respectively. Thus in combination, the last two letters
should be read as how the variable ordering was performed, e.g. HL for homomorphic log loss or
PL for plaintext log loss.
The first step in our assessment was to compare how homomorphic variable selection by logistic
regression ordered by homomorphic log loss (HCHL) really compares with the plaintext version
of variable selection by logistic regression ordered by plaintext-computed log loss (PCPL). This
comparison is illustrated in figure 3. Furthermore, we compared variations of the different HCHL
configurations, as described in section 4.2. The figure shows the comparison between different
numbers of Nesterov steps and different degrees of sigmoid approximations, alongside PCPL as a
baseline for comparison. It is clearly shown that ordering by log loss homomorphically is compa-
rable to computing it in the plain. We can also see that the HCHL configurations have negligible
difference. This is significant because of the consequences of requiring a higher depth of computa-
tion; namely its considerable effect on computation time and the adverse impact that the requisite
increase in qbits has on security. Nonetheless, for all remaining evaluations, we used the degree-7
sigmoid and 6 Nesterov steps.
15
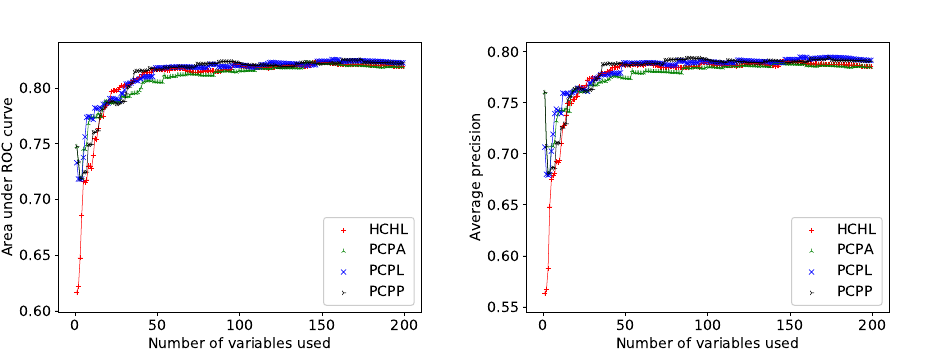
Fig. 5. Evaluation by AUC. Fig. 6. Evaluation by average precision.
Contemporary metrics commonly used for evaluation are AUC and AP. As discussed in ap-
pendix A, these are considered computationally heavy to implement homomorphically. However,
we compare the performance of ordering with these metrics in plaintext only. This comparison is
performed by measuring against all three of the aforementioned evaluation scoring methods. Eval-
uation by log loss can be seen in figure 4, AUC in figure 5, and AP in figure 6. All three of these
figures support the same conclusion: there is not significant difference between the different methods
of ordering, including the homomorphic methodology. One can read from any of the figures that
by around the time the 50 best-scoring variables have been included the model quality stabilizes at
around the same level.
Table 3 depicts the performance of the homomorphic variable selection with log loss ordering
comparing 5 and 6 Nesterov steps with degree-3 sigmoid approximation. These were run with the
algebras given in table 1. The 6 step version requires deeper computation, thus requiring an algebra
with a larger value for qbits. Consequently the ciphertexts are larger resulting in higher memory
usage than the 5 steps version. In both cases, increasing the number of threads decreases the running
time. However, in the shared and multi-tenant environment we observed that using more than 48
threads for computation did not further decrease the running time of the training phase, which is
a deep computation. This behavior is likely caused by memory locality issues resulting from the
large ciphertexts required. Since there is negligible difference in the quality of the results for 5 and
6 Nesterov steps as seen in figure 3, we choose 5 steps as a good compromise between memory
usage, performance, and quality of the results.
5 Conclusion
To progress towards a real-world ML pipeline, we investigated two common pipeline tasks. These
tasks need to be further considered when assessing if HE can be utilized to address whether data
can be aggregated. We have demonstrated that predictions can be performed in a typical business
setting with a powerful architecture in a reasonable amount of time for realistic workloads using
real financial data.
16
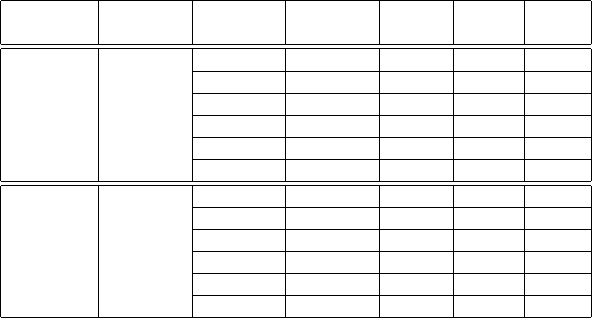
Table 3. CPU time and RAM usage of the degree-3 sigmoid with 5-6 Nesterov iterations vs. number of threads.
# Nesterov Data input # Threads Data input Training LogLoss RAM
iterations ciphertext time time time usage
5 64 GB
64 30 s 6062 s 217 s 228 GB
48 37 s 6000 s 205 s 220 GB
32 47 s 6186 s 231 s 217 GB
24 62 s 6467 s 280 s 210 GB
16 92 s 7255 s 388 s 206 GB
8 180 s 9491 s 784 s 200 GB
6 80 GB
64 32 s 9584 s 295 s 284 GB
48 58 s 9481 s 273 s 271 GB
32 58 s 9658 s 303 s 260 GB
24 75 s 9920 s 349 s 257 GB
16 113 s 11349 s 502 s 252 GB
8 218 s 15119 s 987 s 243 GB
Note: The timings in this table are for reference only as the HE code implementation was focused on achieving
numerical fidelity and adequate security.
Prediction on the encrypted reference model took less than 10 seconds with a security level of
256 bits. It was shown that over 16500 predictions can be performed in this time. Variable selection,
while preserving the privacy and confidentiality of the input data, took 1 hour and 43 minutes to
perform for a security level above 128 bits, which is adequate considering that most training tasks
run as batch processes. To achieve these levels of security, we used algebras not previously used
in related work [2] with m = 2
18
allowing for variable selection to be performed for the depth
required. The CKKS scheme has demonstrated to be invaluable to achieving good accuracy despite
its approximate nature, and with HElib it is now possible to have high accuracy by having the r
parameter set as high as 50.
Moreover, we have shown through comparison that log loss is an adequate metric for ordering
during the homomorphic variable selection. The experimentation demonstrated comparable results
to ordering by common ML metrics such as AUC or AP. This is a good result as log loss is considered
to be of low depth computationally as opposed to homomorphically calculating the other metrics.
6 Further Work
Due to time constraints, we were not able to explore performing the decorrelation homomorphically.
This would be of interest and the next logical step to attempt to tie together a more complete
machine learning pipeline. This might involve homomorphic calculations of correlation coefficients
such as the Pearson correlation coefficient used in this work, then elimination of variables with a
sufficiently high correlation. At the time of writing, the authors are unaware of any works which
attempt to achieve this and any such scheme would certainly push the depth of computation beyond
what this work performed.
Other future works may include attempting to calculate other model scores such as AUC or
AP in a novel homomorphic way, the latter of which might be of particular interest for heavily
imbalanced datasets. However, the homomorphic application of various threshold values may prove
problematic and high-depth in the absence of any innovative scheme for efficiently doing so.
17
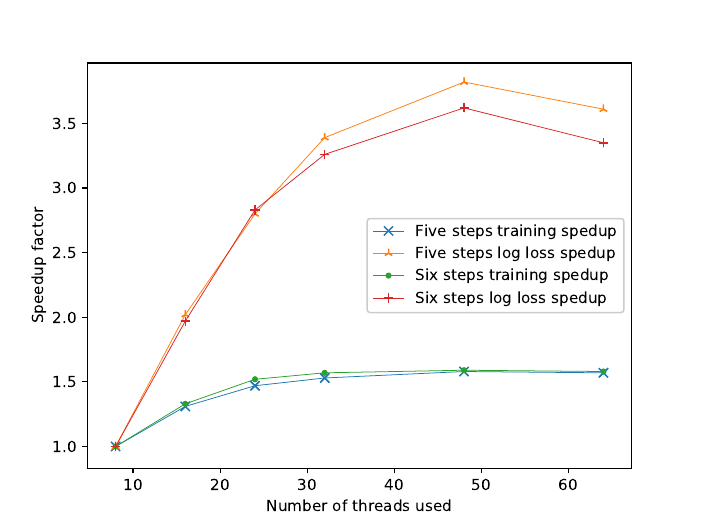
Fig. 7. Computation speed-up of training and log loss versus the number of threads.
It is reasonable to expect that more complete ML pipelines would require higher depth of
computation thus necessitating the requirement for bootstrapping. This would need to be taken
into consideration in implementation.
18
Acknowledgements
This research was part of the collaboration between IBM Research and Banco Bradesco SA to in-
vestigate the feasibility of utilizing homomorphic encryption technology to protect and preserve the
privacy and confidentiality of financial data utilized in machine learning based predictive modeling.
The views and conclusions contained in this document are those of the authors and should not be
interpreted as representing the official policies, either expressed or implied, of Banco Bradesco SA.
References
1. Archer, D., Chen, L., Cheon, J.H., Gilad-Bachrach, R., Hallman, R.A., Huang, Z., Jiang, X., Kumaresan, R.,
Malin, B.A., Sofia, H., Song, Y., Wang, S.: Applications of homomorphic encryption. Tech. rep., Homomorphi-
cEncryption.org (July 2017)
2. Bergamaschi, F., Halevi, S., Halevi, T.T., Hunt, H.: Homomorphic training of 30, 000 logistic regression models.
In: Applied Cryptography and Network Security - 17th International Conference, ACNS 2019, Bogota, Colombia,
June 5-7, 2019, Proceedings. pp. 592–611 (2019)
3. Blatt, M., Gusev, A., Polyakov, Y., Rohloff, K., Vaikuntanathan, V.: Optimized homomorphic encryption solution
for secure genome-wide association studies. IACR Cryptology ePrint Archive 2019, 223 (2019)
4. Bonte, C., Vercauteren, F.: Privacy-preserving logistic regression training. BMC Medical Genomics 11((Suppl
4)) (2018)
5. Brakerski, Z., Gentry, C., Vaikuntanathan, V.: (leveled) fully homomorphic encryption without bootstrapping.
ACM Transactions on Computation Theory 6(3), 13:1–13:36 (2014)
6. Brutzkus, A., Gilad-Bachrach, R., Elisha, O.: Low latency privacy preserving inference. In: Proceedings of the
36th International Conference on Machine Learning, ICML 2019, 9-15 June 2019, Long Beach, California, USA.
pp. 812–821 (2019)
7. Bubeck, S.: ORF523: Nesterov’s accelerated gradient descent. https://blogs.princeton.edu/imabandit/2013/
04/01/acceleratedgradientdescent, accessed January 2019 (2013)
8. Chen, H., Gilad-Bachrach, R., Han, K., Huang, Z., Jalali, A., Laine, K., Lauter, K.: Logistic regression over
encrypted data from fully homomorphic encryption. BMC Medical Genomics 11((Suppl 4)) (2018)
9. Cheon, J.H., Kim, A., Kim, M., Song, Y.S.: Homomorphic encryption for arithmetic of approximate numbers. In:
Advances in Cryptology - ASIACRYPT 2017 - 23rd International Conference on the Theory and Applications of
Cryptology and Information Security, Hong Kong, China, December 3-7, 2017, Proceedings, Part I. pp. 409–437
(2017)
10. Crawford, J.L.H., Gentry, C., Halevi, S., Platt, D., Shoup, V.: Doing real work with FHE: the case of logistic re-
gression. In: Proceedings of the 6th Workshop on Encrypted Computing & Applied Homomorphic Cryptography,
WAHC@CCS 2018, Toronto, ON, Canada, October 19, 2018. pp. 1–12 (2018)
11. Davis, J., Goadrich, M.: The relationship between precision-recall and ROC curves. In: Machine Learning, Pro-
ceedings of the Twenty-Third International Conference (ICML 2006), Pittsburgh, Pennsylvania, USA, June 25-29,
2006. pp. 233–240 (2006)
12. Fan, J., Vercauteren, F.: Somewhat practical fully homomorphic encryption. IACR Cryptology ePrint Archive
2012, 144 (2012)
13. Gentry, C.: Fully homomorphic encryption using ideal lattices. In: Proceedings of the 41st Annual ACM Sympo-
sium on Theory of Computing, STOC 2009, Bethesda, MD, USA, May 31 - June 2, 2009. pp. 169–178 (2009)
14. Gilad-Bachrach, R., Dowlin, N., Laine, K., Lauter, K.E., Naehrig, M., Wernsing, J.: Cryptonets: Applying neu-
ral networks to encrypted data with high throughput and accuracy. In: Proceedings of the 33nd International
Conference on Machine Learning, ICML 2016, New York City, NY, USA, June 19-24, 2016. pp. 201–210 (2016)
15. Halevi, S., Shoup, V.: HElib - An Implementation of homomorphic encryption. https://github.com/homenc/
HElib (Accessed August 2019)
16. Han, K., Hong, S., Cheon, J.H., Park, D.: Efficient logistic regression on large encrypted data. IACR Cryptology
ePrint Archive 2018, 662 (2018)
17. Hastie, T., Friedman, J.H., Tibshirani, R.: The Elements of Statistical Learning: Data Mining, Inference, and
Prediction. Springer Series in Statistics, Springer (2001)
18. iDASH: Integrating Data for Analysis, Anonymization and SHaring (iDASH). http://www.humangenomeprivacy.
org
19
19. James, G., Witten, D., Hastie, T., Tibshirani, R.: An introduction to statistical learning, vol. 112. Springer (2013)
20. Kim, A., Song, Y., Kim, M., Lee, K., Cheon, J.H.: Logistic regression model training based on the approximate
homomorphic encryption. IACR Cryptology ePrint Archive 2018, 254 (2018)
21. Kim, M., Song, Y., Wang, S., Xia, Y., Jiang, X.: Secure logistic regression based on homomorphic encryption:
Design and evaluation. JMIR Med. Inform. 6(2), e19 (2018)
22. King, G., Zeng, L.: Logistic regression in rare events data. Political Analysis 9, 137–163 (2001)
23. Nesterov, Y.: Introductory Lectures on Convex Optimization - A Basic Course, Applied Optimization, vol. 87.
Springer (2004)
24. Provost, F.J., Fawcett, T., Kohavi, R.: The case against accuracy estimation for comparing induction algorithms.
In: Proceedings of the Fifteenth International Conference on Machine Learning (ICML 1998), Madison, Wisconsin,
USA, July 24-27, 1998. pp. 445–453 (1998)
25. Samuel, A.L.: Some studies in machine learning using the game of checkers. IBM Journal of Research and
Development 3(3), 210–229 (1959)
26. Su, W., Yuan, Y., Zhu, M.: A relationship between the average precision and the area under the ROC curve.
In: Proceedings of the 2015 International Conference on The Theory of Information Retrieval, ICTIR 2015,
Northampton, Massachusetts, USA, September 27-30, 2015. pp. 349–352 (2015)
27. Zweig, M.H., Campbell, G.: Receiver-operating characteristic (roc) plots: a fundamental evaluation tool in clinical
medicine. Clinical Chemistry 39(4), 561–577 (1993)
20
Appendix A Model Evaluation Metrics
In section 3.4, we introduced and selected log loss as the metric for the ordering as it is a relatively
simple-to-compute measure that can be calculated homomorphically. To demonstrate its benefits
as a good common metric, we compared log loss to two other common metrics used to evaluate
machine learning models.
Area under curve. The receiver operating characteristic (ROC) curve is a standard tool in eval-
uating the performance of predictive models. The ROC space is typically defined as [0, 1]
2
where
a point (a, b) ∈ [0, 1]
2
has the false positive rate a and the true positive rate b of a given set of
binary predictions. For a set of probability predictions, it is typical to trace out the curve in the
ROC space parameterized by a threshold value. Attributes of the ROC curve, including the area
under the curve (AUC) are considered to be superior measures of the quality of a set of predictions
compared to a single accuracy value [27,24].
Average precision. Precision-recall (PR) curves are another tool similar in use to ROC curves,
but are more frequently used in information retrieval or situations in which the two classes are
imbalanced in the dataset. With PR curves, a similar parameterization on threshold value is per-
formed, but the points in [0, 1]
2
are (precision, recall) pairs instead of (false positive rate, true
positive rate) pairs. The method of taking the area under this curve as a metric, known as the
average precision (AP), is also a common practice. PR and ROC curves have been shown to have
strong links to each other for a given predictor [11] as well as a direct relationship shown by Su et
al. [26] between the AP and AUC scores.
In this work, we experimented with using AUC, AP, and log loss for selecting models and
evaluating quality of derived models. However, we do not compute AUC or AP homomorphically for
the purpose of variable ordering as this would require the application of a large number of threshold
function approximations; likely requiring an extremely high-depth computation in comparison to
our fourth-order log loss approximation in equation (4).
21
