
A
Dynamic Programming Algorithm to Find
All
Solutions in a Neighborhood of the Optimum
MICHAEL
S.
WATERMAN*
Depurtment
of
Muthemutics, University
of
Southern California
,
Los
A ngeles, Culiforniu 90089
-I I
I3
AND
THOMAS H. BYERS
Digitul Reseurch Inc.,
P.O.
Box 579, Pacific Grove, Culiforniu 93950
Received
I4
Junuury 1985: revised
22
Murch 1985
ABSTRACT
Just after he introduced dynamic programming, Richard Bellman with R. Kalaba in
1960
gave a method for finding Kth best policies. Their method has been modified since
then, but it is still not practical for many problems.
This
paper describes a new technique
which modifies the usual backtracking procedure and lists all near-optimal policies.
This
practical algorithm is very much in the spirit
of
the original formulation
of
dynamic
programming.
An
application to matching biological sequences
is
given.
INTRODUCTION
Finding near-optimal policies for dynamic programming models
is
usually
stated in terms of searching for the first, second,.
. .
,
Kth shortest paths
between a specified origin and destination
through
a directed, acyclic net-
work.
A
near-optimal solution is such a path whose length is within a
specified distance
or
neighborhood of the optimum. Thus, the set of near-
optimal paths includes the optimal path(s), whereas a set of paths generated
from heuristic or approximate methods may not. Recently we presented
a
new algorithm for finding
all
paths from an origin to a destination whose
length is within a specified distance of the shortest path(s)
[2].
Details of
implementation and comparison with Kth shortest path methods will also be
given here.
This
algorithm
was
motivated by a study of the evolutionary distance
problem
in
molecular biology. In
this
context, dynamic programming meth-
-b
*Support provided by
the
System Development Foundation.
MATHEMATICAL BIOSCIENCES
77:179-188 (1985)
179
OElsevier Science Publishing
Co.,
Inc.,
1985
52
Vanderbilt Ave., New York, NY
10017 0025-5564/85/$03.30

180
MICHAEL
S.
WATERMAN AND THOMAS H. BYERS
ods
are used to investigate evolutionary relationships between two DNA
sequences [20]. Analysis by Kth shortest path methods was not practical.
This
application is discussed below.
Pollack [16,17] and Dreyfus [4] provide surveys
of
currently available Kth
shortest path methods for directed, acylic networks. Bellman and Kalaba [l],
later modified by Fan and Wang [7], use forward dynamic programming to
find Kth best paths. Dreyfus [4] modifies the minimum tree technique of
Hoffman and Pavley [12] to yield a new algorithm. Dreyfus also demon-
strates its superiority to the algorithm of Bellman and Kalaba. The algorithm
is essentially a forward dynamic approach and uses both node labels and arc
labels to find K best paths. Fox [9-111 and Lawler [13] present slight
improvements
of
the Hoffman-Pavley-Dreyfus algorithm for certain net-
works by suggesting the use of special data structures called heaps in order to
increase computational efficiency. Elmaghraby [6] presents another dynamic
programming formulation, which is reviewed by Yen [23]. Minieka and Shier
[14] develop, and Shier [18,19] refines, a path algebra approach. Neither
algorithm is
as
good
as
that of Hoffman and Pavley (or its modification) in
terms
of
computational and storage requirements.
The new algorithm described in
this
paper is at least
as
fast
as
any
previously described method and requires much less storage. It is,
in
fact, the
first practical algorithm for these problems. The importance of this new
algorithm is to allow sensitivity analysis, robustness studies, or simple ap-
proximations
to
complex solutions to actually be obtained.
This
has not
previously been possible.
ALGORITHM
The object
of
the “shortest path problem”
is
to locate the shortest path
from node
1
to node
N
in
an acylic network of
N
nodes and
A
arcs. Each
arc
(i,
j)
has
an
associated weight
t(i,
J).
Dynamic programming,
as
de-
scribed in Dreyfus and Law [5] and Denardo [3], solves
this
problem by
recursively solving many optimization problems. Nodes
i
are labeled with
f(
i),
the length of the shortest path from node
i
to node
N.
Bellman’s insight
was
his famous principle of optirnality: “subpaths
of
optimal paths are
themselves optimal.”
This
is embodied
in
the recursion
f(
i)
=
min{
t(
i,
j)
+f(
j)
:
(i,
j)
an arc}.
The idea is that to reach
i
from
N,
the last step is from some node
j.
The
node
j
must be reached in an optimal manner if
j
is
on
an optimal path
from
N
to
i.
It only remains to note that
f(N)
=
0
is required to start the
recursion. The subject of
this
paper is to give a new algorithm for near-opti-
mal paths.

DYNAMIC PROGRAMMING ALGORITHM
181
Whereas previous algorithms find
K
shortest paths, the new algorithm
requires some percentage corresponding to an interval
e
above the optimal
length
f(1)
from the user. If a
p%
class
of
near-optimal paths is desired, then
e
is equal to
(p/100)f(l).
All paths less than or equal to quantity
f(l)+
e
are then found by the algorithm.
This
is convenient in problems where the
corresponding
K
is unknown and/or large.
While recursively calculating the node labels
f(i),
no
“pointer” or deci-
sion information needs to be kept. These node labels are found by working
backwards from node
N
until node
1
is labelled. The new algorithm then
performs a depth-first search with stacking, starting at node
1
and continuing
until all near-optimal paths are output.
Consider a node
x
not equal to the destination. Some path
P
with
cumulative distance
d
has led us to node
x
from node
1.
The test for entry of
the arc
(x,
y)
and distance
d
onto the stack now takes the general form, for
all
(x,
y)
E
A,
where
d
is the cumulative distance to node
x
from node
1
by path
P
(not
necessarily by shortest path),
t(x,
y)
is the distance from node
x
to node
y,
and
f(y)
is the optimal remaining distance to node
N
from node
y.
The algorithm eventually constructs a path
P
of length
d
from node
1
to
node
N.
Then
P
and
d
are output and the stack is examined to see
if
other
near-optimal paths exist. Hence the algorithm performs a last in, first out or
depth-first search.
To
justify the algorithm, suppose the algorithm has generated a path
P
of
length
d
from node
1
to node
x.
The arc
(x,
y)
added to path
P
is
on
at
least one near-optimal path
if
and only
if
d
+
t(x,y)+f(y)
~f(l)+
e,
since
the best path from
y
to
N
has length
f(y).
Note that ties in path lengths present
no
special problems. It is important
to see that an arc is not stacked unless it lies
on
some near-optimal path.
Also, the test
(*)
is never performed more than once for each node
on
any
particular near-optimal path.
EXAMPLE
>’
Consider the acyclic network given in Figure
1
with arc lengths
t(
i,
j)
and
nodes
A
through
I,
where nodes
A
and
I
represent origin and destination.
Numbers above each node
[
f(
i)]
represent the shortest length from that node
to node
I.
Suppose the user requests
all
paths within
20%
of the optimal path
length
13,
which is the node label at node
A.
This
percentage implies an
upper bound of 15.6 The ordered path array
P
contains the nodes of the
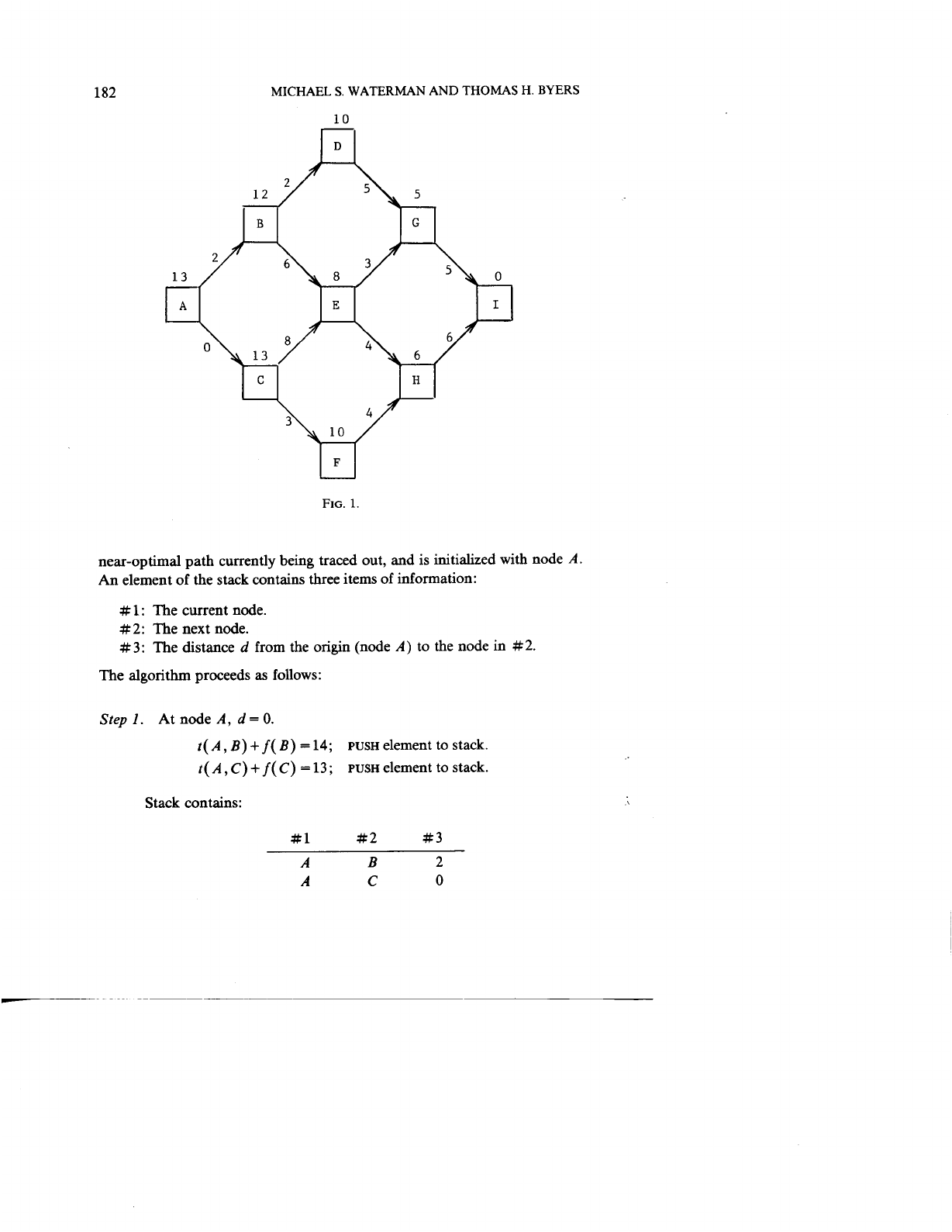
182
MICHAEL
S.
WATERMAN
AND
THOMAS
10
5\.
5
H.
BYERS
FIG.
1.
near-optimal path currently being traced out, and is initialized with node
A.
An element of the stack contains three items of information:
#1:
The current node.
#2:
The next node.
#3:
The distance
d
from the origin (node
A)
to the node in
#2.
The algorithm proceeds
as
follows:
Step
1.
At node
A,
d
=
0.
t(
A,
B)
+
f(
B)
=
14;
t(
A,
C)
+f(
C)
=
13;
PUSH
element to stack.
PUSH
element to stack.
Stack contains:
#1 #2 #3
A
B
2
A
C
0
c

DYNAMIC PROGRAMMING ALGORITHM
183
Step
2.
POP
last element
of
stack and put “next node” stored in
#2
into
P
array
=
(A,
C).
At node
C,
d
equals the distance stored in
#3
or
d
=
0.
d
+
t(
C,
E)
+f(
E)
=16;
d+t(C,F)+f(F)=13;
PUSHelement.
no action taken.
Stack contains:
#1
#2
#3
A
B
2
C
F
3
Step
3.
POP
last element.
P
=
(A,
C,
F).
At node
F, d
=
3.
d
+
f(
F,
H)
+
f(
H)
=
13;
PUSH
element.
Stack contains:
#1
#2
#3
A
B
2
F
H
7
Step
4.
POP
last element.
P
=
(A,
C,
F,
H).
At node
H,
d
=
7.
d
+
f(
H,
I)
+f(
I)
=
13;
PUSH
element.
Stack contains:
#I
#2
#3
A
B
2
H
I
13
Step
5.
POP
last element.
P
=
(A,
C,
F,
H,
I).
Node
I
has been reached,
so
path
P
with
d
=
13
is
output. Stack now contains:
#1
#2
#3
A
B
2
Step
6.
POP
element.
P
=
(A,
B),
d
=
2.
d
+
t(
B,
D)+f(
D)
=14;
PUSH
element.
d
+
t(
B,
E)
+f(
E)
=
16;
no action taken.

184
MICHAEL
S.
WATERMAN AND THOMAS H. BYERS
Stack contains:
#1
#2 #3
B
D
4
Step
7.
POP
element.
P
=
(A,
B,
D),
d
=
4.
d
+
t(
D,
G)
+
f(
G)
=
14;
PUSH
element.
Stack contains:
#1
#2
#3
D
G
9
Step
8.
POP
element.
P
=
(A,
B,
D,
G),
d
=
9.
d
+
t(
G,
I)
+
f(
I)
=
14;
PUSH
element.
Stack contains:
#1
#2
#3
G
I
14
Step
9.
so
path
P
with
d
=
14
is output. Stack is empty,
so
terminate.
POP
element.
P
=
(A,
B,
D,
G,
I).
Node
I
has been reached,
To summarize, the near-optimal paths from node
A
to node
I
are:
A+C+F+H+I,
length13,
A
+
B
+
D
+
G
-,
I,
length
14.
DISTANCE BETWEEN BIOLOGICAL SEQUENCES
Dynamic programming methods
to
compare macromolecular sequences
started with Needleman and Wunsch [15], who introduced a similarity
measure. Subsequently many modifications and advances have been made.
A
recent review by Waterman [22] discusses these methods as well as several
which are not based on dynamic programming. The basic problem
is
to
find
the minimum weighted sum of substitutions and insertion/deletions to
change the sequence
x
=
x1x2..
.
x,
into
y
=
yly2..
.
y,,,.
Let
d(
x,
y)
denote
the distance between the letter
x
and the letter
y;
d(x,y)
can also be
considered to be the weight associated with a substitution of
y
for
x.
Also
let

DYNAMIC PROGRAMMING ALGORITHM
185
w(
k)
be the weight associated with a deletion (or insertion) of
k
consecutive
letters.
Let
p(x,y)
denote the distance between
x
and
y.
Define
The utility
of
dynamic programming for sequence comparisons is that it
allows recursive calculation of
pi,,:
p.
.
=
min{
min
{
pk.j
+
w(
i
-
k)}
,
1.J
Ickci-l
Since
pfl,m
=
p(x,y),
it can be seen that
p(x,y)
can be found in
0(n3)
steps
when
n
=
m.
If
w(k)
=
ak
+
b,
the computation can be reduced to
O(n2)
steps.
The biologically correct values for
d(
-)
and
w(
.)
are not precisely known,
although there are attempts to infer them from data. In addition, unknown
biological constraints frequently act
so
that a
"
nonoptimal" sequence align-
ment is the biologically correct alignment. The algorithm described in
this
paper was developed to help with these difficulties.
As
above, the algorithm is to find all alignments within
e
of
p,,,,
the
optimal alignment. It is possible to view
p,,,
as
the length of the shortest
path from
(0,O)
to
(n,
m).
The algorithm described above solves
this
problem
and was first presented with a specific application [21].
Fitch and Smith
[8]
studied sensitivity of alignments to the weighting
functions. The example they used was taken from chicken hemoglobin
mRNA sequences, 57 bases from the
B
chain and 39 bases from the
a
chain.
A correct alignment is known here from analysis of many amino acid
sequences for which these mRNA sequences code.
With a mismatch weight of
1
[that is,
d(xy)
=1 if
x
#
y] and
w(k)
=
2.5+
k,
the correct alignment is found in the list of 14 optimal alignments.
Here 14 alignments are
in 0%
of
the optimum, 14 alignments in 1%, 35
alignments in 2%, 157 alignments in 38, 579 alignments
in
48, and 1317
alignments in 5%.
With a mismatch weight of
1
and
w(
k)
=
2.5
+
OSk,
the correct alignment
is not one
of
the two optimal alignments. Not until the list
of
31 alignments
within 4%
of
the optimum is examined is the correct alignment found.

186
MICHAEL
S.
WATERMAN AND THOMAS H. BYERS
TABLE
1
Computational and Storage Requirements
for
Stages
or
Columns
of
Nodes,
States
or
Rows
of
Nodes,
and
R
Decisions or Arcs/Node
~
Computations Storage
HP
O(RN+ KRN”) O(N+ KNo5+ K)
HPD without heaps
O(
RN
+
KRNo5) O(N+ KNo5+RN)
HPD with heaps
O(RK+ KNo510gR O(RN)
New algorithm
O(RN+ KRN”) O(N+ K)
Not only does this example illustrate the sensitivity of alignments to
weighting functions; it also shows the need for the new method. The problem
described here has a network of
2200
nodes and
110,OOO
arcs. Analysis by
Kth shortest path techniques is not practical.
COMPARISON OF METHODS
Table
1
summarizes the computational and storage requirements
of
the
Hoffman-Pavley
(HP))
algorithm, the Hoffman-Pavley-Dreyfus (HPD)
without heaps, HPD with heaps, and the new algorithm. For comparative
purposes only, the requirements are given for a square, acylic network of
N
nodes and
RN
arcs, where the average number of arcs emanating from each
node is denoted by
R
and each path contains nodes. Columns and rows
of
nodes can be viewed
as
dynamic programming stages and states, respec-
tively. The set of paths within the specified percentage of the optimal length
has exactly
K
members.
Computational requirements are estimates of the number of additions and
comparisons necessary to find the K shortest paths. Storage requirements are
estimates
of
the number of computer words needed, not including storage of
the network itself.
Each estimate of computation appearing in Table
1
contains a term
RN
for computing the original node labels. As suggested by Dreyfus (personal
communication), the published estimates for HPD in Fox
[ll]
have been
revised for the special case of a specified origin and destination. Only the
nodes along each of the K near-optimal paths are updated during each
iteration.
As
K
becomes large, the heaps allow the algorithm to become more
efficient than HP and HPD without heaps.
In estimating the new algorithm’s requirements, a worst case situation has
been assumed-none
of
the
K
paths use the same beginning arc. The
K
paths leave node
1
in K distinct directions, requiring the search to continue
for
all
nodes
of
each path.
This
situation occurs in the simple path

DYNAMIC PROGRAMMING ALGORITHM
187
problem of the previous section, but is unlikely to occur in most networks. If
some of the
K
paths begin on the same arc or set or arcs, the requirements
for the new algorithm are considerably less. Even in the worst case, the new
algorithm remains computationally competitive to HPD with heaps and at
least
as
good
as
HP and HPD without heaps.
The new algorithm requires significantly less storage than HP or either
implementation of HPD. HP must store the original node labels, an ordered
list of unused deviations, and the actual
K
paths (each of length
No
5).
HPD
without heaps must store a set of arc labels, the original node labels, and any
additional node labels along each path of
NO5
nodes. HPD with heaps must
store the arc labels and
a
heap of size
R
at each node
N.
The new algorithm stores the original node labels and may require a stack
of height
K.
The stack could become as large
as
the product of the average
number of arcs in a path and the average number of arcs emanating from a
node.
This
maximum height would only occur if K is greater than this
product, a situation which is highly unlikely. For reasonable K, the stack
length is neghgible in comparison with storing the original node labels. In
addition, since some near-optimal paths usually share beginning arcs, the
requirements are considerably less. The key feature of the new algorithm
remains its minimal storage requirements.
CONCLUSION
-
The new algorithm is easy to understand and install, which increases the
likelihood of successful implementation and subsequent user acceptance.
Only the backtracking or traceback procedure of a previously installed
shortest path problem need be modified, leaving the major component of the
model unaffected.
As
described in the introduction, Kth best path methods
are inadequate to solve most practical problems, while the new technique is
practical for many of these problems.
Although the set of near-optimal solutions can be very large, it may
contain information that is
of
interest. Frequently, the algorithm gives a
sequence of paths where the (structural) differences between adjacent paths is
small. In this situation, only every Mth path, say, need output to the user. In
some situations, it will be possible to only produce every Mth path and
reduce the running time accordingly. These problems can only be resolved in
specific cases by careful consideration of the dynamic programming problem
and the corresponding space of near-optimal solutions.
REFERENCES
1
2
R. Bellman and R. Kalaba,
On
Kth best policies,
J.
SlAM
8:582-588
(1960).
T. H. Byers and M.
S.
Waterman, Determining all optimal and near optimal solutions
when solving shortest path problems by dynamic programming,
Oper.
Res.
32
:
1381
-
1384 (1984).

188
MICHAEL
S.
WATERMAN AND THOMAS H. BYERS
3
E.
Denardo,
Dynamic Programming: Models und Applications,
Prentice-Hall, En-
glewood Cliffs, N.J.,
1980.
4
S.
Dreyfus, Appraisal
of
some shortest path algorithms,
Oper. Res.
17:395-412 (1969).
5
S.
Dreyfus and A. Law,
The Art und Theoty of Dynamic Progrumming,
Academic, New
York,
1976.
6
S.
Elmaghraby,
Some Network Models in Munagement Science,
Lecture Notes in
Economic and Mathematical Systems
29,
Springer, New York,
1970.
7
L. Fan and
C.
Wang,
The Discrete Maximum Principle,
Wiley, New York,
1964.
8
W. M. Fitch and
T.
F.
Smith, Optimal sequence alignments,
Proc. Nur. Acud.
Sci.
9 B.
Fox, Calculating Kth shortest paths,
INFOR-Cunud.
J.
Oper. Res. Inform.
-
U.S.
A,,
80~1382-1386 (1983).
Process.
11:66-70 (1973).
10
B.
Fox, More on the Kth shortest paths,
Comm. ACM
18:279 (1973).
11
B. Fox, Data structures and computer science techniques in operations research,
Oper.
Res.
26:686-717 (1978).
12
W. Hoffman and R. Pavley, Method
of
solution to Nth best path problem,
J.
Assoc.
Compur. Much.
6:506-514 (1959).
13
E. Lawler,
Combinatorial Oprimizution: Networks and Mutroids,
Holt, Rinehart, and
Winston, New York,
1976.
14
E. Minieka and D. Shier, A note on an algebra for the
K
best routes in a network,
J.
Inst. Math. Appl.
11:145-149 (1973).
15
S.
B.
Needleman and C. D. Wunsch, A general method applicable to the search for
similarities in the amino acid sequences
of
two proteins,
J.
Mol. Biol.
48444-453
(1970).
16
M. Pollack, the Kth best route through
a
network,
Oper. Res.
9:578-580 (1961).
17
M. Pollack, Solutions of the Kth best route through
a
network-a review,
J.
Math.
And. Appl.
3:547-549 (1961).
18
D. Shier, Computational experience with an algorithm for finding the Kth shortest
paths in a network,
J.
Res. Nat. Bur. Standurdr
78B:139-165 (1974).
19
D. Shier, Iterative methods for determining Kth shortest paths in network,
Networks
20
T.
F.
Smith,
M.
S.
Waterman, and W. M. Fitch, Comparative biosequence metrics,
21
M.
S.
Waterman, Sequence alignments in the neighborhood
of
the optimum with
general application to dynamic programming,
Proc. Nurl. Acud.
Sci.
U.S.
A.
22
M.
S.
Waterman, General methods
of
sequence comparison,
Bull. Muth. Biol.
23
J.
Yen, On Elmaghraby’s “The Theory of Networks and Management Science,”
Math.
Surveys
18:84-86 (1972).
6:205-229 (1976).
J.
Mol. Ed.
18~38-46 (1981).
88~3123-3124 (1983).
46:473-500 (1984).
