
Alternation and Redundancy Analysis
of the Intersection Problem
J
´
ER
´
EMY BARBAY (*)
University of Waterloo
and
CLAIRE KENYON (**)
Brown University
The intersection of sorted arrays problem has applications in search engines such as Google.
Previous work propose and compare deterministic algorithms for this problem, in an adaptive
analysis based on the encoding size of a certificate of the result (cost analysis). We define the
alternation analysis, based on the non-deterministic complexity of an instance. In this analysis we
prove that there is a deterministic algorithm asymptotically performing as well as any randomized
algorithm in the comparison model. We define the redundancy analysis, based on a measure of
the internal redundancy of the instance. In this analysis we prove that any algorithm optimal
in the redundancy analysis is optimal in the alternation analysis, but that there is a randomized
algorithm which performs strictly better than any deterministic algorithm in the comparison
model. Finally, we describe how those results can be extended b eyond the comparison model.
Keywords: randomized algorithm, intersection of sorted arrays, alternation and redundancy
adaptive analysis.
Categories and Subject Descriptors: F.2.2 [Analysis of Algorithms and Problem Complexity]:
Nonnumerical Algorithms and Problems—Sorting and searching; H.3.3 [Information Storage
and Retrieval]: Information Search and Retrieval—Search process
General Terms: Algorithms, Theory
Additional Key Words and Phrases: Adaptive Analysis, Alternation Analysis, Intersection, Redundancy
Analysis
1. INTRODUCTION
We consider search engines where queries ar e composed of several keywords, each
one b e ing associated with a sorted array of references to entries in some data base [Witten
et al. 1994, p. 136]. The answer to a conjunctive query is the intersection of the
sorted arrays corresponding to each keyword. Most search engines implement these
queries. The algor ithms are in the comparison model, where comparisons are the
only operations permitted on references.
There is an extensive literature on the merging [Hwang and Lin 1971; 1 972;
(*) School of Computer Science, University of Waterloo, Waterloo, Ontario N2L 3G1 Canada
(**) Computer Science Department, Brown University, Providence, RI 02912, United States
Permission to make digital/hard copy of all or part of this material without fee for personal
or classroom use provided that the copies are not made or distributed for profit or commercial
advantage, the ACM copyright/server notice, the title of the publication, and its date appear, and
notice is given that copying is by permission of the ACM, Inc. To copy otherwise, to republish,
to post on servers, or to redistribute to lists requires prior specific permission and/or a fee.
c
2006 ACM 0000-0000/2006/0000-0001 $5.00
ACM Journal Name, Vol. V, No. N, October 2006, Pages 1–18.
2 · J. Barbay and C. Kenyon
Christen 1978; Manacher 1979; de la Vega et al. 1993; de la Vega et al. 1998]
or intersection [Baeza-Yates 2004] of two sorted arrays. The two problems are
similar, as both re quire the algorithm to place each element in the context of the
other elements. In relational data bases, the intersection of more than two arrays is
computed by intersec ting the arrays two by two. The only optimization available
in this context consist in choosing the order in which those se ts are intersected,
and the literature explore s how to use statistics precomputed on the content of the
database to choose the best order [Chaudhuri 1998, and its references].
Demaine et al. [2001] showed that a holis tic algorithm, which considers the query
as a whole rather than as a decomposition of it in smaller two-by-two intersection
queries, is more efficient, both in theory and in practice.
In this paper we present another theoretical analysis, called the alternation
analysis [B arbay and Kenyon 2002], ba sed on the non-deterministic complexity of
the instance, and prove tight bounds on the randomized computational complexity
of the intersection. One intriguing fact of this analysis is that the lower bound apply
to randomized algorithms, whereas a deterministic algorithm is optimal. Does it
mean that no randomized algorithm can perform better than a deterministic o ne
on the intersection problem ? To answer this question, we extend the alternation
analysis to the redundancy ana lysis [Ba rbay 2003], based o n a measure of the
internal redundancy of the instance. This analysis permits to prove that fo r the
intersection problem, randomized algorithms perform better than deterministic
algorithms in term of the number of comparisons.
The redundancy analysis also makes more natur al assumptions on the instances:
the worst case in the a lternation a nalysis is such that an element considered by
the algo rithm is matched by almost all of the keywords, while in the r e dundancy
analysis the maximum number of keywords matching such an element is parameterized
by the measure of difficulty.
We define formally the interse ction problem in Section 2, and sketch the alternation
analysis and its results in Section 3. We define the redundancy analysis and study
it in Section 4: we give and analyze a randomized algor ithm in Section 4.1, and we
prove that this algorithm is optimal in Sec tion 4.2.
We ans wer the question of the usefulness o f randomized algorithms for the intersection
problem in Section 5: no deterministic algorithm can be optimal in the redundancy
analysis, hence the superiority of randomized algorithms. We list in Section 6
several perspectives of this work.
2. DEFINITIONS
We consider queries composed of several keywords, each associated to a sorted array
of references. The references can be for ins tance addresses of web pages, the only
requirement being a total order on them, i.e. that all unequal pairs of references can
be ordered. To study the intersection problem, we consider any set of two arrays
or more, of elements from a totally o rdered space, to form an insta nce . To perfo rm
any complexity analysis on such instances, we nee d to define a measure representing
the size of the instance. We define for this the signature of an instance .
Definition 2.1. We consider U to be a totally o rdered space. An instance is
composed of k sorted arrays A
1
, . . . , A
k
of positive sizes n
1
, . . . , n
k
and composed
ACM Journal Name, Vol. V, No. N, October 2006.

Alternation and Redundancy Analysis of the Intersection Problem · 3
A = 9
B = 1 2 9 11
C = 3 9 12 13
D = 9 14 15 16
E = 4 10 17 18
F = 5 6 7 10
G = 8 10 19 20
A : 9
B : 1 2 9 11
C : 3 9 12 13
D : 9 14 15 16
E : 4 10 17 18
F : 5 6 7 10
G : 8 10 19 20
Fig. 1. An instance of the intersection problem: on the left is the array representation of the
instance, on the right is a representation which expresses i n a better way the structure of the
instance, where the x-coordinate of each element is equal to its value.
of elements from U. The signature of such an instance is (k, n
1
, . . . , n
k
). An instance
is “of s ignature at m ost” (k, n
1
, . . . , n
k
) if it can be completed by adding arrays and
elements to form an instance of signature exactly (k, n
1
, . . . , n
k
).
Example 2.2. Consider the instance of Figure 1 , where the ordered space is the
set of positive integers: it has signature (7, 1, 4, 4, 4, 4, 4, 4)
Definition 2.3. The Intersection of an instance is the set A
1
∩ . . . ∩ A
k
composed
of the elements that are present in k distinct arrays.
Example 2.4. The intersection A ∩ B ∩ . . . ∩ G of the instance of Figure 1 is
empty, as no element is present in more than 4 arrays.
Any algorithm (even a non-deterministic one) computing the intersection must
prove the correctness of the output: first, it must certify that all the elements of
the output are indeed elements of the k arrays; second, it must certify that no
element of the intersection has been omitted, by exhibiting some certificate that
there can be no other elements in the intersection than those output. We define
the partition-certificate as such a proof.
Definition 2.5. A partition-certificate is a partition (I
j
)
j≤δ
of U into intervals
such that any singleton {x} corresponds to an element x of ∩
i
A
i
, and each other
interval I has an empty intersec tion I ∩ A
i
with at least one array A
i
.
3. ALTERNATION ANALYSIS
Imagine a function which indicates for each element x ∈ U the name of an ar ray
not containing x if x is not in the intersection, and “all” if x is in the intersection.
The minimal number of times such a function alternates names, for x sca nning U
in increasing order, is just one less than the minimal size of a partition-certificate
of the instance, which is called the alternation of the instance.
Definition 3.1. The alternation δ of an instance (A
1
, . . . , A
k
) is the minimal
number of intervals forming a partition-certificate of this instance.
Example 3.2. The alternation of the instance in Figure 1 is δ=3, as we can see on
the right re presentation that the partition (−∞, 9), [9, 10), [10, +∞) is a partition-
certificate of size 3, and that none can be smaller.
The alternation of an instance I is als o the complexity o f the best non-deterministic
algorithm on I (plus 1 ), i.e. the non-deterministic complexity. This non-deterministic
ACM Journal Name, Vol. V, No. N, October 2006.

4 · J. Barbay and C. Kenyon
complexity forms a weak lower bound on the complexity of any randomized or
deterministic algorithm solving I, and hence a natural measure of the difficulty of
the instance.
Indeed, among instances of same signature and alternation, it is possible to
prove a tight bound on the randomized complexity of the intersection problem:
by providing a difficult distribution of ins tances a nd using the minimax principle,
we prove a lower bound on the complexity of any randomized algorithm solving the
problem [Barbay a nd Kenyon 2002].
Theorem 3.3 Alternation Lower Bound [Barbay and Kenyon 2002].
For any k≥2, 0<n
1
≤ . . . ≤n
k
and δ∈{4, . . . , 4n
1
}, and for any randomized algorithm
A
R
for the intersection problem, there is an instance of signature at most (k, n
1
, . . . , n
k
)
and alternation at most δ, such that A
R
performs Ω(δ
P
k
i=1
log(n
i
/δ)) comparisons
on average on it.
Proof. This is a simple application of Lemma 4.9 (stated and proved in Section 4.2)
and of the Yao-von Neumann principle [Neumann and Morgenstern 1944 ; Sion 1958;
Yao 1977]:
—Lemma 4.9 gives a distribution for δ ∈ {4, . . . , 4n
1
} on instances of alternation
at most δ,
—Then the Yao-von Neumann principle permits to deduce from this distr ibution a
lower bound on the worst case complexity of randomized algorithms.
On the other hand, a simple deterministic algorithm reaches this lower bound.
As the class of deterministic algorithms is co ntained in the c lass of randomized
algorithms, this proves that the bound is tight for randomized algorithms.
Theorem 3.4 Alternation Upper Bound [Barbay and Kenyon 2002].
There is a deterministic algorithm which performs O(δ
P
k
i=1
log(n
i
/δ)) comparisons
on any instance of signature (k, n
1
, . . . , n
k
) and alternation δ.
Proof. The deterministic version of Algorithm Rand Intersection (see Section 4.1),
where the choice of a random arr ay is replaced by the choice of the next array in a
fixed order, performs O(δ
P
k
i=1
log(n
i
/δ)) comparisons on an instance of signature
(k, n
1
, . . . , n
k
) and of alternation δ. Its analysis is very simila r to the one of the
randomized version given in the proof of Theorem 4.7.
Note that this algorithm is distinct from the algo rithm presented previously [Barbay
and Kenyon 2002], wher e the a lgorithm was p e rforming unbounded searches in
parallel in the arrays. Here the algorithm performs one unbounded search at a
time, which saves some compa risons in many cases, for any arbitr ary signature
(k, n
1
, . . . , n
k
) (but not in the worst case).
The lower bound apply to any randomized algor ithm, when a mere deterministic
algorithm is optimal. Do es it mean that no randomized algorithms can do better
than a deterministic one on the intersection problem? We refine the analys is to
answer this question.
4. REDUNDANCY ANALYSIS
By definition of the partition-c e rtificate:
ACM Journal Name, Vol. V, No. N, October 2006.
Alternation and Redundancy Analysis of the Intersection Problem · 5
—for each singleton {x} of the partition, any algorithm must find the position of
x in all arrays A
i
, which takes k searches;
—for each interval I
j
of the partition, any algorithm must find an array, or a s e t of
arrays, s uch that the intersection o f I
j
with this array, or with the intersection
of those arr ays, is empty.
The cost for finding such a set of arrays can vary, and depends on the choices
performed by the algorithm. In general, it requires fewer searches if there are many
possible answers. To take this into account, for each interval I
j
of the par tition-
certificate we will count the number r
j
of arrays whose intersection with I
j
is empty.
The smaller is r
j
, the har der is the instance: 1/r
j
measures the contribution of this
interval to the difficulty of the instance.
Example 4.1. Consider for instance the interval I
j
= [10, 11) in the instance
of Figure 1: r
j
= 4 arrays have an empty intersection with it. A randomized
algorithm, choosing an array uniformly at random, has probability r
j
/k to find an
array which does not intersect I
j
, and will do so after at most ⌈k/r
j
⌉ trials on
avera ge, even if it tries several times in the same array because it doesn’t memorize
which array it tried before . As the number of arrays k is fixed, the value 1/r
j
measures the difficulty of proving that no element of I
j
is in the intersection of the
instance.
We name the sum of those contributions the redundancy of the instance, and it
forms our new measure of difficulty:
Definition 4.2. Let A
1
, . . . , A
k
be k sorted arrays, and let (I
j
)
j≤δ
be a partition-
certificate for this instance.
—The redundancy ρ(I) of an interval or singleton I is defined as equal to 1 if I is
a singleton, and equal to 1/#{i, A
i
∩ I = ∅} otherwise.
—The redundancy ρ((I
j
)
j≤δ
) of a partition-certificate (I
j
)
j≤δ
is the sum
P
j
ρ(I
j
)
of the redundancies of the intervals composing it.
—The redundancy ρ ((A
i
)
i≤k
) of an instance of the intersection problem is the
minimal redundancy min{ρ ((I
j
)
j≤δ
) , ∀(I
j
)
j≤δ
} of a partition-certificate of the
instance.
Note that the redundancy is always well defined and finite: if I is not a singleton
then by definition there is at least o ne array A
i
whose intersection with I is empty,
hence #{i, A
i
∩ I = ∅} > 0.
Example 4.3. The partition-certificate {(−∞, 9), [9, 10), [10 , 11), [11, +∞)} has
redundancy at most 1/2+1/3+1/4+1/2 = 7/6 for the instance given Figure 1,
and no other partition-certificate has a smaller re dundancy, hence the instance has
redundancy 7/6.
The main idea is that the redundancy analysis permits to measure the difficulty
of the instance in a finer way than the alternation analysis: for fixed k, n
1
, . . . , n
k
and δ, several instances of signa tur e (k, n
1
, . . . , n
k
) and alternation δ may present
various levels of difficulty, and the redundancy helps to distinguish between those.
ACM Journal Name, Vol. V, No. N, October 2006.
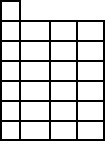
6 · J. Barbay and C. Kenyon
A = 9
B = 1 2 9 11
C = 3 9 12 13
D = 9 14 15 16
E = 4 10 17 18
F = 5 6 7 9
G = 8 9 19 20
A : 9
B : 1 2 9 11
C : 3 9 12 13
D : 9 14 15 16
E : 4 10 17 18
F : 5 6 7 9
G : 8 9 19 20
Fig. 2. A much more difficult variant of the instance of Figure 1: only two elements changed,
F [4] and G[2] whi ch were equal to 10 and are now equal to 9, but the redundancy is now ρ =
1/2+1+1/6+1/2 = 2+1/6.
Example 4.4. In the instance from Figure 1, the only way to prove the e mptiness
of the intersection is to co mpute the intersection of one of the arrays chosen from
{A, B, C, D} with one of the ar rays chosen fro m {E, F, G}, beca use 9 ∈ A∩B∩C∩D
and 10 ∈ E ∩ F ∩ G. For simplicity, and without lo ss of generality, suppose that
the algorithm searches to intersect A with another array in {B, C, D, E, F, G},
and consider the number of unbounded searches performed, instead of the number
of comparisons. The randomized algorithm looking for the element of A in a
random a rray from {B, C, D, E, F, G} performs on avera ge only 2 searches, as the
probability to find an array whose intersection is empty with A is then 1/2.
On the o ther hand, consider the instance of Figure 2, a variant of the instance of
Figure 1, where element 9 is present in all the arrays but E. As the two instances
have the same signature and alterna tio n, the alternation analysis yields the same
lower bound for both instances. But the randomized algorithm described above now
performs on average k/2 searches, as oppo sed to 2 searches on the original instance.
This difference in difficulty, between those very similar instances, is not expressed
by a difference of alternation, but it is expressed by a difference of redundancy:
the new instance has a redundancy of 1/2+1+1/6+1/2 = 2+1/6, which is larger
by one than the redundancy 7/6 of the original instance . This difference of one
corresponds to k more doubling searches for this simple instance. This difference
is used in Section 5 to crea te instances where a deterministic algorithm performs
O(k) times more searches and comparisons than a randomized algorithm.
4.1 Randomized algorithm
For simplicity, we ass ume that all a rrays contain the e lement −∞ at position 0
and the element +∞ at position n
i
+1. Given this convention, the intersection
algorithm can ignore the sizes of the sets. This is the case in particular in pipe-lined
computations, wher e the sets are not completely computed when the intersection
starts, for instance in parallel applications.
An unbounded search lo oks for an element x in a sorted array A of unknown
size, starting at position init. It returns a value p such that A[p−1]<x≤A[p], called
the insertion rank of x in A. It can be perfo rmed combining the doubling search
and binary search algorithms [Barbay and Kenyon 2002; Demaine et al. 2000; 2001],
and is then of complexity 2⌈log
2
(p−init)⌉, o r in a more complicated way [Bentley
and Yao 19 76] to improve the complexity by a c onstant factor of less than 2.
Using unbounded search rather than binary search is crucial to the complexity
ACM Journal Name, Vol. V, No. N, October 2006.

Alternation and Redundancy Analysis of the Intersection Problem · 7
Algorithm Rand Intersection (A
1
, . . . , A
k
)
for all i do p
i
← 1 end for
Result ← ∅; s ← 1
repeat
m ← A
s
[p
s
]
#NO ← 0; #YES ← 1;
while YES < k and #NO = 0
Let A
s
be a random array s.t. A
s
[p
s
] 6= m.
p
s
← Unbounded Search(m, A
s
, p
s
)
if A
s
[p
s
] 6= m then #NO ← 1 else #YES ← YES + 1 end if
endwhile
if #YES = k then Result ← Result ∪ {m} end if
for all i such that A
i
[p
i
] = m do p
i
← p
i
+ 1 end for
until m = +∞
return Result
Fig. 3. The algorithm Rand Intersection: Given k non-empty sorted sets A
1
, . . . , A
k
of sizes
n
1
, . . . , n
k
, the al gorithm computes in variable Result the intersection A
1
∩ . . . ∩ A
k
. Note that
the only random instruction is the choice of the array in the inner loop.
of the intersection algorithm. Consider the task of searching d e lements x
1
≤ x
2
≤
. . . ≤ x
d
in a sorted array of size n. It requires d log n
i
comparisons using binary
search, but less than 2d log(n
i
/d) comparisons using unbounded search. To see
that, define p
j
such that p
0
= 0 and A[p
j
] = x
j
∀j ∈ {1, . . . , d}: the jth doubling
search performs, no more than 2 log(p
j
− p
j−1
) comparisons. By co ncavity of the
log, the sums
P
j≤d
2 log(p
j
− p
j−1
) is no larger than 2d log(
P
j≤d
(p
j
− p
j−1
)/d).
The sum
P
j≤d
(p
j
−p
j−1
) is equa l to p
d
−p
0
, which is smaller than the size n of the
array. Hence the d doubling searches perform less than 2d log(n
i
/d) comparisons.
Theorem 4.5. Algorithm Rand Intersection (see Fig. 3) computes the intersection
of the arrays given as input.
Proof. Given k non-empty sorted sets A
1
, . . . , A
k
of sizes n
1
, . . . , n
k
, the Rand
Intersection algorithm (Fig. 3) c omputes the intersection A
1
∩ . . . ∩A
k
. The
algorithm is composed of two nested loops. The outer loop iterates through potential
elements of the intersection in variable m and in increasing order, and the inner
loop checks for each value of m if it is in the intersection.
In each pass of the inner loop, the algorithm searches for m in one array A
s
which potentially contains it. The invariant of the inner loop is that, at the start of
each pass and for each arr ay A
i
, p
i
denotes the first potential position for m in A
i
:
A
i
[p
i
− 1] < m. The varia bles #YES and #NO count how many arrays are known
to contain m, a nd are updated depending on the result of each search.
A new value for m is chosen every time we enter the outer loop, at which time the
current subproblem is to compute the inter section on the sub-arrays A
i
[p
i
, . . . , n
i
]
for all values of i. Any first element A
i
[p
i
] of a sub-array could be a candidate, but
a better c andidate is one which is lar ger than the last value of m: the algorithm
chooses A
s
[p
s
], which is by definition larger than m. Then only one array A
s
is
known to contain m, hence #YES ← 1, and no array is known n ot to contain it,
hence #NO ← 0. The algorithm terminates when all the values of the current array
have been considered, and m has taken the last value + ∞.
ACM Journal Name, Vol. V, No. N, October 2006.
8 · J. Barbay and C. Kenyon
We now analyze the complexity of Algorithm Rand Intersection (Fig. 3) as a
function of the redundancy ρ of the instance. To understand the intuition behind
the analysis, consider the following example:
Example 4.6. For a fixed interval I
j
, suppose that the algorithm rece ives six
arrays such that A
1
, A
2
, A
3
and A
4
contain many elements from I
j
but have none
in common, and such that A
5
and A
6
contain no elements from I
j
. Ignore all steps
of the algorithm where m takes values out of the interval I
j
: the interval defines
a phase of the algorithm. Suppose that m takes a value in I
j
at some point, for
instance from A
1
. At each iteration of the external loop, the algorithm ignores
the array from which the current value of m was taken, chooses one between the
four remaining arrays, searches in the chosen one, and updates the value of m
accordingly.
—With probability 3/5 the algorithm chooses the set A
1
, A
2
, A
3
or A
4
(depending
of which set the current value of m comes from) and potentially fails to terminate
the phase.
—With probability 2/5 the algorithm chooses A
5
or A
6
, performs a sea rch in it
(there might be elements left from intervals I
1
∪ . . . ∪ I
j−1
), and updates m to a
value from I
j+1
, which terminates the current phase.
We are interested in the number C
j
i
of searches performed in each array A
i
during
this phase. As m takes a value outside of I
j
after a sea rch in A
5
or A
6
, C
j
5
and C
j
6
are random boolean variables, which depend only on the las t choice of the algorithm
befo re changing phas e : the expectation of C
j
5
(resp. C
j
6
) is exactly the probability
that A
5
(resp. A
6
) is picked knowing that one of those is picked, i.e. 1/2.
The algorithm can perfor m many sear ches in A
1
, A
2
, A
3
and A
4
, so the variables
C
j
1
, C
j
2
, C
j
3
and C
j
4
are r andom integer variables, which depend on all the choices
of the algorithm but the last. The proba bility that A
1
is chosen is null if m comes
from A
1
. Otherwise it is less than the probability that A
1
is chosen knowing that
m does n’t come from A
1
: Pr[A
1
is chosen ] = Pr[A
1
is chosen and m does not come
from A
1
] ≤ Pr[A
1
is chosen |m does not come from A
1
]. Hence the probability that
A
1
is chosen is less than 1/4.
C
j
1
is increased each time A
1
is chosen (probability a ≤ 1/5), is finalized as s oon
as A
5
or A
6
is chosen (probability b = 2/5), and stays the same each time another
array is chosen (probability c ≥ 2/5). Ignore all the steps where C
j
2
, C
j
3
or C
j
4
are
increased: knowing that C
j
2
, C
j
3
or C
j
4
are not increased, the probability that C
j
1
is
increased is a/(a+b) ≤ 1/3, and the probability that it is finalized is b/(a+b) ≥ 2/3.
Such a system will iterate a t most 3/2 times on average, and increment C
j
1
each
time but the last, i.e. 3/2 − 1 = 1/2 times on average. The same reasoning holds
for A
2
, A
3
and A
4
. Hence in this example E(C
j
i
) = 1/2 for each set A
i
, where 2 is
the numb e r of arrays which contain no elements from I
j
.
The proof of Theorem 4.7 argues similarly in the more general case.
Theorem 4.7 Redundancy Upper Bound [Barbay 2003]. Algorithm Rand
Intersection (Fig. 3) performs on average O(ρ
P
k
i=1
log(n
i
/ρ)) comparisons on
any instance of signature (k, n
1
, . . . , n
k
) and of redundancy ρ.
ACM Journal Name, Vol. V, No. N, October 2006.

Alternation and Redundancy Analysis of the Intersection Problem · 9
Proof. Let (I
j
)
j≤δ
be a partition-certificate of minimal redundancy ρ. Each
comparison perfor med by the algorithm is said to be performed in phase j if m ∈ I
j
for some interval I
j
of the partition. Let C
j
i
be the number of searches performed
by the algorithm during phase j in array A
i
, let C
i
=
P
j
C
j
i
be the number of
searches performed by the algorithm in array A
i
over the whole execution, and let
(r
j
)
j≤δ
be such that r
j
is equal to 1 if I
j
is a singleton, and to #{i, A
i
∩ I
j
= ∅}
otherwise.
Let us consider a fixed phase j ∈ {1, . . . , δ}, and compute the average number
of searches E(C
j
i
) performed in each array A
i
during phase j. At each iteration
of the internal loop, the algorithm chooses an a rray in which m is not known to
be. As m always comes from one array, there are at most k − 1 of those arrays,
hence each array is chosen with probability at least 1/(k − 1). If the element m
currently considered is in the intersection, then each arr ay A
i
will be searched and
C
j
i
is equal to 1. In this case 1/r
j
is also equal to 1, so that C
j
i
=1/r
j
=E(C
j
i
).
Suppose that m is not in the intersection, and that A
i
∩ I
j
is empty. Either A
i
is never chosen, and C
j
i
= 0; or A
i
is chosen, and C
j
i
= 1, because the algorithm
will terminate the phase after searching in A
i
. The probability that A
i
is chosen is
at most the probability that it is chos en knowing tha t this is the last search of the
phase:
Pr[A
i
is chosen] = Pr[A
i
is chosen and last search] ≤ Pr[A
i
is chosen| last search].
As the arrays are chosen uniformly, this proba bility is Pr{C
j
i
= 1} ≤ 1/r
j
, and
the average number of searches is at most E(C
j
i
) = 1 ∗ Pr{C
j
i
= 1} ≤ 1/r
j
.
The interesting c ase is when m is not in the intersection but A
i
∩ I
j
6= ∅. At each
new search, either
(1) C
j
i
is incremented by one because the search occur red in A
i
, which occurs with
probability less than 1/(k − 1);
(2) or C
j
i
is fixe d in a final way beca us e an array was found which intersection with
I
j
is empty, which occurs with probability r
j
/(k − 1);
(3) or C
j
i
is neither incremented nor fixed, if another array was se arched but its
intersection with I
j
is not empty.
The co mbined probability of the first and second case is 1/(k − 1) + r
j
/(k − 1).
Ignoring the third case where C
j
i
never changes, the c onditional probability of
the first case is
1
k−1
/(
1
k−1
+
r
j
k−1
). Hence this system is equivalent to a system
where C
j
i
is incremented by one with probability at least 1/(1 + r
j
), and fixed with
the remaining probability, at most r
j
/(1 + r
j
). Such a system iterates at most
(1 + r
j
)/r
j
times on average, a nd increments C
j
i
at e ach iteration but the last: the
final value of C
j
i
is at most (1 + r
j
)/r
j
− 1 = 1/r
j
.
Hence the average number of searches performed in each array A
i
during phase j
is E(C
j
i
) ≤ 1/r
j
. Summing over all phas e s, it implies that the algorithm performs
on avera ge E(C
i
) ≤
P
j
1/r
j
= ρ searches in each array A
i
.
Let g
ℓ
i,j
be the increment of p
i
due to the ℓth unbounded search in array A
i
during
phase j. Notice that
P
j,ℓ
g
ℓ
i,j
≤ n
i
. The algorithm performs at most 2 log(g
ℓ
i,j
+ 1)
comparisons during the ℓth search of phase j in array A
i
. So it performs at most
ACM Journal Name, Vol. V, No. N, October 2006.

10 · J. Barbay and C. Kenyon
2
P
j,ℓ
log(g
ℓ
i,j
+ 1) comparisons between m and an element of array A
i
during the
whole execution. Because of the concavity of the function log(x+ 1), this is sma ller
than 2C
i
log(
P
j,ℓ
g
ℓ
i,j
/C
i
+1), and beca use of the preceding remark
P
j,ℓ
g
ℓ
i,j
≤n
i
,
this is smaller than 2C
i
log(n
i
/C
i
+ 1).
The functions f
i
(x)=2x log(n
i
/x+1) are concave for x≤n
i
, so E(f
i
(C
i
))≤f
i
(E(C
i
)).
As the average complexity of the algorithm in array A
i
is E(f(C
i
)), and as E(C
i
) =
ρ, on average the algorithm performs less than 2ρ log(n
i
/ρ+1) comparisons between
m and an element in array A
i
. Summing over i we get the final result, which is
O(ρ
P
i
log n
i
/ρ).
4.2 Randomized Complexity Lowe r Bound
We prove now that no rando mized algorithm can do asymptotically better in
(k, n
1
, . . . , n
k
). The proof is quite similar to the lower bound of the alternation
analysis [B arbay and Kenyon 2002], and differs mostly in Lemma 4.8, which must
be adapted to the redundancy.
The Lemma s 4.8 and 4.9 are used to prove the alternation lower bound in
Theorem 3.3 and to prove the redundancy lower bound in T heorem 4.10.
In Lemma 4.8 we prove a lower bound on average on a distribution of ins tances
of alternation and redundancy at most ρ = 4 and of intersection s ize at most 1. We
use this result in Lemma 4.9 to define a distribution on instances of alternation and
redundancy at most ρ ∈ {4, 4n
1
} by c ombining p = θ(ρ) sub- ins tances. Applying
the Yao-von Neumann principle [Neumann and Morg e nstern 1 944; Sion 1958; Yao
1977] in Theore m 4.10 gives us a lower bound of Ω(ρ
P
k
i=2
log(n
i
/ρ)) on the
complexity of any randomized algorithm for the intersection problem.
Finally in Lemma 4.11, we prove that any instance of signature (k, n
1
, . . . , n
k
)
has redundancy ρ at most 2n
1
+1, so that the redundancy analysis of Theorem 4.10
covers totally all instances for a given signature (k, n
1
, . . . , n
k
).
Lemma 4.8 . For any k ≥ 2, 0<n
1
≤ . . . ≤n
k
, there is a distribution on instances
of the intersection problem with signature at most (k, n
1
, . . . , n
k
), alternation and
redundancy at most 4, such that any deterministic algorithm performs at least
(1/4)
P
k
i=2
log(2n
i
+ 1) +
P
k
i=2
1/(2n
i
+1) − k+2 comparisons on average.
Proof. Let C be the total number of comparisons performed by the algorithm,
and for each array A
i
note F
i
= log
2
(2n
i
+ 1), and F =
P
k
i=2
F
i
.
Let us draw an index w ∈ {2, . . . , k} equal to i with probability F
i
/F , and
(k − 1) positions (p
i
)
i∈{2,...,k}
such that ∀i each p
i
is cho sen uniformly at random
in {1, . . . , n
i
}. Let P and N be two instances such that in both P and N, for
any 1<i<j≤k, a∈A
1
, b, c∈A
i
and d, e∈A
j
then b<A
i
[p
i
]<c and d< A
j
[p
j
]<e imply
b<d<a<c<e (see Figure 4); in P , A
w
[p
w
]=A
1
[1]; in N A
w
[p
w
]>A
1
[1]; and such
that the elements at position p
i
in all other arrays than A
w
are equal to A
1
[1].
Let x = A
1
[1] be the first element of the first array. Define x-comparisons to
be the comparisons between any element and x. Because of the special relative
positions of the elements, a compar ison between two elements b and d in a ny
arrays does not yield mo re information than the two comparisons between x and
b and between x and d: the positions of elements b and d relative to x permit
to deduce their order. Hence any algorithm performing C comparisons between
ACM Journal Name, Vol. V, No. N, October 2006.
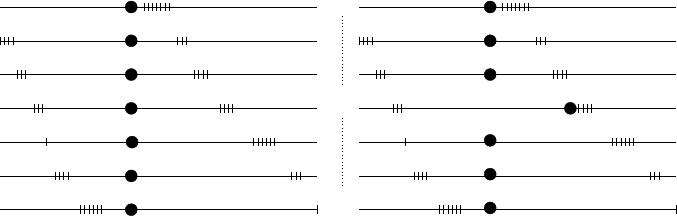
Alternation and Redundancy Analysis of the Intersection Problem · 11
b
d e
b
d e
cc
A
w
N
a
A
1
A
k
P
a
Fig. 4. Distribution on (P, N ): each element of value v is represented by a dot of x-coordinate v,
and large dots correspond to the element at position p
i
in each array A
i
.
arbitrary elements can be express e d as an algorithm performing no more than
2C x-comparisons, and any lower bo und L on the complexity of algorithms using
only x-comparisons is an L/2 lower bound on the complexity of algorithms using
comparisons between arbitrary elements.
The alternation of such instances is at most 4, and the redundancy of such
instances is no more than 3 + 1/(k −1), which is less than 4:
—the interval (−∞, A
1
[1]) is sufficient to certify that no element smaller than x is
in the intersection, and stands for a redundancy of at most 1;
—the interval (A
1
[n
1
], +∞, ) is sufficient to certify that no element larger than
A
1
[n
1
] is in the intersection, and stands for a redundancy of at most 1;
—the interval [A
1
[1], A
1
[n
1
]] is sufficient in N to complete the partition-certificate,
and stands for a redundancy of at most 1;
—the singleton {x} and the interval (A
1
[1], A
1
[n
1
]] are sufficient in P to complete
the partition-certificate, and stand for a redundancy of at most 1+1/(k − 1 ).
The only difference betwe e n instances P and N is the relative pos itio n of the
element A
w
[p
w
] to the other elements composing the instance, as described in
Figure 4. Any algorithm computing the intersection of P has to find the (k − 1)
positions {p
2
, . . . , p
k
}. Any algorithm c omputing the inte rsection of N has to
find w and the associated p osition p
w
. Any algorithm distinguishing between
P and N has to find p
w
: we will prove that it needs on average almost F/2 =
(1/2)
P
k
i=2
log
2
(2n
i
+ 1) x-comparisons to do so on a distribution corresponding to
the uniform choice between a n instance N and an instance P .
Consider a deterministic algorithm using only x-comparisons to compute the
intersection. As the algorithm has not distinguished between P and N till it found
w, let X
i
denote the number of x-co mparisons performed in a rray A
i
for both P or
N. Let Y
i
denote the number of x-comparisons performed in arr ay A
i
for N; and
let ξ
i
be the indicator var iable which equals 1 exactly if p
i
has been determined on
instance P . The number of comparisons performed is C =
P
k
i=2
X
i
. Restricting
ourselves to arr ays in which the position p
i
has been determined, we can write
C ≥
P
k
i=2
X
i
ξ
i
=
P
k
i=2
Y
i
ξ
i
.
ACM Journal Name, Vol. V, No. N, October 2006.

12 · J. Barbay and C. Kenyon
Let us consider E(Y
i
ξ
i
): the expectancy can be decomposed as a sum of probabilities
E(Y
i
ξ
i
)=
P
h
Pr{Y
i
ξ
i
≥h}, and in particular E(Y
i
ξ
i
)≥
P
F
i
h=1
Pr{Y
i
ξ
i
≥h}. Those
terms can be decomposed using the proper ty Pr{a∨b} ≤ Pr{a}+ Pr{b}:
Pr{Y
i
ξ
i
≥ h} = Pr{Y
i
≥ h ∧ ξ
i
= 1}
= 1 − Pr{Y
i
< h ∨ ξ
i
= 0}
≥ 1 − Pr{Y
i
< h} − Pr{ξ
i
= 0}
= Pr{ξ
i
= 1} − Pr{Y
i
< h} (1)
The probability Pr{Y
i
< h} is bounded by the usual decision tree lower bound:
if we consider the binary x-co mparisons performed in s e t A
i
, there are at most
2
h
leaves at depth less than h. Since the insertion rank of x in A
i
is uniformly
chosen, these leaves have the same probability and have total probability at most
Pr{Y
i
<h}≤2
h
/(2n
i
+ 1)=2
h−F
i
. Those terms for h ∈ {1, . . . , F
i
} form a geometric
sequence whose sum is equal to 2(1−2
−F
i
), so E(Y
i
ξ
i
) ≥ F
i
Pr{ξ
i
= 1}−2(1−2
−F
i
).
Then
E(C) ≥
k
X
i=2
E(Y
i
ξ
i
) ≥
k
X
i=2
F
i
Pr{ξ
i
= 1} −
k
X
i=2
2(1 − 2
−F
i
)
≥
k
X
i=2
F
i
Pr{ξ
i
= 1} + 2
k
X
i=2
2
−F
i
− 2(k − 2). (2)
Let us fix p = (p
2
, . . . , p
k
). There are only k − 1 possible choices for w. The
algorithm can only differentiate between P and N when it finds w. Let σ denote
the order in which these instances are dealt with for p fixed. Then ξ
i
= 1 if and
only if σ
i
≤ σ
w
, and so Pr{ξ
i
= 1|p} =
P
j:σ
j
≥σ
i
F
j
/F .
Summing over p, and then over i, we get an expression of the firs t term in
Equation (2):
Pr{ξ
i
= 1} =
X
p
Pr{ξ
i
= 1|p} Pr{p} =
X
p
X
j:σ
j
≥σ
i
F
j
F
Pr{p}
k
X
i=2
F
i
Pr{ξ
i
= 1} =
X
p
k
X
i=2
X
j:σ
j
≥σ
i
F
i
F
j
F
Pr{p} =
X
p
Pr{p}
k
X
i=2
X
j:σ
j
≥σ
i
F
i
F
j
F
.
In the sum, each term “F
i
F
j
” appears exactly once, and
X
i
F
i
!
2
= 2
X
i
X
i≤j
F
i
F
j
−
X
i
F
i
2
,
hence
k
X
i=2
X
j:σ
j
≥σ
i
F
i
F
j
=
1
2
k
X
i=2
F
i
!
2
+
k
X
i=2
F
i
2
,
ACM Journal Name, Vol. V, No. N, October 2006.

Alternation and Redundancy Analysis of the Intersection Problem · 13
N
p
N
1
P
2
Fig. 5. p elementary instances unified to form a single large instance.
which is independent of p. Then we can conclude:
k
X
i=2
F
i
Pr{ξ
i
= 1} =
1
2
1
F
k
X
i=2
F
i
!
2
+
k
X
i=2
F
i
2
X
p
Pr{p} =
1
2
k
X
i=2
F
i
.
Plugging this into Equation (2), we obtain a lower bound on the average number
of x-comparisons E(C) performed by any deterministic algorithm which performs
only x-comparisons, of (1/2)
P
k
i=2
F
i
+ 2
P
k
i=2
2
−F
i
− 2(k−2), w hich is equal to
(1/2)
P
k
i=2
log
2
(2n
i
+1) + 2
P
k
i=2
1/(2n
i
+1) − 2(k−2). This implies a lower bound
of (1/4 )
P
k
i=2
log
2
(2n
i
+1) +
P
k
i=2
1/(2n
i
+1) − (k−2) on the average number of
comparisons performed by any deterministic algorithm, hence the result.
Lemma 4.9 . For any k ≥ 2, 0<n
1
≤ . . . ≤n
k
and ρ∈{4, . . . , 4 n
1
}, there is a
distribution on instances of the intersection problem of signature at most (k, n
1
, . . . , n
k
),
of alternation and redundancy at most ρ, such that any deterministic algorithm
performs on average Ω(ρ
P
k
i=1
log(n
i
/ρ)) comparisons.
Proof. Let’s draw p=⌊ρ/4⌋ pairs (P
j
, N
j
)
j∈{1,...,p}
of sub-instances of signature
(k, ⌊n
1
/p⌋, . . . , ⌊n
k
/p⌋) from the distribution of Lemma 4.8. As ρ ≤ 4n
1
, p ≤ n
1
and ⌊n
1
/p⌋ > 0, the sizes of all the arrays are positive. Let’s choose uniformly at
random e ach sub-instance I
j
between the sub-instance P
j
which intersection is a
singleton and the sub-instance N
j
which intersection is empty, and form a larg e r
instance I by unifying the arrays of same index from each sub-instance, such that
the elements from two different sub-instances never interleave, as in Figure 5.
This defines a distribution on instances of alter nation and redundancy at most
ρ (a s 4p = 4⌊ρ/4⌋ ≤ ρ), and of signatur e at most (k, n
1
, . . . , n
k
). Solving this
instance implies to solve all the p sub-instances. Lemma 4.8 gives a lower bound
of (1/4)
P
k
i=2
log(2n
i
/p + 1 ) +
P
k
i=2
1/(2n
i
+1) − k+ 2 comparisons on average for
each of the p sub problems, hence a lower bound of
(p/4)
k
X
i=2
log(2n
i
/p + 1) + p
k
X
i=2
1/(2n
i
/p+1) − k+2
!
,
which is Ω(ρ
P
k
i=1
log(n
i
/ρ)).
ACM Journal Name, Vol. V, No. N, October 2006.

14 · J. Barbay and C. Kenyon
Theorem 4.10 Redundancy Lower Bound [Barbay 2003]. For any k ≥
2, 0<n
1
≤ . . . ≤n
k
and ρ ∈ {4, . . . , 4n
1
}, and for any randomized algorithm A
R
for
the int ersection problem, there is an instance of signatu re at most (k, n
1
, . . . , n
k
),
and redundancy at most ρ, such that A
R
performs Ω(ρ
P
k
i=1
log(n
i
/ρ)) comparisons
on average on it.
Proof. The proof is identical to the proof of Theorem 3.3, as the instances
generated by the proof are of alternatio n equal to their redundancy. This is a
simple application of Lemma 4.9 and of the Yao- von Neumann principle [Neumann
and Morgenstern 1944 ; Sion 1958; Yao 1977]:
—Lemma 4.9 gives a distribution for ρ ∈ {4, . . . , 4n
1
} on instances of redundancy
at most ρ,
—Then the Yao-von Neumann principle permits to deduce from this distr ibution a
lower bound on the worst case complexity of randomized algorithms.
This analys is is more prec ise than the lower bound previously presented [B arbay
and Kenyon 2002], where the additive term in −k was ignored, although it makes the
lower bound trivially negative for large values of the difficulty δ. Here the additive
term is suppressed for min
i
n
i
≥ 128, and the multiplicative factor between the
lower bound and the upper bound is reduced to 16 instead of 64. This technique
can be applied to the alternation analysis of the intersection with the same result.
Note also that a multiplicative factor of 2 in the gap comes from the unbounded
searches in the algorithm, and can be reduced using a more c omplicated algorithm
for the unbounded search [Be ntley and Yao 1976].
One could wonder how the lower b ound evolves for redundancy values larger than
4n
1
. The following result shows that no instance with such redundancy can exist.
Lemma 4.1 1. For any k ≥ 2 and 0<n
1
≤ . . . ≤n
k
, any instance of signature
(k, n
1
, . . . , n
k
) has redundancy ρ at most 2n
1
+1.
Proof. First observe that there is always a partition-certificate of size 2n
1
+ 1.
Then that the redundancy of any partition-certificate is by definition smaller than
the size of the partition. Hence the result.
Note that this does not contradict the result from Lemma 4.9, which defines a
distribution of instances of redundancy at most 4n
1
.
5. COMPARISONS BETWEEN THE ANALYSIS
The redundancy analysis is strictly finer than the alternation analysis: s ome algorithms,
optimal for the alternation analysis, are not optimal anymore in the redundancy
analysis (Theorem 5.1), and any algorithm optimal in the redundancy analys is is
optimal in the alternation analysis (Theorem 5.2). So the Rand Intersection
algorithm is theoretically better than its deterministic variant in the comparison
model, and the redundancy analysis permits a better analysis than the alternation
analysis.
Theorem 5.1. For any k ≥ 2, 0<n
1
≤ . . . ≤n
k
and ρ ∈ {4, . . . , 4n
1
}, and for
any deterministic algorithm for the intersection problem, there is an instance of
signature at most (k, n
1
, . . . , n
k
), and redundancy at most ρ, such that this algorithm
performs Ω(kρ
P
i
log(n
i
/kρ)) comparisons on it.
ACM Journal Name, Vol. V, No. N, October 2006.

Alternation and Redundancy Analysis of the Intersection Problem · 15
ρ
2
≤
2
k
ρ
3
= 1ρ
1
= 1
Fig. 6. Element x is present in
half of the arrays of the sub-
instance.
ρ
1
= 1
Fig. 7. The adversary performs several strategies in parallel, one
for each sub-instance.
Proof. The proof uses the same decomposition than the proof of Theorem 4.10,
but uses an adversary argument to obtain a deterministic lower bound. Build
δ = kρ/3 sub-instances of signature (k, ⌊n
1
/δ⌋, . . . , ⌊n
k
/δ⌋), redundancy at most 3,
such that x = A
1
[1] is present in roughly half of the other arrays, as in Figure 6 .
On each sub-instance an adversary can for c e any deterministic algorithm to
perform a search in each of the arrays co ntaining x, and in a single array which does
not contain x. Then the deterministic algorithm performs (1/2 )
P
k
i=2
log (n
i
/δ)
comparisons for each sub-instance. In total over all sub-instance s, the adversary
can force any deterministic algorithm to per form (δ/2)
P
k
i=2
log (n
i
/δ) comparisons,
i.e. (kρ/4)
P
k
i=2
log (n
i
/kρ), which is Ω(kρ
P
k
i=2
log (n
i
/kρ)).
As x log(n/x) is a function increasing with x, kρ
P
i
log(n
i
/kρ) is several times
larger than the lower bound ρ
P
i
log(n
i
/ρ), hence no deterministic algorithm can
be optimal in the redundancy analysis.
Theorem 5.2. Any algorithm optimal in the redundancy analysis is optimal in
the alternation analysis.
Proof. By definition of the redundancy ρ and of the alternation δ of an ins tance,
ρ ≤ δ. So if an algorithm performs O(ρ
P
log n
i
/ρ) comparisons, it also performs
O(δ
P
log n
i
/δ) comparisons. Hence the result, as this is the lower bound in the
alternation analysis .
This proves also that the measure of difficulty of Demaine et al. [2000] is not
comparable w ith the measure of redundancy, as it is not comparable with the
measure of alternation [Barbay and Kenyon 2003, Section 2.3]. This mea ns that
the two measures are complementary, without being redundant in any way, as it
was for the alternation. All those measures describe the difficulty of the instance:
—the alternation [Barbay and Kenyon 2003, Section 2.3] describes the number of
key blocks of consecutive elements in the instance;
—the gap cost [Demaine et al. 2000] describe s the repartition o f the size of those
blocks;
—the redundancy [Barbay 2003] describe s the difficulty to find each block.
But only the gap cost and the redundancy matter, because the alternation analysis
is reduced to the redundancy analy sis.
ACM Journal Name, Vol. V, No. N, October 2006.

16 · J. Barbay and C. Kenyon
6. PERSPECTIVES
The t-threshold set and opt-threshold set problems [Barbay and Kenyon 2003] a re
natural g e neralizations of the inters e c tion problem, which could be useful in indexed
search engines. The redundancy seems to be important in the complexity of these
problems as well, but a proper measure is harder to define in this context. As similar
techniques are applied to solve queries on s e mi- structured documents [Barbay 2004],
the redundancy could be useful in this domain too, but the definition of the proper
measure of difficulty is even more evasive in this context.
Demaine et al. [2001] performed experimental measurements of the performance
of various deterministic algo rithms for the intersection on their own data using
some queries provided by Google. We perfo rmed similar measurements for the
deterministic and randomized version of our algorithm, using the same queries and
a larger set of data, also provided by Google. The results are quite disappointing,
as the randomized version of the algorithm does not perform better than the
deterministic one in term of the number of comparisons or searches, and much worst
in term of runtime. The fact that the number of comparisons and the number of
searches are roughly the same indicates that most instances of this data set either
have a redundancy close to the alternation, because the elements searched are in
many of the arrays, or are so easy that both algorithms perform equally well on
it. The fact that the runtime is worse is probably linked to the performance of
prediction heuristics in the hardware: a deterministic algorithm is easier to predict
than a randomized one. It would be interesting to see if those negative results still
holds for queries with more keywords and on some data sets such as those from
relational databases, which can exhibit more correlatio n b e tween keywords.
While we restricted our definition of the intersection problem to set of arrays and
analyzed it in the comparis on model, it makes sense to consider other structures
for sorted sets, especially in the context of cached or swapped memory, or succinct
encodings of dictionaries. The hierarchical memory [Frigo et al. 1 999] s e ems promising
for this kind of applica tion, and Bender et al. [2002] proposed a data structure
and a cache oblivious algorithm to perform unbounded searches (implemented as
finger searches). Our algorithm can easily be a dapted to this model, to perform
O(ρ
P
(log
B
(n
i
/ρ) + log
∗
(n
i
/ρ))) I/O transfers at the level of cache size B.
In most of the intersection algorithms, the interactions with each set are limited
to accessing an element given its rank (select o perator) and searching for the
insertion rank of an element in it (rank operator ): those algorithms can be used
with any set implementation which provides those op e rators. For instance , using
sorted arrays such as in this paper, the select operator takes constant time while
the rank operato r takes logarithmic time in the size of the set. While the results of
this paper are optimal in the comparison model, it is not necess ary optimal in more
general models: the computational complexity of the search operators is a trade-off
with the size of the encoding o f the set. For instance, consider a set of n elements
from a universe of size m: Rama n et al. [2002] propose a succinct encoding of
Fully Indexable Dictionaries using log
m
n
+ o(m) bits to provide select and rank
operators in constant time. On the other side of the time/space trade-off, Beame
and Fich [2002] proposed a more compact encoding, using O(n) wo rds of log m
bits to provide select and rank opera tors in time O(
p
log n / log log n). Encoding
ACM Journal Name, Vol. V, No. N, October 2006.
Alternation and Redundancy Analysis of the Intersection Problem · 17
the sets using any of those schema would tremendously improve the computational
complexity of the intersection, at a small cost in space, which could result in much
faster search engines.
ACKNOWLEDGMENTS
This paper covers work performed in many places including the University of Paris-
Sud, Orsay, France; the University of British Columbia, Vancouver, Canada; and
the University of Waterloo, Waterloo, Canada. The authors wish to thank all the
institutions involved, as well as Joe l Friedman and the reviewers who provided
many useful comments.
REFERENCES
Baeza-Yates, R. A. 2004. A fast set i ntersection algorithm for sorted sequences. In CPM, S. C.
Sahinalp, S. Muthukrishnan, and U. Dogrus¨oz, Eds. Lecture Notes in Computer Science, vol.
3109. Spr inger, 400–408.
Barbay, J. 2003. Optimality of randomized algorithms for the intersection problem. In
Proceedings of the Symposium on Stochastic Algorithms, Foundations and Applications (SAGA
2003), in Lecture Notes in Computer Science, A. Albrecht, Ed. Vol. 2827 / 2003. Springer-
Verlag Heidelberg, 26–38. 3-540-20103-3.
Barbay, J. 2004. Index-trees for descendant tree queries in the comparison model. Tech. Rep.
TR-2004-11, University of Br itish Columbia. July.
Barbay, J. and Kenyon, C. 2002. Adaptive intersection and t- threshold problems. In Proceedings
of the thirteenth ACM-SIAM Symposium On Discrete Algorithms (SODA). ACM-SIAM, ACM,
390–399.
Barbay, J . and Kenyon, C. 2003. Deterministic algorithm for the t-threshold set problem.
In Lecture Notes in Computer Science, H. O. Toshi hide Ibaraki, Noki Katoh, Ed. Springer-
Verlag, 575–584. Proceedings of the 14th Annual International Symposium on Algorithms And
Computation (ISAAC).
Beame, P. and Fich, F. E. 2002. Optimal bounds for the predecessor problem and related
problems. J. Comput. Syst. Sci. 65, 1, 38–72.
Bender, M. A., Cole, R., a nd Raman, R. 2002. Exponential structures for efficient cache-
oblivious al gorithms. In Proceedings of the 29th International Colloquium on Automata,
Languages and Programming. Springer-Verlag, 195–207.
Bentley, J. L. and Yao, A. C.-C. 1976. An almost optimal algorithm for unbounded searching.
Information processing letters 5, 3, 82–87.
Chaudhuri, S. 1998. An overview of query optimization in relational systems. 34–43.
Christen, C. 1978. Improving the bound on optimal merging. In Proceedings of 19th FOCS.
259–266.
de la Vega, W. F., Frieze, A. M., and Santha, M. 1998. Average-case analysis of the merging
algorithm of hwang and lin. Algorithmica 22, 4, 483–489.
de la Vega, W. F., Kannan, S., and Santha, M. 1993. Two probabilistic results on merging.
SIAM J. Comput. 22, 2, 261–271.
Demaine, E. D., L
´
opez-Ortiz, A., and Munro, J. I. 2000. Adaptive set intersections, unions,
and differences. In Proceedings of the 11
th
ACM-SIAM Symposium on Discrete Algorithms
(SODA). 743–752.
Demaine, E. D., L
´
opez-Ortiz, A., and Munro, J. I. 2001. Experiments on adaptive set
intersections for text retrieval systems. In Proceedings of the 3rd Workshop on Algorithm
Engineering and Experiments, Lecture Notes in Computer Science. Washington DC, 5–6.
Frigo, M., Leiserson, C. E., Prokop, H., and Ramachandran, S. 1999. Cache-oblivious
algorithms. In Proceedings of the 40th Annual Symposium on Foundations of Computer
Science. IEEE Computer Society, 285.
ACM Journal Name, Vol. V, No. N, October 2006.
18 · J. Barbay and C. Kenyon
Hwang, F. K. an d Lin, S. 1971. Optimal merging of 2 elements wi th n elements. Acta
Informatica, 145–158.
Hwang, F. K. and Lin, S. 1972. A simple algorithm for merging two disjoint linearly ordered
sets. SIAM Journal of Computing 1, 1, 31–39.
Manacher, G . K. 1979. Significant improvements to the hwang-ling mer ging algorithm.
JACM 26, 3, 434–440.
Neumann, J. V. and M orgenstern, O. 1944. Theory of games and economic behavior. 1st ed.
Princeton University Press.
Raman, R., Raman, V., and Rao, S. S. 2002. Succinct i ndexable dictionaries with applications to
encoding k-ary trees and multisets. In SODA ’02: Proceedings of the thirteenth annual ACM-
SIAM symposium on Discrete algorithms. Society for Industrial and Applied Mathematics,
Philadelphia, PA, USA, 233–242.
Sion, M. 1958. On general minimax theorems. Pacic Journal of Mathematics, 171–176.
Witten, I. H., Moffat, A., a nd Bell, T. C. 1994. Managing Gigabytes. VanNostrand Reinhold,
115 Fifth Avenue, New York, NY 10003.
Yao, A. C. 1977. Probabilistic computations: Toward a unified measure of complexity. In Proc.
18th IEEE Symposium on Foundations of Computer Science (FOCS). 222–227.
ACM Journal Name, Vol. V, No. N, October 2006.
