Outline
1
Quadratic Equations and Functions
Solve Quadratic Equations Using the Square Root Property
Solve Quadratic Equations by Completing the Square
Solve Quadratic Equations Using the Quadratic Formula
Solve Quadratic Equations in Quadratic Form
Solve Applications of Quadratic Equations
Graph Quadratic Functions Using Properties
Graph Quadratic Functions Using Transformations
Solve Quadratic Inequalities
George Voutsadakis (LSSU) Intermediate Algebra August 2020 2 / 113

Quadratic Equations and Functions Solve Quadratic Equations Using the Square Root Property
We Shall Learn and Practice
Solve quadratic equations of the form ax
2
= k using the Square Root
Property.
Solve quadratic equations of the form a(x −h)
2
= k using the Square
Root Property.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 4 / 113

Quadratic Equations and Functions Solve Quadratic Equations Using the Square Root Property
Quadratic Equations of the Form ax
2
= k
The Square Root Property: If x
2
= k, then
x =
√
k or x = −
√
k.
This i s sometimes abbreviated by writing x = ±
√
k.
To solve an equation of the form ax
2
= k follow the steps:
Isolate the quadratic term and make its coefficient 1;
Use the Square R oo t Property;
Simplify the radical;
Check the solutions.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 5 / 113

Quadratic Equations and Functions Solve Quadratic Equations Using the Square Root Property
Quadratic Equations of the Form a(x − h)
2
= k
To solve a quadratic equation of the form a(x − h)
2
= k, follow the
steps:
Isolate the term that has the variable squared;
In this case, a binomial is being squ ared.
Once the binomial is isol ated, by di viding each side by the coefficient a,
we make the coefficient of (x − h)
2
equal to 1;
Then we use the Square Root Property on (x − h)
2
.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 11 / 113

Quadratic Equations and Functions Solve Quadratic Equations Using the Square Root Property
Example
Solve: 5(a − 5)
2
+ 4 = 104.
5(a − 5)
2
+ 4 = 104
5(a − 5)
2
= 100
(a − 5)
2
= 20
a − 5 = ±
√
20
a − 5 = ±
√
4
√
5
a − 5 = ±2
√
5
a = 5 ± 2
√
5.
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 14 / 113

Quadratic Equations and Functions Solve Quadratic Equations Using the Square Root Property
Example
Solve: (3r + 4)
2
= −8.
(3r + 4)
2
= −8
3r + 4 = ±
√
−8
3r + 4 = ±
√
8i
3r + 4 = ±
√
4
√
2i
3r + 4 = ±2
√
2i
3r = −4 ± 2
√
2i
r = −
4
3
±
2
√
2
3
i.
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 15 / 113

Quadratic Equations and Functions Solve Quadratic Equations by Completing the Square
We Shall Learn and Practice
Complete the square of a binomial expression.
Solve quadratic equations of the form x
2
+ bx + c = 0 by completing
the sq u are.
Solve quadratic equations of the form ax
2
+ bx + c = 0 by
completing the square.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 18 / 113

Quadratic Equations and Functions Solve Quadratic Equations by Completing the Square
Complete the Square of a Binomial Expression
This technique is b ased on
(a + b)
2
= a
2
+ 2 · a · b + b
2
;
(a − b)
2
= a
2
− 2 · a · b + b
2
.
To complete a square of x
2
+ bx follow the steps:
Identify b, the coefficient o f x;
Find (
1
2
b)
2
, the number to complete the square;
Add the (
1
2
b)
2
to x
2
+ bx;
Factor the perfect square trinomial, writing it as a b inomial squared.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 19 / 113

Quadratic Equations and Functions Solve Quadratic Equations by Completing the Square
Example
Complete the square to make a perfect square trin omia l. Then write
the resul t a s a bi n omia l s q u ared. (a) a
2
− 20a (b) m
2
− 5m (c)
p
2
+
1
4
p
(a)
a
2
− 20a (
1
2
b)
2
= (
1
2
20)
2
= 10
2
= 100;
a
2
− 20a + 100 = a
2
− 2 · a · 10 + (10)
2
= (a − 10)
2
;
(b)
m
2
−5m (
1
2
b)
2
= (
1
2
5)
2
= (
5
2
)
2
=
25
4
;
m
2
− 5m +
25
4
= m
2
− 2 · m ·
5
2
+ (
5
2
)
2
= (m −
5
2
)
2
;
(c)
p
2
+
1
4
p (
1
2
b)
2
= (
1
2
1
4
)
2
= (
1
8
)
2
=
1
64
;
p
2
+
1
4
p +
1
64
= p
2
+ 2 · p ·
1
8
+ (
1
8
)
2
= (p +
1
8
)
2
.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 20 / 113

Quadratic Equations and Functions Solve Quadratic Equations by Completing the Square
Quadratic Equations of the Form x
2
+ bx + c = 0
To solve quadratic equations of the form x
2
+ bx + c = 0 by
completing the square follow the steps:
Isolate the variable terms on one side and the constan t terms on the
other;
Find (
1
2
b)
2
, the number to complete the square, and add it to both
sides;
Factor the perfect square trinomial as a binomial square;
Use the Square Root Property;
Simplify the radical and then solve the two resu lting equations;
Check the solutions.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 21 / 113

Quadratic Equations and Functions Solve Quadratic Equations by Completing the Square
Example
Solve by completing the square: y
2
− 10y = − 35.
y
2
− 10y = − 35
y
2
− 10y + 25 = −35 + 25
(y − 5)
2
= − 10
y − 5 = ±
√
−10
y − 5 = ±
√
10i
y = 5 ±
√
10i.
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 23 / 113

Quadratic Equations and Functions Solve Quadratic Equations by Completing the Square
Example
Solve by completing the square: x
2
− 16x = −16.
x
2
− 16x = −16
x
2
− 16x + 64 = −16 + 64
(x − 8)
2
= 48
x − 8 = ±
√
48
x − 8 = ±
√
16
√
3
x − 8 = ±4
√
3
x = 8 ± 4
√
3.
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 24 / 113

Quadratic Equations and Functions Solve Quadratic Equations by Completing the Square
Example
Solve by completing the square: a
2
+ 4a + 9 = 30.
a
2
+ 4a + 9 = 30
a
2
+ 4a = 21
a
2
+ 4a + 4 = 21 + 4
(a + 2)
2
= 25
a + 2 = ±
√
25
a + 2 = ±5
a = −2 ± 5
a = −7 or a = 3.
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 25 / 113

Quadratic Equations and Functions Solve Quadratic Equations by Completing the Square
Example
Solve by completing the square: p
2
= 5p + 9.
p
2
= 5p + 9
p
2
− 5p = 9
p
2
− 5p +
25
4
= 9 +
25
4
(p −
5
2
)
2
=
61
4
p −
5
2
= ±
q
61
4
p −
5
2
= ±
√
61
2
p =
5
2
±
√
61
2
p =
5±
√
61
2
.
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 26 / 113

Quadratic Equations and Functions Solve Quadratic Equations by Completing the Square
Example
Solve by completing the square: (c − 2)(c + 8) = 11.
(c − 2)(c + 8) = 11
c
2
+ 6c − 16 = 11
c
2
+ 6c = 27
c
2
+ 6c + 9 = 27 + 9
(c + 3)
2
= 36
c + 3 = ±
√
36
c + 3 = ±6
c = −3 ± 6
c = −9 or c = 3.
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 27 / 113

Quadratic Equations and Functions Solve Quadratic Equations by Completing the Square
Quadratic Equations of the Form ax
2
+ bx + c = 0
The process of completing the s q u are works best when th e coefficient
of x
2
is 1.
If the x
2
term has a coefficient other t h an 1, we take some
preliminary st eps to make t h e coefficient equal to 1.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 28 / 113

Quadratic Equations and Functions Solve Quadratic Equations by Completing the Square
Example
Solve by completing the square: 2m
2
+ 16m + 14 = 0.
2m
2
+ 16m + 14 = 0
m
2
+ 8m + 7 = 0
m
2
+ 8m = −7
m
2
+ 8m + 16 = −7 + 16
(m + 4)
2
= 9
m + 4 = ±
√
9
m + 4 = ±3
m = −4 ± 3
m = −7 or m = −1.
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 29 / 113

Quadratic Equations and Functions Solve Quadratic Equations by Completing the Square
Example
Solve by completing the square: 3r
2
− 2r = 21.
3r
2
− 2r = 21
r
2
−
2
3
r = 7
r
2
−
2
3
r +
1
9
= 7 +
1
9
(r −
1
3
)
2
=
64
9
r −
1
3
= ±
q
64
9
r −
1
3
= ±
8
3
r =
1
3
±
8
3
r = −
7
3
or r = 3.
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 30 / 113

Quadratic Equations and Functions Solve Quadratic Equations Using the Quadratic Formula
We Shall Learn and Practice
Solve quadratic equations using the Quadratic Formula.
Use the Discriminant to predi ct the number and type of solutions of a
quadratic equation.
Identify the most appropriate method to use to solve a quadra tic
equation.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 32 / 113

Quadratic Equations and Functions Solve Quadratic Equations Using the Quadratic Formula
Solve Quadratic Equations Using the Quadratic Formula
Quadratic Formula: The solutions to a quadratic equation of the
form
ax
2
+ bx + c = 0, where a 6= 0,
are given by the formula:
x =
−b ±
√
b
2
− 4ac
2a
.
To u se the Quadratic Formula follow the steps:
Write the quadratic equation in standard form to identi fy the values of
a, b and c;
Write the quadratic formula and substitu te in the values of a, b and c;
Simply the fraction and solve for x;
Check the solution(s).
George Voutsadakis (LSSU) Intermediate Algebra August 2020 33 / 113

Quadratic Equations and Functions Solve Quadratic Equations Using the Quadratic Formula
Example
Solve by using the Quadratic Formula: 3y
2
− 5y + 2 = 0.
We h ave a = 3, b = − 5 and c = 2.
We set up the quadratic formula:
x =
−b ±
√
b
2
− 4ac
2a
=
−(−5) ±
p
(−5)
2
− 4 · 3 · 2
2 · 3
=
5 ±
√
1
6
=
5 ± 1
6
=
2
3
1
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 34 / 113

Quadratic Equations and Functions Solve Quadratic Equations Using the Quadratic Formula
Example
Solve by using the Quadratic Formula: a
2
− 2a = 15.
Rewrite in standard form a
2
−2a − 15 = 0.
We h ave a = 1, b = − 2 and c = − 15.
We set up the quadratic formula:
x =
−b ±
√
b
2
− 4ac
2a
=
−(−2) ±
p
(−2)
2
− 4 · 1 · (−15)
2 · 1
=
2 ±
√
64
2
=
2 ± 8
2
=
−3
5
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 35 / 113

Quadratic Equations and Functions Solve Quadratic Equations Using the Quadratic Formula
Example
Solve by using the Quadratic Formula: 3m
2
+ 12m + 7 = 0.
We h ave a = 3, b = 12 and c = 7.
We set up the quadratic formula:
x =
−b ±
√
b
2
− 4ac
2a
=
−12 ±
√
12
2
− 4 · 3 · 7
2 · 3
=
−12 ±
√
60
6
=
−12 ±
√
4
√
15
6
=
−12 ± 2
√
15
6
=
2(−6 ±
√
15)
6
=
−6 ±
√
15
3
.
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 36 / 113

Quadratic Equations and Functions Solve Quadratic Equations Using the Quadratic Formula
Example
Solve by using the Quadratic Formula: 4a
2
− 2a + 8 = 0.
We may simplify first: 2a
2
− a + 4 = 0.
We h ave a = 2, b = − 1 and c = 4.
We set up the quadratic formula:
x =
−b ±
√
b
2
− 4ac
2a
=
−(−1) ±
p
(−1)
2
− 4 · 2 · 4
2 · 2
=
1 ±
√
−31
4
=
1 ±
√
31i
4
.
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 37 / 113

Quadratic Equations and Functions Solve Quadratic Equations Using the Quadratic Formula
Example
Solve by using the Quadratic Formula: x(x + 2) − 5 = 0.
Rewrite in standard form: x
2
+ 2x − 5 = 0.
We h ave a = 1, b = 2 and c = − 5.
We set up the quadratic formula:
x =
−b ±
√
b
2
−4ac
2a
=
−2 ±
p
2
2
− 4 · 1 · (−5)
2 · 1
=
−2 ±
√
24
2
=
−2 ±
√
4
√
6
2
=
−2 ± 2
√
6
2
=
2(−1 ±
√
6)
2
= − 1 ±
√
6.
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 38 / 113

Quadratic Equations and Functions Solve Quadratic Equations Using the Quadratic Formula
Example
Solve by using the Quadratic Formula:
1
4
c
2
−
1
3
c =
1
12
.
Rewrite in standard form:
1
4
c
2
−
1
3
c −
1
12
= 0.
Multiply by the LCD to clear denominators:
12(
1
4
c
2
−
1
3
c −
1
12
) = 12 · 0
3c
2
− 4c − 1 = 0.
We h ave a = 3, b = − 4 and c = − 1.
We set up the quadratic formula:
x =
−b ±
√
b
2
− 4ac
2a
=
−(−4) ±
p
(−4)
2
− 4 · 3 · (−1)
2 · 3
=
4 ±
√
28
6
=
4 ±
√
4
√
7
6
=
4 ± 2
√
7
6
=
2 ±
√
7
3
.
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 39 / 113

Quadratic Equations and Functions Solve Quadratic Equations Using the Quadratic Formula
Discriminant to Predict the Number and Type of Solutions
In th e quadratic formula
x =
−b ±
√
b
2
− 4ac
2a
the quantity
D = b
2
− 4ac
is called the discriminant.
To u se the discrimi n ant, b
2
− 4ac, to determine the n u mber and type
of solut ions of a quad ratic equation, follow the steps:
If b
2
− 4ac > 0, the equation has 2 real solutions;
If b
2
− 4ac = 0, the equation has 1 real solution;
If b
2
− 4ac < 0, the equation has 2 complex solutions.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 40 / 113

Quadratic Equations and Functions Solve Quadratic Equations Using the Quadratic Formula
Example
Determine the number and type of solutions to each quadrat ic
equation. (a) 8m
2
− 3m + 6 = 0 (b) 5z
2
+ 6z − 2 = 0 (c)
9w
2
+ 24w + 16 = 0.
(a) Compute
b
2
− 4ac = (−3)
2
− 4 · 8 · 6 = 9 − 192 = − 183 < 0.
Thus, 8m
2
− 3m + 6 = 0 has two complex solutions;
(b) Compute
b
2
− 4ac = 6
2
− 4 · 5 · (−2) = 36 + 40 = 76 > 0.
Thus, 5z
2
+ 6z − 2 = 0 has two real solutions;
(c) Compute
b
2
− 4ac = 24
2
− 4 · 9 · 16 = 576 − 576 = 0.
Thus, 9w
2
+ 24w + 16 = 0 has one real solution.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 41 / 113

Quadratic Equations and Functions Solve Quadratic Equations Using the Quadratic Formula
Identify the Most Appropriate Solution Method
To identify the most appropriate method to solve a quadratic
equation:
We try Factoring first.
If the quadratic factors easily, this method is very quick;
Try the Square Root Property next.
If the equation fits the form ax
2
= k or a(x − h)
2
= k, it can easily be
solved by using the Square Root Property;
Use the Quadratic Formula.
Any ot her quadratic e quation is best solved by using the Quadratic
Formula.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 42 / 113

Quadratic Equations and Functions Solve Quadratic Equations Using the Quadratic Formula
Example
Identify the most appropriate method to use to solve each quad ratic
equation. (a) x
2
+ 6x + 8 = 0 (b) (n − 3)
2
= 16 (c) 5p
2
− 6p = 9.
(a) Since f actoring x
2
+ 6x + 8 is easy, the factoring method works best.
(b) Since the equation has form (x − h)
2
= k, the Square Root Property
works best.
(c) Rewrite 5p
2
− 6p − 9 = 0.
It s eems like factoring is either difficult or impossible. So the
quadratic formula may be the best method.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 43 / 113

Quadratic Equations and Functions Solve Quadratic Equations in Quadratic Form
Solve Equations in Quadratic Form
To solve equations in quadratic form follow the steps:
Identify a substitution that will put the equation in quadratic form;
Rewrite the equation with the substitution to put it in quadratic form;
Solve the quadratic equa t ion for u;
Substitute t he original variable b a ck into the results, using the
substitution ;
Solve for the original variable;
Check the solutions.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 46 / 113

Quadratic Equations and Functions Solve Quadratic Equations in Quadratic Form
Example
Solve: x
4
− 6x
2
+ 8 = 0.
Set u = x
2
. Then u
2
= (x
2
)
2
= x
4
.
Substitute: u
2
− 6u + 8 = 0.
Solve for u:
u
2
− 6u + 8 − 0
(u − 4)(u − 2) = 0
u = 4 or u = 2.
Go back to the substitution formula to get equations for x:
x
2
= 2 or x
2
= 4
x = ±
√
2 or x = ±
√
4
x = ±
√
2 or x = ±2.
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 47 / 113

Quadratic Equations and Functions Solve Quadratic Equations in Quadratic Form
Example
Solve: (x − 5)
2
+ 6(x − 5) + 8 = 0.
Set u = x − 5. Then u
2
= (x − 5)
2
.
Substitute: u
2
+ 6u + 8 = 0.
Solve for u:
u
2
+ 6u + 8 − 0
(u + 2)(u + 4) = 0
u = −2 or u = −4.
Go back to the substitution formula to get equations for x:
x − 5 = −2 or x − 5 = −4
x = 3 or x = 1.
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 48 / 113

Quadratic Equations and Functions Solve Quadratic Equations in Quadratic Form
Example
Solve: x − 7
√
x + 12 = 0.
Set u =
√
x. Then u
2
= (
√
x)
2
= x.
Substitute: u
2
− 7u + 12 = 0.
Solve for u:
u
2
− 7u + 12 = 0
(u − 3)(u − 4) = 0
u = 3 or u = 4.
Go back to the substitution formula to get equations for x:
√
x = 3 or
√
x = 4
x = 3
2
or x = 4
2
x = 9 or x = 16.
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 49 / 113

Quadratic Equations and Functions Solve Quadratic Equations in Quadratic Form
Example
Solve: x
2
3
− 5x
1
3
− 14 = 0.
Set u = x
1
3
. Then u
2
= (x
1
3
)
2
= x
2
3
.
Substitute: u
2
− 5u − 14 = 0.
Solve for u:
u
2
− 5u − 14 = 0
(u − 7)(u + 2) = 0
u = 7 or u = −2.
Go back to the substitution formula to get equations for x:
x
1
3
= 7 or x
1
3
= −2
3
√
x = 7 or
3
√
x = −2
x = 7
3
or x = (−2)
3
x = 343 or x = −8.
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 50 / 113

Quadratic Equations and Functions Solve Quadratic Equations in Quadratic Form
Example
Solve: 8x
−2
− 10x
−1
+ 3 = 0.
Set u = x
−1
. Then u
2
= (x
−1
)
2
= x
−2
.
Substitute: 8u
2
− 10u + 3 = 0.
Solve for u:
8u
2
− 10u + 3 = 0
8u
2
− 4u − 6u + 3 = 0
4u(2u − 1) − 3(2u − 1) = 0
(4u − 3)(2u − 1) = 0
u =
3
4
or u =
1
2
.
Go back to the substitution formula to get equations for x:
x
−1
=
3
4
or x
−1
=
1
2
x =
4
3
or x = 2.
Check th e solutions!
George Voutsadakis (LSSU) Intermediate Algebra August 2020 51 / 113

Quadratic Equations and Functions Solve Applications of Quadratic Equations
Solve Applications Modeled by Quadratic Equations
Follow t h e steps:
Read th e problem carefully;
Identify what we are look ing for and choo se a variable to represent that
quantity;
Translate into an equa t ion;
Solve the equatio n using algebra techniques;
Check the answer in the problem and make sure it makes sense;
Answer the question with a complete sentence.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 54 / 113

Quadratic Equations and Functions Solve Applications of Quadratic Equations
Example
The product of two consecutive o d d in tegers is 99. Find the integers.
Suppose n and n + 2 are the two consecutive odd i n tegers.
Since their product is 99, we get n(n + 2) = 99.
We solve for n to find the i n tegers.
n(n + 2) = 99
n
2
+ 2n = 99
n
2
+ 2n − 99 = 0
(n − 9)(n + 11) = 0
n = 9 or n = −11.
Hence the two integers are either 9 a n d 11 or −11 and −9.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 55 / 113

Quadratic Equations and Functions Solve Applications of Quadratic Equations
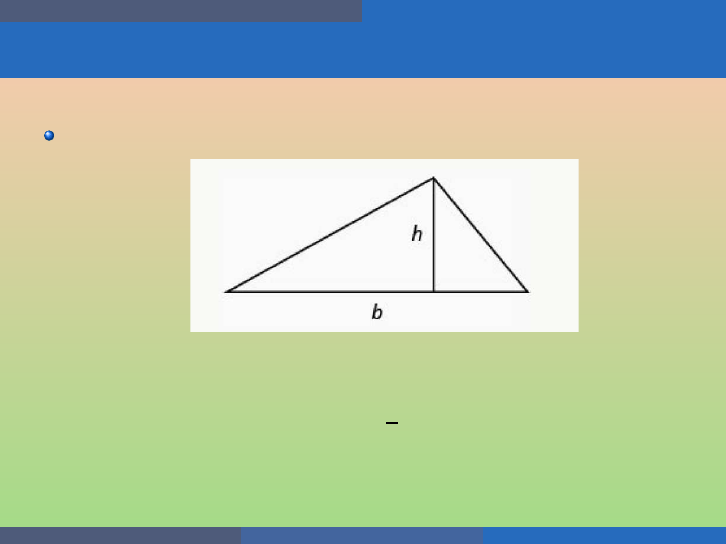
Example
Find the base and height of a trian gle whose b ase is four inches more
than six times its height and has an area of 456 square inches.
Let b be the base and h be the height of th e given triangle.
The base is four in ches more than six times the height. So we have
the equation b = 6h + 4.
Moreover, we know tha t the area is given by A =
1
2
bh.
So we get the equation:
1
2
(6h + 4)h = 456
(3h + 2)h = 456
3h
2
+ 2h − 456 = 0
h =
−2 ±
p
2
2
− 4 · 3 · (−456)
2 · 3
=
−2 ±
√
5476
6
=
−2 ± 74
6
=
72
6
= 12.
Hence, the triangle has height 12 in ches and b ase b = 76 inches.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 57 / 113

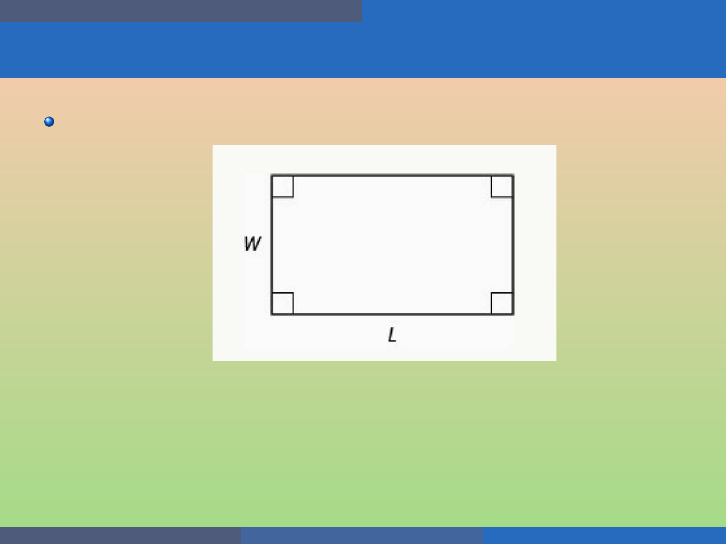
Quadratic Equations and Functions Solve Applications of Quadratic Equations
Example
The length of a 200 square foot rectangular vegetable garden is four
feet less than twice the wid th. Find th e length and width of the
gard en, to the nearest tenth of a foot.
Let L be the width and W be the length of the garden.
The length i s four feet less than twice the wid th: L = 2W − 4.
Moreover, t h e area is given by A = LW .
So we get the equation:
(2W −4)W = 200
2W
2
− 4W = 200
2W
2
− 4W − 200 = 0
W
2
− 2W − 100 = 0
W =
−(−2) ±
p
(−2)
2
− 4 · 1 · (−100)
2 · 1
=
2 ±
√
404
2
≈ 11.
Hence, the garden has width ≈ 11 inches and length L ≈ 18 inches.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 59 / 113
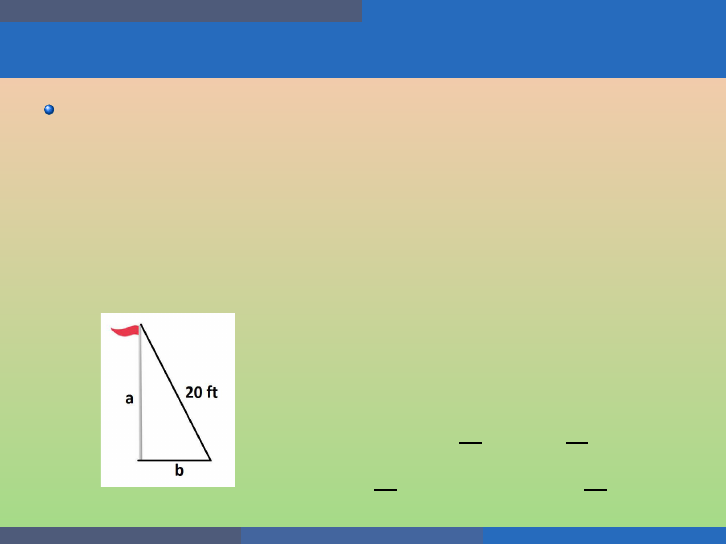
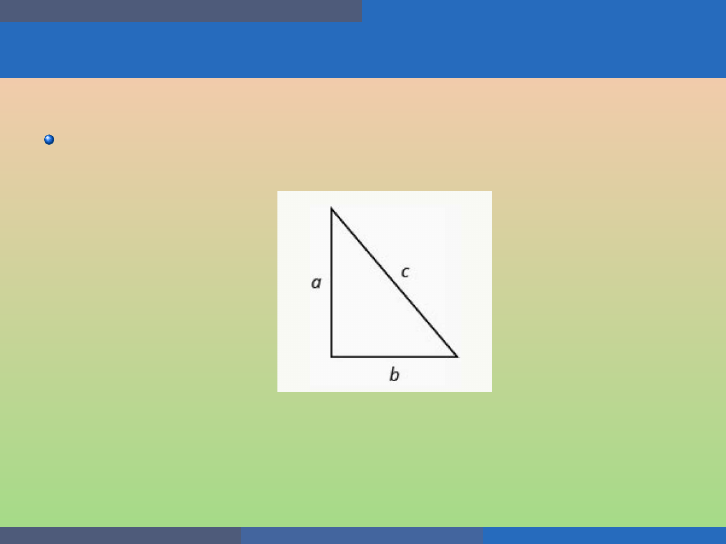
Quadratic Equations and Functions Solve Applications of Quadratic Equations
Example
The su n casts a shadow from a flag pole. The height of the flag pole
is three ti mes the length of its shadow. The distance between the end
of the shadow and the top of the flag pole is 20 feet. Find the length
of the shadow and the length of the flag pole.
Let a be the length of the flag pole and b the length of th e shadow.
The height of the pole is three times the length of its shadow: a = 3b.
Moreover, t h e hypothenuse of th e right triangle is 20 ft.
So, by t h e Pythagorean T h eorem, we get the equation:
(3b)
2
+ b
2
= 20
2
9b
2
+ b
2
= 400
10b
2
= 400
b
2
= 40
b = ±
√
40 = ± 2
√
10.
Hence, the sh adow ha s l ength 2
√
10 ft. and the pole 6
√
10 ft.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 61 / 113

Quadratic Equations and Functions Solve Applications of Quadratic Equations
Height of an Object Shot Upward
The height in feet, h, of an object shot upwards into the air with
initial v elocity, v
0
, after t seconds is given by the formula
h = −16t
2
+ v
0
t.
We can use this formula to find how many seconds it will take for the
object to reach a specific height.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 62 / 113

Quadratic Equations and Functions Solve Applications of Quadratic Equations
Example
An arrow is shot from the ground into the air at an initial speed of
108 ft/s. Use the f ormula h = −16t
2
+ v
0
t to determine when the
arrow will be 180 feet from the ground.
Let t be t h e time when t h e arrow wil l be 180 feet from the ground.
Then, sub stituting in h = −16t
2
+ v
0
t, we get:
180 = −16t
2
+ 108t
16t
2
− 108t + 180 = 0
4t
2
− 27t + 45 = 0
4t
2
− 12t − 15t + 45 = 0
4t(t − 3) − 15(t − 3) = 0
(4t − 15)(t − 3) = 0
t =
15
4
or t = 3.
Hence, the object will be at height 180 feet at time t = 3 secs and at
time t = 3.75 secs
George Voutsadakis (LSSU) Intermediate Algebra August 2020 63 / 113

Quadratic Equations and Functions Solve Applications of Quadratic Equations
Uniform Motion
We already encountered the formula
Distance = Velocity × Time
D = rt.
The f ormula D = rt assumes we know r and t an d use them to find
D.
If we know D and r and need to find t, we would solve the equation
for t and get the formula t =
D
r
.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 64 / 113

Quadratic Equations and Functions Solve Applications of Quadratic Equations
Example
MaryAnne just returned from a visit with her grandchildren back east.
The trip was 2400 mil es from her home and her total time in the
airplane for the round trip wa s 10 hours. If the plane was flying at a
rate of 500 miles per hour, what was the speed of the jet stream?
Suppose that the speed of the jet stream is s.
Then the speed of the forward trip was (500 + s) mph an d that of the
return t rip (500 − s) mph.
Assume the forward trip took t hours and the return trip took t
′
hours.
Using t =
D
r
, we get the two equations t =
2400
500+s
and t
′
=
2400
500−s
.
We also know that t + t
′
= 10.
Hence we get th e eqution
2400
500 + s
+
2400
500 − s
= 10.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 65 / 113

Quadratic Equations and Functions Solve Applications of Quadratic Equations
Example (Cont’d)
We solve the equation.
2400
500 + s
+
2400
500 − s
= 10
(500 + s)(500 − s)
2400
500 + s
+
2400
500 − s
= 10(500 + s)(500 − s)
2400(500 − s) + 2400(500 + s) = 10(500 + s)(500 − s)
240(500 − s) + 240(500 + s) = (500 + s)(500 − s)
120000 − 240s + 120000 + 240s = 250000 − s
2
240000 = 250000 − s
2
s
2
= 10000
s = 100.
Thus the s peed of the jet stream was 100 mph.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 66 / 113

Quadratic Equations and Functions Solve Applications of Quadratic Equations
Work
Recall the framework in which
a worker A needs a hours to complete a jo b;
a worker B needs b hours to c omplete the same job.
To find the time t it would take them working together to complete
the same job, we set up the equation
1
t
=
1
a
+
1
b
.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 67 / 113

Quadratic Equations and Functions Solve Applications of Quadratic Equations
Example
Press #1 takes 6 hours more than Press #2 to print a magazine
When both are ru n n ing they can print the magazine in 4 hours. How
long does it take for each press to print the job alone?
Suppose it takes Press #1 t hours to print the job alone.
Then it takes Press #2 t − 6 hours to print the job alone.
Since it takes them together 4 hours to do the job, we get
1
t
+
1
t−6
=
1
4
4t(t − 6)
1
t
+
1
t−6
= 4t(t − 6)
1
4
4(t − 6) + 4t = t(t − 6)
4t − 24 + 4t = t
2
− 6t
t
2
− 14t + 24 = 0
(t − 12)(t − 2) = 0
t = 2 or t = 12.
Hence, it takes Press # 1 12 hours and Press #2 6 hours to do the
job alone.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 68 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Properties
We Shall Learn and Practice
Recognize the graph of a quadratic function.
Find the axis of s y mmetry and v ertex of a parabola.
Find the intercepts of a parabola.
Graph quadratic functions usi n g properties.
Solve maximum and minimum applications.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 70 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Properties
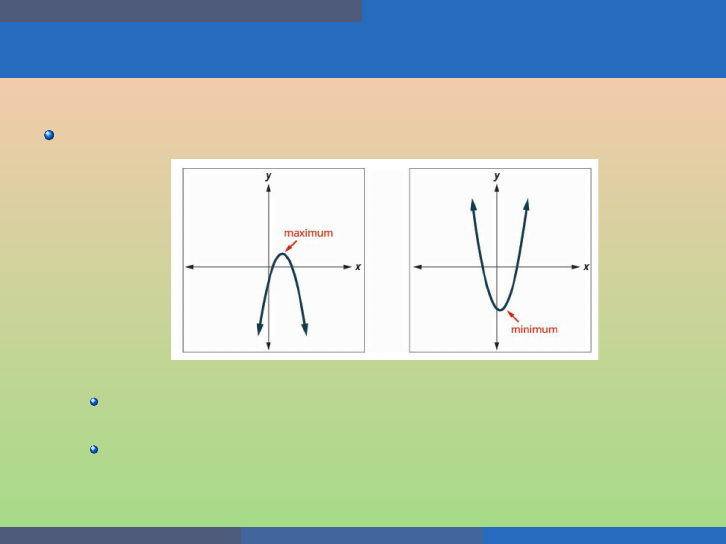
Recognize the Graph of a Quadratic Function
A quadratic function is a function of the form
f (x) = ax
2
+ bx + c,
where a, b, and c are real numbers and a 6= 0.
Every quadratic function has a graph that looks like
We call this figure a parabola.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 71 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Properties
Example
Determine whether the graph of each function is a parabola that
opens upward or downward: (a ) f (x) = 2x
2
+ 5x − 2 (b)
f (x) = −3x
2
− 4x + 7.
(a) In thi s case a = 2 > 0.
So the parabola opens up.
(b) In this case a = − 3 < 0.
So the parabola opens down.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 74 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Properties
Axis of Symmetry and Vertex of a Parabola
The graph of the function
f (x) = ax
2
+ bx + c
is a parabola where:
The axis of symmetry is the vertical li ne x = −
b
2a
;
The vertex is a point on the axis of symmetry, so its x-coordinate is
−
b
2a
;
The y -coordinate of the vertex is found by subs t ituting x = −
b
2a
into
the quadratic equation, i.e., we compute f (−
b
2a
).
George Voutsadakis (LSSU) Intermediate Algebra August 2020 75 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Properties
Example
For the graph of f (x) = 2x
2
− 8x + 1 find: (a) the axis of symmetry
(b) the vertex.
(a) The axis of symmetry is the vertical line
x = −
b
2a
= −
−8
2 · 2
=
8
4
= 2.
(b) The x-co ordinate of the vertex is x = 2.
To find the y -coordinate, we calcula te
f (2) = 2 · 2
2
− 8 · 2 + 1 = 8 − 16 + 1 = − 7.
Thus the vertex is the point (2, −7).
George Voutsadakis (LSSU) Intermediate Algebra August 2020 76 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Properties
Intercepts of a Parabola
To find the intercepts of a parabola whose function is
f (x) = ax
2
+ bx + c
follow the steps:
For the y-intercept set x = 0 and sol ve for y;
For the x-i n t ercepts set y = 0 an d solve for x.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 77 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Properties
Example
Find the intercepts of t h e parabola whose function is
f (x) = x
2
+ 2x − 8.
For the y-intercept, set x = 0 and compute:
f (0) = 0
2
+ 2 · 0 − 8 = − 8.
Thus the y -intercept is (0, −8).
For the x-intercepts, set y = 0 and compute:
x
2
+ 2x − 8 = 0
(x − 2)(x + 4) = 0
x = 2 or x = −4.
Thus, the x-intercepts are (−4, 0) and (2, 0).
George Voutsadakis (LSSU) Intermediate Algebra August 2020 78 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Properties
Example
Find the intercepts of t h e parabola whose function is
f (x) = 3x
2
+ 4x + 4.
For the y-intercept, set x = 0 and compute:
f (0) = 3 · 0
2
+ 4 · 0 + 4 = 4.
Thus the y -intercept is (0, 4).
For the x-intercepts, set y = 0:
3x
2
+ 4x + 4 = 0.
We h ave
D = b
2
− 4ac = 4
2
−4 · 3 · 4 = 16 − 48 = − 32 < 0.
Hence, 3x
2
+ 4x + 4 = 0 does not have any real roots.
It follows th at f (x) has no x-intercepts.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 79 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Properties
Graph Quadratic Functions Using Properties
To graph a qua d ratic function follow the steps:
Determine wh ether the parabola opens up or down;
Find the vertex and the axis of symmetry;
Find the y - and the x-intercepts;
Find additional points if needed;
Plot the graph.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 80 / 113
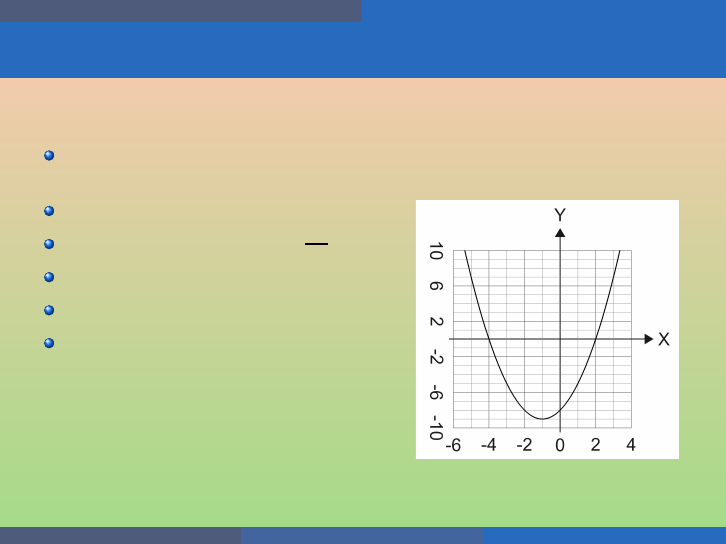
Quadratic Equations and Functions Graph Quadratic Functions Using Properties
Example
Graph f (x) = x
2
+ 2x − 8 by using its properties.
Opens up (a = 1 > 0);
Axis of symmetry: x = −
2
2·1
= −1;
Vertex (−1, − 9);
y-intercept (0, −8);
x-intercepts
x
2
+ 2x −8 = 0 ⇒ (x + 4)(x −2) =
0 ⇒ x = −4, x = 2
Points: (−4, 0) and (2, 0).
George Voutsadakis (LSSU) Intermediate Algebra August 2020 81 / 113
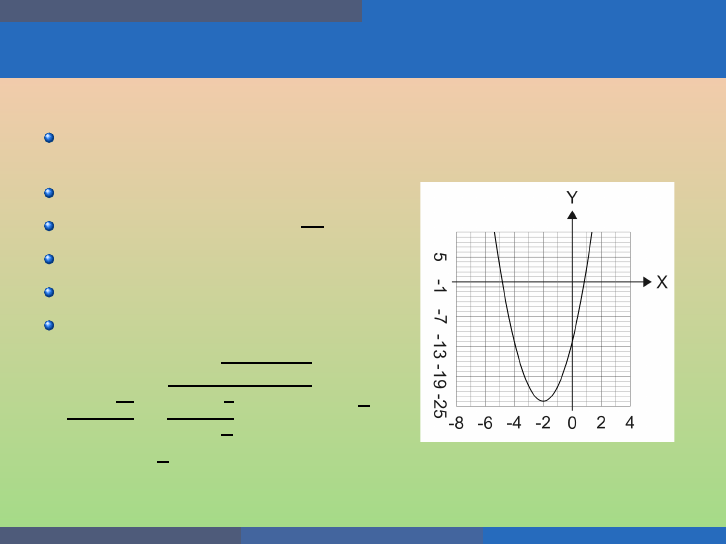
Quadratic Equations and Functions Graph Quadratic Functions Using Properties
Example
Graph f (x) = 3x
2
+ 12x − 12 by u sing its properties.
Opens up (a = 3 > 0);
Axis of symmetry x = −
12
2·3
= − 2;
Vertex (−2, − 24);
y-intercept (0, −12);
x-intercepts:
3x
2
+12x −12 = 0 ⇒ x
2
+4x −4 =
0 ⇒ x =
−4±
√
4
2
−4·1·(−4)
2·1
=
−4±
√
32
2
=
−4±4
√
2
2
= − 2 ± 2
√
2.
Points (−2 − 2
√
2, 0) and
(−1 + 2
√
2, 0).
George Voutsadakis (LSSU) Intermediate Algebra August 2020 82 / 113
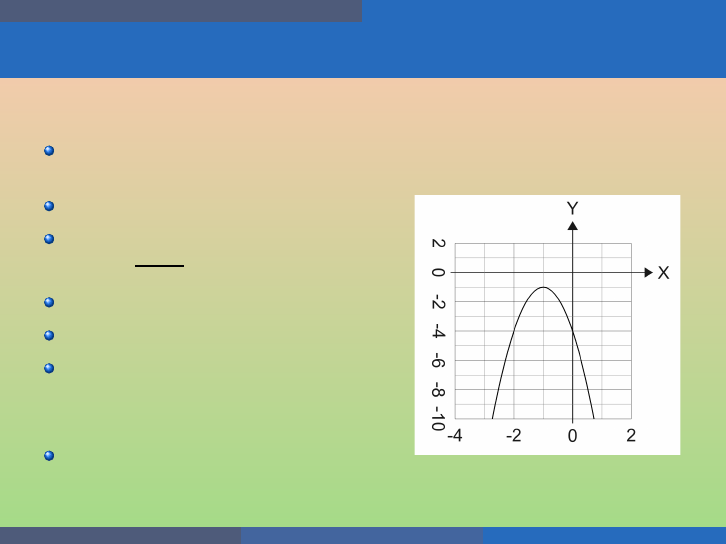
Quadratic Equations and Functions Graph Quadratic Functions Using Properties
Example
Graph f (x) = −3x
2
− 6x − 4 by using its properties.
Opens down (a = −3 < 0);
Axis of symmetry
x = −
−6
2·(−3)
= − 1;
Vertex (−1, − 1);
y-intercept (0, −4);
x-intercepts − 3x
2
− 6x − 4 = 0 ⇒
3x
2
+ 6x + 4 = 0 ⇒ D = b
2
−4ac =
36 − 4 · 3 · 4 = 36 − 48 = − 12 < 0
Need s ome more points: (−2, − 4)
George Voutsadakis (LSSU) Intermediate Algebra August 2020 83 / 113
Quadratic Equations and Functions Graph Quadratic Functions Using Properties
Solve Maximum and Minimum Applications
The y -coordinate of th e vertex of the graph of a quadratic function is:
The minimum value of the quadratic equ ation if the parabo la opens
upward;
The maximum value of the quad ratic equation if the parabola opens
downward.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 84 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Properties
Example
Find the maximum or minimum value of the quadratic fu n ction
f (x) = x
2
− 8x + 12.
The parabola opens up.
So the minimum value occurs at the vertex.
x = −
b
2a
= −
−8
2 · 1
= 4.
Thus, the minimum value is
y
min
= f (4) = 4
2
− 8 · 4 + 12 = 16 − 32 + 12 = − 4.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 85 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Properties
Physics: Maximum Height
The f ormula h(t) = −16t
2
+ v
0
t + h
0
gives the height in feet, h, of
an object sh ot upwards into the air from an initial height of h
0
feet,
with initial velocity, v
0
, after t seconds.
This formula is a quadratic function, so its graph is a parabola.
By solving for the coordinates of the vertex (t, h), we can find how
long it will ta ke the object to reach its maximum height.
Then we can calculate the maximum height.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 86 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Properties
Example
A path of a t oy rocket thrown upward from the ground at a rate of
208 ft/sec is modeled by the quadratic function
h(t) = −16t
2
+ 208t.
When will t h e rocket reach its maximum height? What will be the
maximum height?
The max imum height will be reached at
t = −
b
2a
= −
208
2 · (−16)
=
208
32
= 6.5 s ecs
The max imum height will be
h
max
= h(6.5) = − 16 · 6.5
2
+ 208 · 6.5 = − 676 + 1352 = 676 feet
George Voutsadakis (LSSU) Intermediate Algebra August 2020 87 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Transformations
We Shall Learn and Practice
Graph quadratic functions of th e form f (x) = x
2
+ k.
Graph quadratic functions of th e form f (x) = (x − h)
2
.
Graph quadratic functions of th e form f (x) = ax
2
.
Graph quadratic functions usi n g transformations.
Find a quadratic f u n ction from its graph.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 89 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Transformations
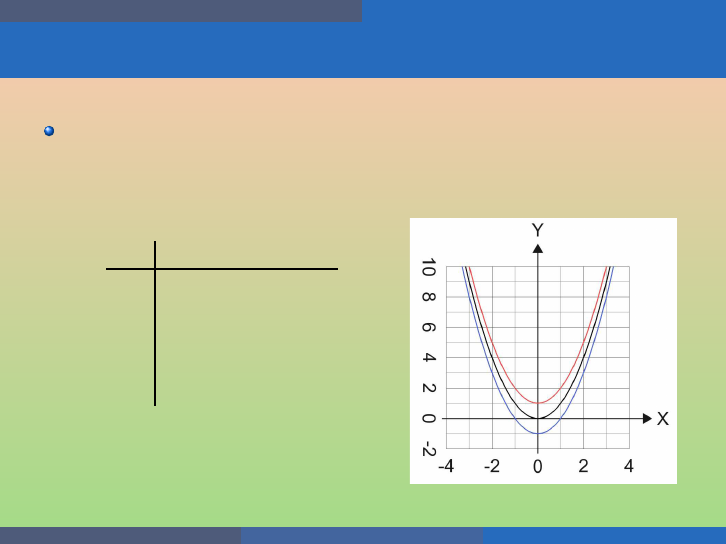
Quadratic Functions of the Form f (x ) = x
2
+ k
The graph of f (x) = x
2
+ k shifts the graph of f (x) = x
2
vertically k
units.
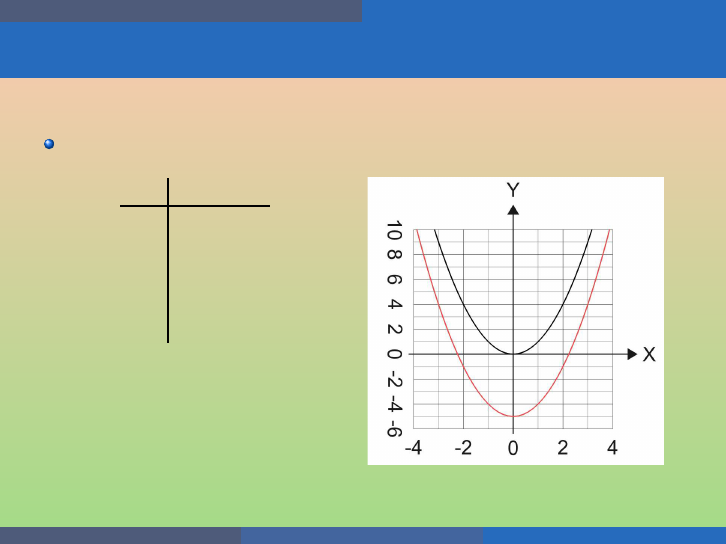
If k > 0, sh ift the parabola vertically up k units;
If k < 0, sh ift the parabola vertically down |k| units.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 90 / 113
Quadratic Equations and Functions Graph Quadratic Functions Using Transformations
Example
(a) G raph f (x) = x
2
, g(x) = x
2
+ 1, and h(x) = x
2
− 1 on the same
rectangular coordinat e system. (b) Describe what effect adding a
constant to the function has on the b asic parabola.
x f (x) g(x) h(x)
−2 4 5 3
−1 1 2 0
0 0 1 − 1
1 1 2 0
2 4 5 3
George Voutsadakis (LSSU) Intermediate Algebra August 2020 91 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Transformations
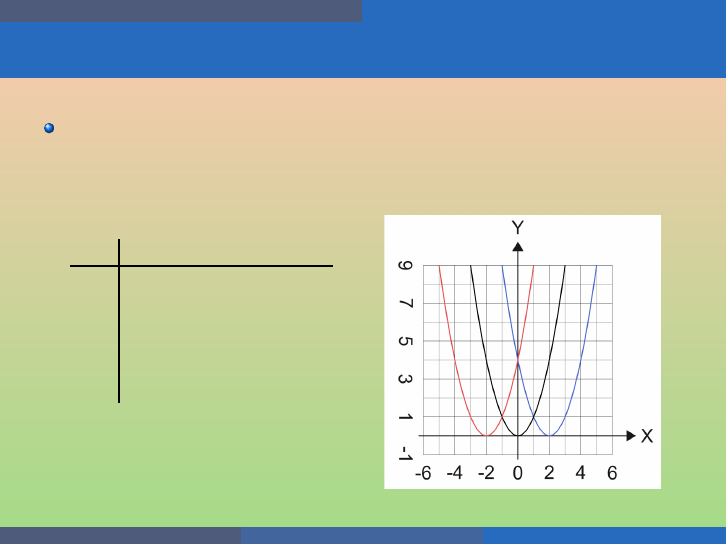
Quadratic Functions of the Form f (x ) = (x − h)
2
The graph of f (x) = (x − h)
2
shifts the graph of f (x) = x
2
hori zontally h units.
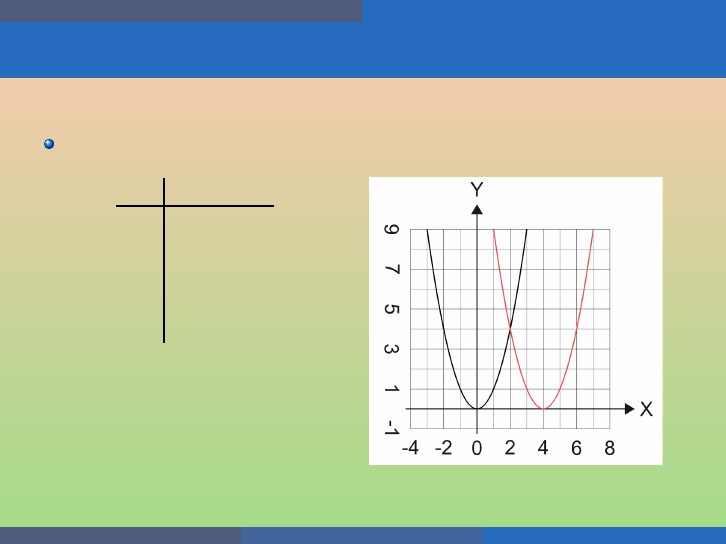
If h > 0, shift the parabola horizontally right h units;
If h < 0, shift the parabola horizontally left |h| units.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 93 / 113
Quadratic Equations and Functions Graph Quadratic Functions Using Transformations
Example
(a) G raph f (x) = x
2
, g(x) = (x + 2)
2
, and h(x) = (x − 2)
2
on the
same rectangular coordinate system. (b) Describe what effect adding
a constant to the f u n ction has on the ba sic parabola.
x f (x) g h
−2 4 (−4, 4) (0, 4)
−1 1 (−3, 1) (1, 1)
0 0 (−2, 0) (2, 0)
1 1 (−1, 1) (3, 1)
2 4 (0, 4) (4, 4)
George Voutsadakis (LSSU) Intermediate Algebra August 2020 94 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Transformations
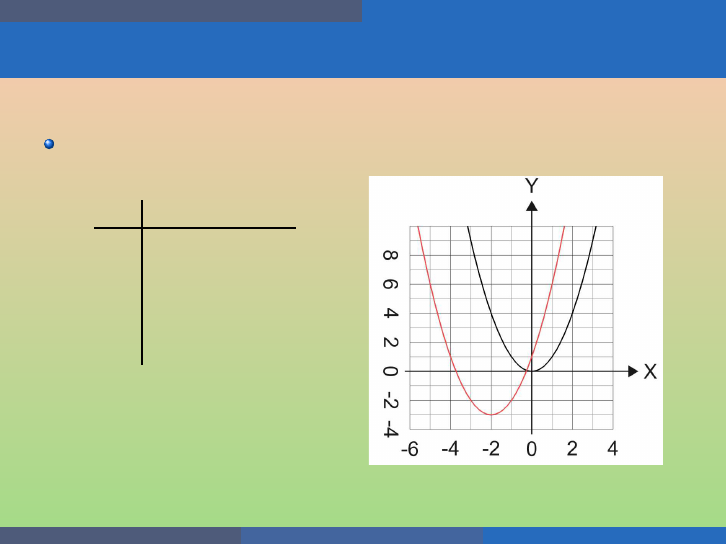
Quadratic Functions of the Form f (x ) = ax
2
The coefficient a in the function f (x) = ax
2
affects t h e graph of
f (x) = x
2
by stretching or compressing it.
If 0 < |a| < 1, the graph of f (x) = ax
2
will be “w ider” th an the graph
of f (x ) = x
2
;
If |a| > 1, the graph of f (x) = ax
2
will be “narrower” than the graph
of f (x ) = x
2
.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 97 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Transformations
Quadratic Functions Using Transformations
To graph using transformations, f ollow the steps:
Rewrite the function in f (x) = a(x − h)
2
+ k form by c ompleting the
square;
Graph the function using transformations.
To graph using properties, follow the steps:
Rewrite the function in f (x) = a(x − h)
2
+ k form;
Determine wh ether the parabola opens upward, a > 0, or downward,
a < 0;
Find the axis of symmetry, x = h;
Find the vertex, (h, k);
Find the y -inte rcep t (set x = 0);
Find the x-intercepts (set y = 0);
Graph the parabola.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 99 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Transformations
Example
Rewrite f (x) = −4x
2
− 8x + 1 in the f (x) = a(x − h)
2
+ k form by
completing the square.
f (x) = −4x
2
− 8x + 1
f (x) = −4(x
2
+ 2x) + 1
f (x) = −4(x
2
+ 2x + 1 − 1) + 1
f (x) = −4(x
2
+ 2x + 1) + 4 + 1
f (x) = −4(x + 1)
2
+ 5.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 100 / 113
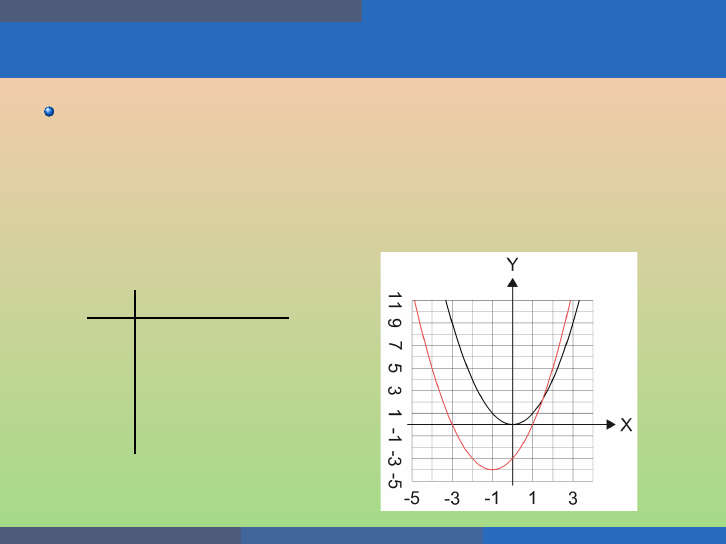
Quadratic Equations and Functions Graph Quadratic Functions Using Transformations
Example
Graph f (x) = x
2
+ 2x − 3 by using t ransformations.
We first transform into the form a(x − h)
2
+ k.
f (x) = x
2
+ 2x − 3
f (x) = x
2
+ 2x + 1 − 1 − 3
f (x) = (x + 1)
2
− 4
x x
2
f
−2 4 (−3, 0)
−1 1 (−2, − 3)
0 0 (−1, − 4)
1 1 (0, −3)
2 4 (1, 0)
George Voutsadakis (LSSU) Intermediate Algebra August 2020 101 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Transformations
Example
(a) R ewrit e f (x) = 3x
2
− 6x + 5 in f (x) = a(x −h)
2
+ k form and
(b) graph the function using properties.
(a)
f (x) = 3x
2
− 6x + 5
f (x) = 3(x
2
− 2x) + 5
f (x) = 3(x
2
− 2x + 1 − 1) + 5
f (x) = 3(x
2
− 2x + 1) − 3 + 5
f (x) = 3(x − 1)
2
+ 2.
On the next slide we graph the f u n ction using properties.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 102 / 113
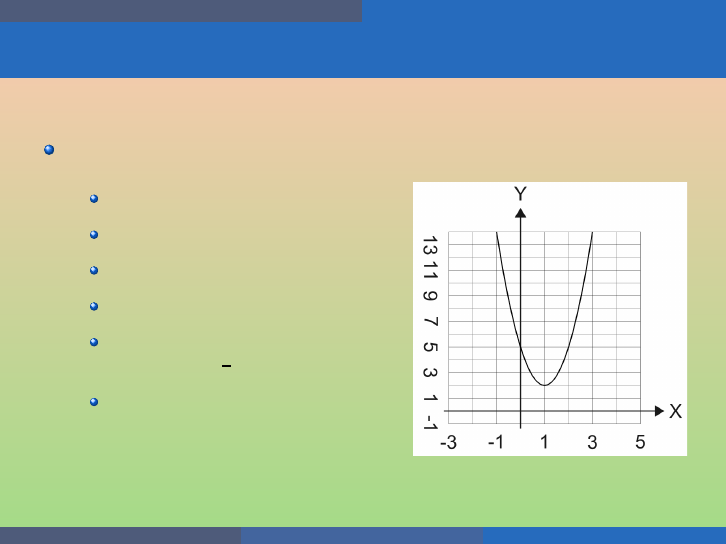
Quadratic Equations and Functions Graph Quadratic Functions Using Transformations
Example
We graph f (x) = 3(x − 1)
2
+ 2 using properties.
Opens up (a = 3 > 0);
Axis of symmetry x = 1;
Vertex (1, 2);
y-intercept (0, 5);
x-intercepts 3(x −1)
2
+ 2 = 0 ⇒
(x − 1)
2
= −
2
3
⇒ no solutions
Need some more points: (−1, 14)
George Voutsadakis (LSSU) Intermediate Algebra August 2020 103 / 113

Quadratic Equations and Functions Graph Quadratic Functions Using Transformations
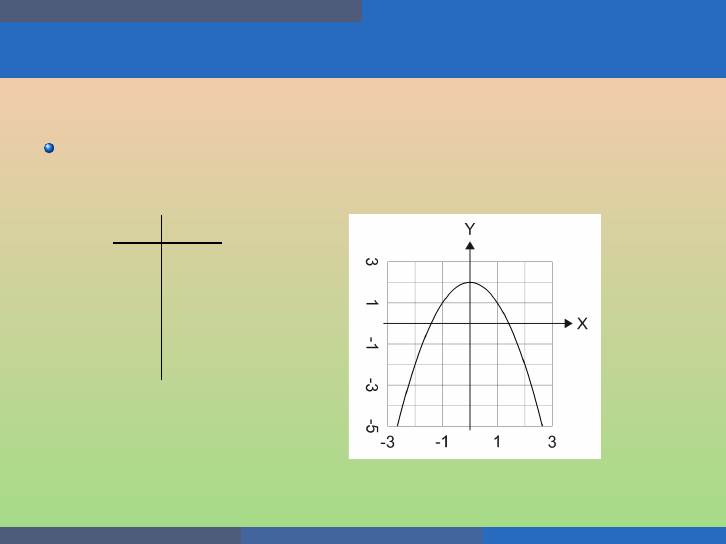
A Quadratic Function from its Graph
Write the q u adratic function in
f (x) = a(x − h)
2
+ k form
whose graph is shown.
Since the vertex is at
(h, k) = (3, −4), we get
f (x) = a(x − 3)
2
− 4.
Since (0, 5) is a point on the parabola, we must have
a(0 − 3)
2
− 4 = 5
9a − 4 = 5
9a = 9
a = 1.
Thus, the equat ion is f (x) = (x − 3)
2
− 4.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 104 / 113

Quadratic Equations and Functions Solve Quadratic Inequalities
Solve Quadratic Inequalities Graphically
A quadratic inequality is an inequality that contains a qua d ratic
expression.
The standard form of a quadratic inequality is written:
ax
2
+ bx + c < 0 ax
2
+ bx + c ≤ 0
ax
2
+ bx + c > 0 ax
2
+ bx + c ≥ 0
To solve a quadratic inequality graphical ly, follow the steps:
Write the quadratic inequa lity in standard form;
Graph the function f (x) = ax
2
+ bx + c;
Determine the solution from th e graph.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 107 / 113

Quadratic Equations and Functions Solve Quadratic Inequalities
Example
(a) Solve x
2
+ 2x − 8 < 0 graphically and (b) write the solution in
interval n ota tion.
Opens up (a = 1 > 0);
Axis of symmetry: x = −
2
2·1
= −1;
Vertex (−1, − 9);
y-intercept (0, −8);
x-intercepts
x
2
+ 2x −8 = 0 ⇒ (x + 4)(x −2) =
0 ⇒ x = − 4, x = 2
Points: (−4, 0) and (2, 0).
Thus for x
2
+ 2x − 8 to be negative, we must have −4 < x < 2.
In interval nota tion, the solution set is (−4, 2).
George Voutsadakis (LSSU) Intermediate Algebra August 2020 108 / 113
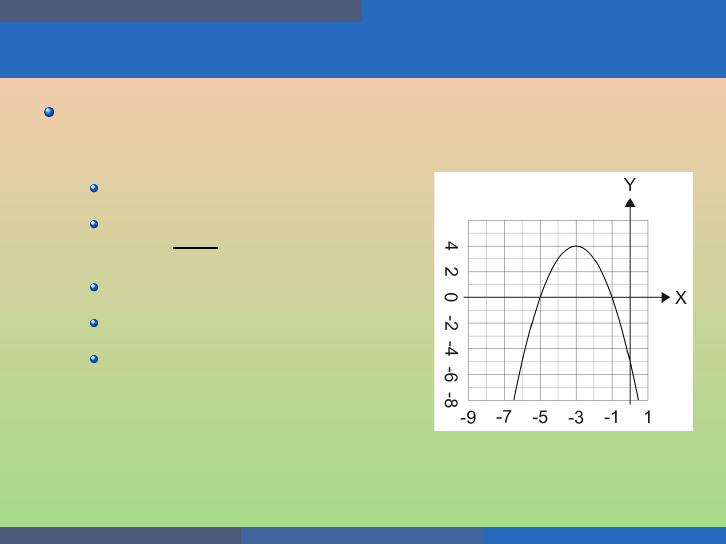
Quadratic Equations and Functions Solve Quadratic Inequalities
Example
(a) Solve −x
2
− 6x − 5 ≥ 0 graphically and (b) writ e the solution in
interval n ota tion.
Opens down (a = −1 < 0);
Axis of symmetry:
x = −
−6
2·(−1)
= − 3;
Vertex (−3, 4 );
y-intercept (0, −5);
x-intercepts − x
2
− 6x − 5 = 0 ⇒
x
2
+ 6x + 5 = 0 ⇒ (x + 1)(x + 5) =
0 ⇒ x = − 5, x = −1
Points: (−5, 0) and (−1, 0).
Thus for −x
2
− 6x − 5 to be ≥ 0, we must have −5 ≤ x ≤ −1.
In interval nota tion, the solution set is [−5, −1].
George Voutsadakis (LSSU) Intermediate Algebra August 2020 109 / 113

Quadratic Equations and Functions Solve Quadratic Inequalities
Solve Quadratic Inequalities Algebraically
To solve a quadratic inequality algebraically, follow the steps:
Write the quadratic inequa lity in standard form.
Determine the critical points - the solutions to the related qu adratic
equation.
Use the critical points to divide the n umber line into i n t e rvals .
Above the number line show the sign of each q uadratic expression using
test points from each interval substituted into the original inequality.
Determine the intervals where the inequality is correct and write the
solution in interval notation.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 110 / 113

Quadratic Equations and Functions Solve Quadratic Inequalities
Example
Solve x
2
+ 2x − 8 ≥ 0 algebraically. Write the solution in interval
notation.
We solve the equation x
2
+ 2x − 8 = 0 algebraically:
x
2
+ 2x − 8 = 0
(x + 4)(x − 2) = 0
x = −4 or x = 2.
Use these two point s to divide the line and then test the sign of the
expression x
2
+ 2x − 8 is each interval formed:
(−∞, −4) (−4, 2) (2, +∞)
x
2
+ 2x − 8 + − +
Since we want x
2
+ 2x − 8 to be ≥ 0, we get x ≤ −4 or x ≥ 2. In
interval n ota tion, the solution set is (−∞, −4] ∪ [2, +∞).
George Voutsadakis (LSSU) Intermediate Algebra August 2020 111 / 113
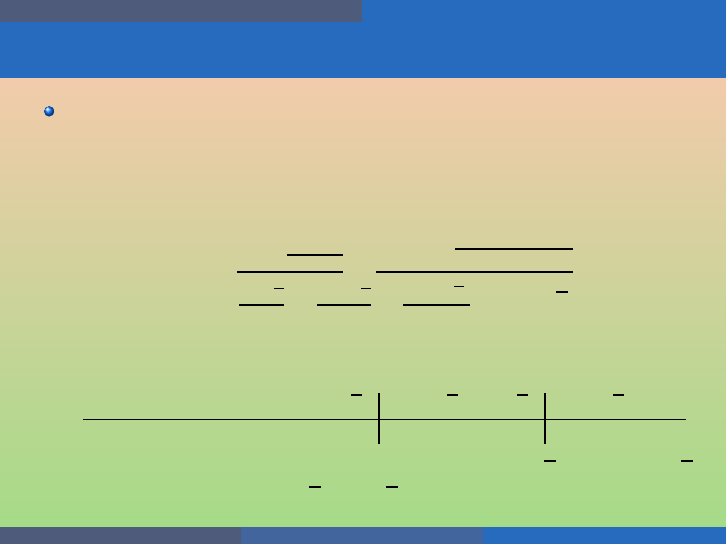
Quadratic Equations and Functions Solve Quadratic Inequalities
Example
Solve −x
2
+ 2x + 1 ≥ 0 algebraically. Write the solut ion in interval
notation.
We solve the equation −x
2
+ 2x + 1 = 0 algebraically:
− x
2
+ 2x + 1 = 0
x
2
− 2x − 1 = 0
x =
−b±
√
b
2
−4ac
2a
=
−(−2)±
√
(−2)
2
−4·1·(−1)
2·1
x =
2±
√
8
2
=
2±2
√
2
2
=
2(1±
√
2)
2
= 1 ±
√
2.
Use these two point s to divide the line and then test the sign of the
expression −x
2
+ 2x + 1 is each interval formed:
(−∞, 1 −
√
2) (1 −
√
2, 1 +
√
2) (1 +
√
2, +∞)
−x
2
+ 2x + 1 − + −
Since we want x
2
+ 2x − 8 to be ≥ 0, we get 1 −
√
2 ≤ x ≤ 1 +
√
2.
In interval nota tion [1 −
√
2, 1 +
√
2].
George Voutsadakis (LSSU) Intermediate Algebra August 2020 112 / 113

Quadratic Equations and Functions Solve Quadratic Inequalities
Example
Solve and write any soluti on in interval notation: (a)
−x
2
+ 2x − 4 ≤ 0 (b) −x
2
+ 2x − 4 ≥ 0.
We solve the equation −x
2
+ 2x − 4 = 0 algebraically:
− x
2
+ 2x − 4 = 0
x
2
− 2x + 4 = 0
D = b
2
− 4ac = (−2)
2
− 4 · 1 · 4 = − 12 < 0;
So, the equation has no real roots.
The line remains undivided. So we test the sign of the expression
−x
2
+ 2x − 4 in the only existing interval:
(−∞, +∞)
−x
2
+ 2x − 4 −
(a) Since we want − x
2
+ 2x − 4 to be ≤ 0, x must be i n (−∞, ∞).
(b) Since we want −x
2
+ 2x − 4 to be ≥ 0, the inequal ity has no
solutions.
George Voutsadakis (LSSU) Intermediate Algebra August 2020 113 / 113