
Figure 9.1 Several companies have patented contact lenses equipped with cameras, suggesting that they may be the future of
wearable camera technology. (credit: “intographics”/Pixabay)
Chapter Outline
9.1 Solve Quadratic Equations Using the Square Root Property
9.2 Solve Quadratic Equations by Completing the Square
9.3 Solve Quadratic Equations Using the Quadratic Formula
9.4 Solve Quadratic Equations in Quadratic Form
9.5 Solve Applications of Quadratic Equations
9.6 Graph Quadratic Functions Using Properties
9.7 Graph Quadratic Functions Using Transformations
9.8 Solve Quadratic Inequalities
Introduction
Blink your eyes. You’ve taken a photo. That’s what will happen if you are wearing a contact lens with a built-in camera.
Some of the same technology used to help doctors see inside the eye may someday be used to make cameras and other
devices. These technologies are being developed by biomedical engineers using many mathematical principles, including
an understanding of quadratic equations and functions. In this chapter, you will explore these kinds of equations and
learn to solve them in different ways. Then you will solve applications modeled by quadratics, graph them, and extend
your understanding to quadratic inequalities.
9.1
Solve Quadratic Equations Using the Square Root Property
Learning Objectives
By the end of this section, you will be able to:
Solve quadratic equations of the form
ax
2
= k
using the Square Root Property
Solve quadratic equations of the form
a(x – h)
2
= k
using the Square Root Property
Be Prepared!
Before you get started, take this readiness quiz.
1. Simplify:
128.
If you missed this problem, review Example 8.13.
2. Simplify:
32
5
.
QUADRATIC EQUATIONS AND FUNCTIONS
9
Chapter 9 Quadratic Equations and Functions 859
If you missed this problem, review Example 8.50.
3. Factor:
9x
2
− 12x + 4
.
If you missed this problem, review Example 6.23.
A quadratic equation is an equation of the form ax
2
+ bx + c = 0, where
a ≠ 0
. Quadratic equations differ from linear
equations by including a quadratic term with the variable raised to the second power of the form ax
2
. We use different
methods to solve quadratic equations than linear equations, because just adding, subtracting, multiplying, and dividing
terms will not isolate the variable.
We have seen that some quadratic equations can be solved by factoring. In this chapter, we will learn three other methods
to use in case a quadratic equation cannot be factored.
Solve Quadratic Equations of the form
ax
2
= k
using the Square Root Property
We have already solved some quadratic equations by factoring. Let’s review how we used factoring to solve the quadratic
equation x
2
= 9.
Put the equation in standard form.
Factor the diffe ence of squares.
x
2
= 9
x
2
− 9 = 0
(
x − 3
)(
x + 3
)
= 0
Use the Zero Product Property.
Solve each equation.
x − 3 = 0 x − 3 = 0
x = 3 x = −3
We can easily use factoring to find the solutions of similar equations, like x
2
= 16 and x
2
= 25, because 16 and 25 are perfect
squares. In each case, we would get two solutions,
x = 4, x = −4
and
x = 5, x = −5.
But what happens when we have an equation like x
2
= 7? Since 7 is not a perfect square, we cannot solve the equation by
factoring.
Previously we learned that since 169 is the square of 13, we can also say that 13 is a square root of 169. Also, (−13)
2
= 169,
so −13 is also a square root of 169. Therefore, both 13 and −13 are square roots of 169. So, every positive number has two
square roots—one positive and one negative. We earlier defined the square root of a number in this way:
If n
2
= m, then n is a square root of m.
Since these equations are all of the form x
2
= k, the square root definition tells us the solutions are the two square roots
of k. This leads to the Square Root Property.
Square Root Property
If x
2
= k, then
x = k or x = − k or x = ± k.
Notice that the Square Root Property gives two solutions to an equation of the form x
2
= k, the principal square root of
k
and its opposite. We could also write the solution as
x = ± k.
We read this as x equals positive or negative the square
root of k.
Now we will solve the equation x
2
= 9 again, this time using the Square Root Property.
Use the Square Root Property.
x
2
= 9
x = ± 9
x = ±3
So x = 3 or x = −3.
What happens when the constant is not a perfect square? Let’s use the Square Root Property to solve the equation x
2
= 7.
x
2
= 7
Use the Square Root Property. x = 7, x = − 7
We cannot simplify
7
, so we leave the answer as a radical.
EXAMPLE 9.1 HOW TO SOLVE A QUADRATIC EQUATION OF THE FORM
AX
2
=
K
USING THE SQUARE ROOT
PROPERTY
Solve:
x
2
− 50 = 0
.
860 Chapter 9 Quadratic Equations and Functions
This OpenStax book is available for free at http://cnx.org/content/col12119/1.3

Solution
TRY IT : :
9.1
Solve:
x
2
− 48 = 0.
TRY IT : :
9.2
Solve:
y
2
− 27 = 0.
The steps to take to use the Square Root Property to solve a quadratic equation are listed here.
In order to use the Square Root Property, the coefficient of the variable term must equal one. In the next example, we
must divide both sides of the equation by the coefficient 3 before using the Square Root Property.
EXAMPLE 9.2
Solve:
3z
2
= 108.
HOW TO : : SOLVE A QUADRATIC EQUATION USING THE SQUARE ROOT PROPERTY.
Isolate the quadratic term and make its coefficient one.
Use Square Root Property.
Simplify the radical.
Check the solutions.
Step 1.
Step 2.
Step 3.
Step 4.
Chapter 9 Quadratic Equations and Functions 861
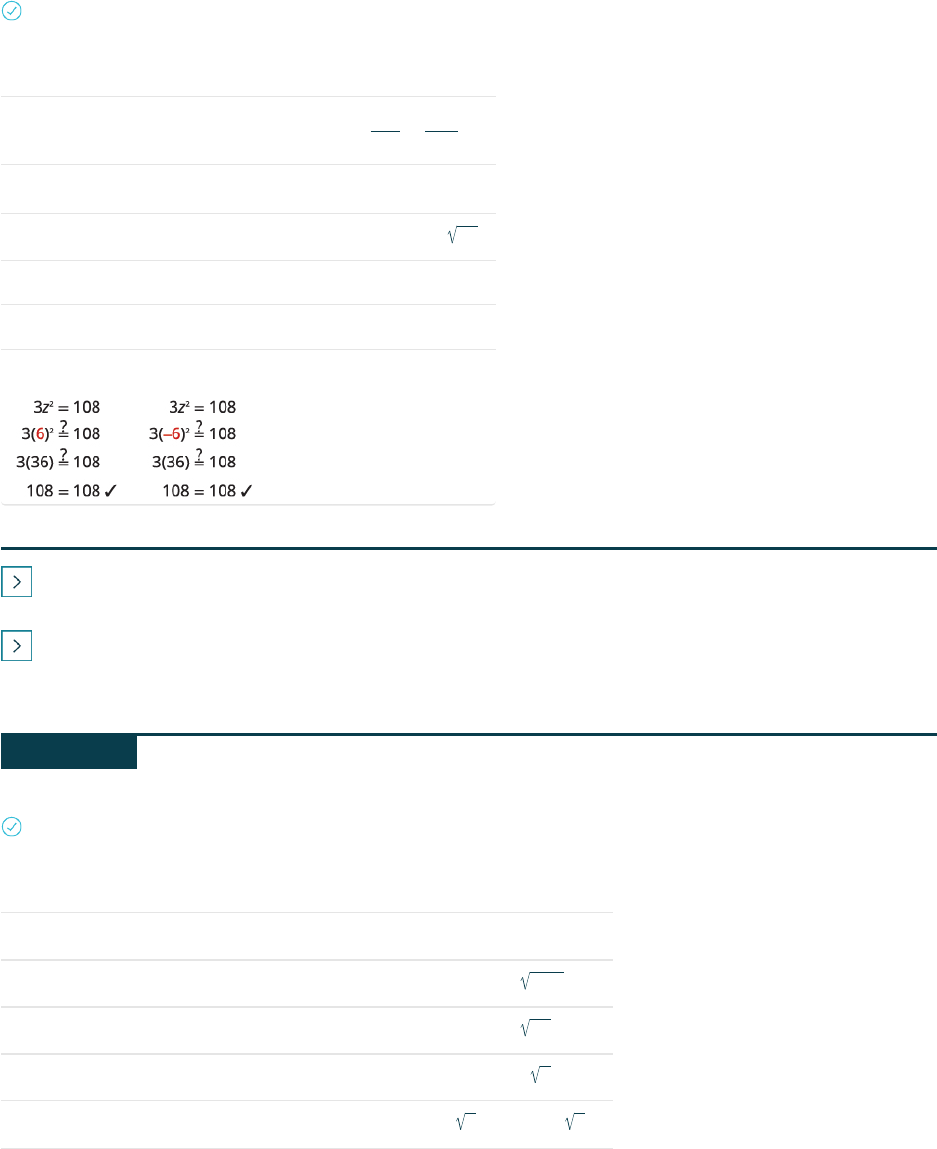
Solution
3z
2
= 108
The quadratic term is isolated.
Divide by 3 to make its coefficient 1.
3z
2
3
=
108
3
Simplify.
z
2
= 36
Use the Square Root Property.
z = ± 36
Simplify the radical.
z = ± 6
Rewrite to show two solutions.
z = 6, z = −6
Check the solutions:
TRY IT : :
9.3
Solve:
2x
2
= 98.
TRY IT : :
9.4
Solve:
5m
2
= 80.
The Square Root Property states ‘If
x
2
= k
,’ What will happen if
k < 0?
This will be the case in the next example.
EXAMPLE 9.3
Solve:
x
2
+ 72 = 0
.
Solution
x
2
+ 72 = 0
Isolate the quadratic term.
x
2
= −72
Use the Square Root Property.
x = ± −72
Simplify using complex numbers.
x = ± 72 i
Simplify the radical.
x = ± 6 2 i
Rewrite to show two solutions.
x = 6 2 i, x = −6 2 i
862 Chapter 9 Quadratic Equations and Functions
This OpenStax book is available for free at http://cnx.org/content/col12119/1.3

Check the solutions:
TRY IT : :
9.5
Solve:
c
2
+ 12 = 0.
TRY IT : :
9.6
Solve:
q
2
+ 24 = 0
.
Our method also works when fractions occur in the equation, we solve as any equation with fractions. In the next example,
we first isolate the quadratic term, and then make the coefficient equal to one.
EXAMPLE 9.4
Solve:
2
3
u
2
+ 5 = 17.
Solution
2
3
u
2
+ 5 = 17
Isolate the quadratic term.
Multiply by
3
2
to make the coefficient 1.
Simplify.
Use the Square Root Property.
Simplify the radical.
Simplify.
Rewrite to show two solutions.
Check:
TRY IT : :
9.7
Solve:
1
2
x
2
+ 4 = 24.
Chapter 9 Quadratic Equations and Functions 863
TRY IT : :
9.8
Solve:
3
4
y
2
− 3 = 18.
The solutions to some equations may have fractions inside the radicals. When this happens, we must rationalize the
denominator.
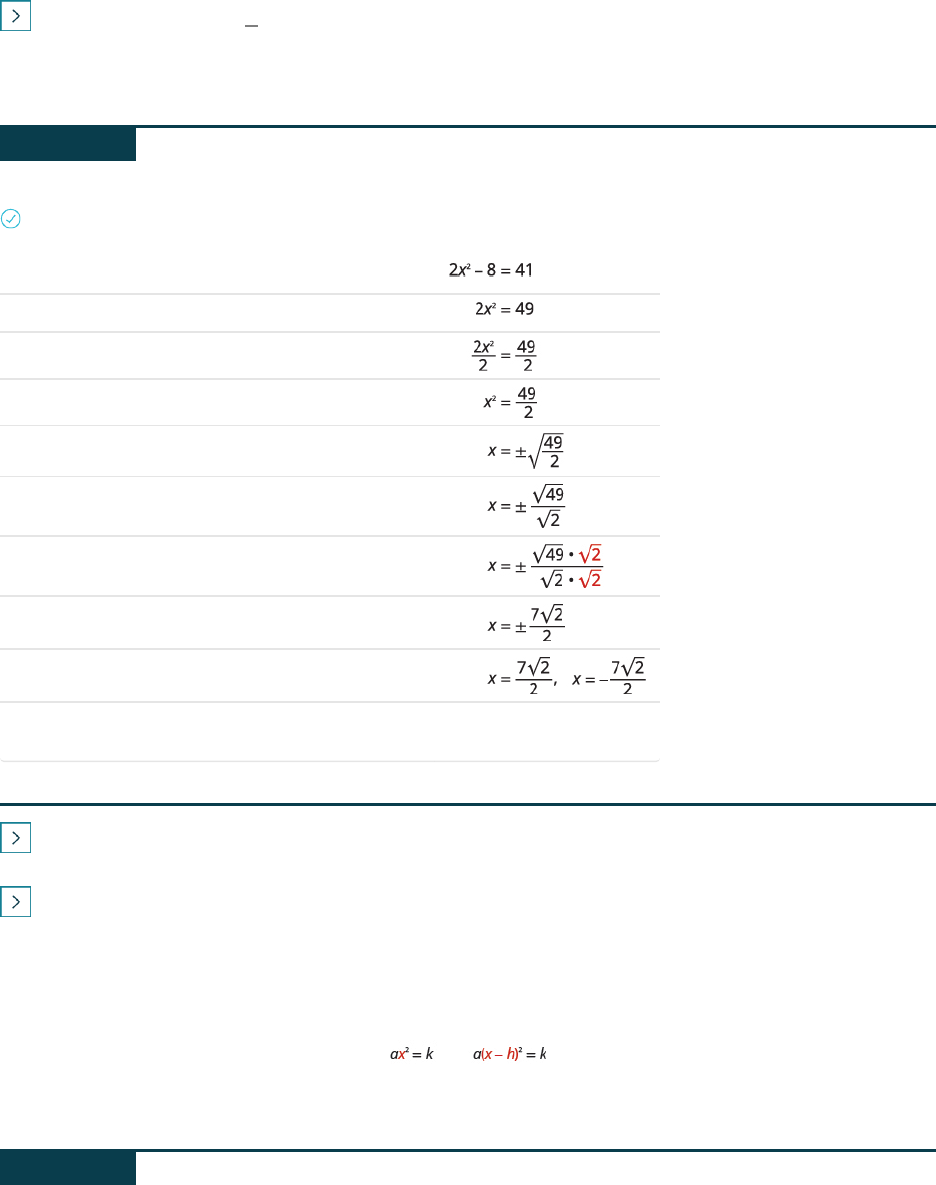
EXAMPLE 9.5
Solve:
2x
2
− 8 = 41
.
Solution
Isolate the quadratic term.
Divide by
2
to make the coefficient 1.
Simplify.
Use the Square Root Property.
Rewrite the radical as a fraction of square roots.
Rationalize the denominator.
Simplify.
Rewrite to show two solutions.
Check:
We leave the check for you.
TRY IT : :
9.9
Solve:
5r
2
− 2 = 34.
TRY IT : :
9.10
Solve:
3t
2
+ 6 = 70.
Solve Quadratic Equations of the Form a(x − h)
2
= k Using the Square Root Property
We can use the Square Root Property to solve an equation of the form a(x − h)
2
= k as well. Notice that the quadratic term,
x, in the original form ax
2
= k is replaced with (x − h).
The first step, like before, is to isolate the term that has the variable squared. In this case, a binomial is being squared.
Once the binomial is isolated, by dividing each side by the coefficient of a, then the Square Root Property can be used on
(x − h)
2
.
EXAMPLE 9.6
Solve:
4
⎛
⎝
y − 7
⎞
⎠
2
= 48.
864 Chapter 9 Quadratic Equations and Functions
This OpenStax book is available for free at http://cnx.org/content/col12119/1.3

Solution
4
⎛
⎝
y − 7
⎞
⎠
2
= 48
Divide both sides by the coefficient 4.
⎛
⎝
y − 7
⎞
⎠
2
= 12
Use the Square Root Property on the binomial
y − 7 = ± 12
Simplify the radical.
y − 7 = ± 2 3
Solve for
y.
y = 7 ± 2 3
Rewrite to show two solutions.
y = 7 + 2 3,
y = 7 − 2 3
Check:
TRY IT : :
9.11
Solve:
3
(
a − 3
)
2
= 54.
TRY IT : :
9.12
Solve:
2
(
b + 2
)
2
= 80.
Remember when we take the square root of a fraction, we can take the square root of the numerator and denominator
separately.
EXAMPLE 9.7
Solve:
⎛
⎝
x −
1
3
⎞
⎠
2
=
5
9
.
Chapter 9 Quadratic Equations and Functions 865

Solution
⎛
⎝
x −
1
3
⎞
⎠
2
=
5
9
Use the Square Root Property. x −
1
3
= ±
5
9
Rewrite the radical as a fraction of square roots. x −
1
3
= ±
5
9
Simplify the radical. x −
1
3
= ±
5
3
Solve for x. x =
1
3
±
5
3
Rewrite to show two solutions. x =
1
3
+
5
3
, x =
1
3
−
5
3
Check:
We leave the check for you.
TRY IT : :
9.13
Solve:
⎛
⎝
x −
1
2
⎞
⎠
2
=
5
4
.
TRY IT : :
9.14
Solve:
⎛
⎝
y +
3
4
⎞
⎠
2
=
7
16
.
We will start the solution to the next example by isolating the binomial term.
EXAMPLE 9.8
Solve:
2
(
x − 2
)
2
+ 3 = 57.
Solution
Subtract 3 from both sides to isolate
the binomial term.
Divide both sides by 2.
Use the Square Root Property.
Simplify the radical.
Solve for x.
2
(
x − 2
)
2
+ 3 = 57
2
(
x − 2
)
2
= 54
(
x − 2
)
2
= 27
x − 2 = ± 27
x − 2 = ±3 3
x = 2 ± 3 3
Rewrite to show two solutions. x = 2 + 3 3, x = 2 − 3 3
Check:
We leave the check for you.
TRY IT : :
9.15
Solve:
5
(
a − 5
)
2
+ 4 = 104
.
TRY IT : :
9.16
Solve:
3
(
b + 3
)
2
− 8 = 88.
Sometimes the solutions are complex numbers.
EXAMPLE 9.9
866 Chapter 9 Quadratic Equations and Functions
This OpenStax book is available for free at http://cnx.org/content/col12119/1.3
Solve:
(
2x − 3
)
2
= −12.
Solution
Use the Square Root Property.
Simplify the radical.
Add 3 to both sides.
Divide both sides by 2.
Rewrite in standard form.
Simplify.
(
2x − 3
)
2
= −12
2x − 3 = ± −12
2x − 3 = ±2 3 i
2x = 3 ± 2 3 i
x =
3 ± 2 3 i
2
x =
3
2
±
2 3 i
2
x =
3
2
± 3 i
Rewrite to show two solutions. x =
3
2
+ 3 i, x =
3
2
− 3 i
Check:
We leave the check for you.
TRY IT : :
9.17
Solve:
(
3r + 4
)
2
= −8.
TRY IT : :
9.18
Solve:
(
2t − 8
)
2
= −10.
The left sides of the equations in the next two examples do not seem to be of the form a(x − h)
2
. But they are perfect
square trinomials, so we will factor to put them in the form we need.
EXAMPLE 9.10
Solve:
4n
2
+ 4n + 1 = 16
.
Solution
We notice the left side of the equation is a perfect square trinomial. We will factor it first.
4n
2
+ 4n + 1 = 16
Factor the perfect square trinomial.
(
2n + 1
)
2
= 16
Use the Square Root Property.
2
n + 1 = ± 16
Simplify the radical.
2
n + 1 = ± 4
Solve for
n
.
2
n = −1 ± 4
Divide each side by 2.
2n
2
=
−1 ± 4
2
n =
−1 ± 4
2
Rewrite to show two solutions.
n =
−1 + 4
2
,
n =
−1 − 4
2
Simplify each equation.
n =
3
2
,
n = −
5
2
Chapter 9 Quadratic Equations and Functions 867
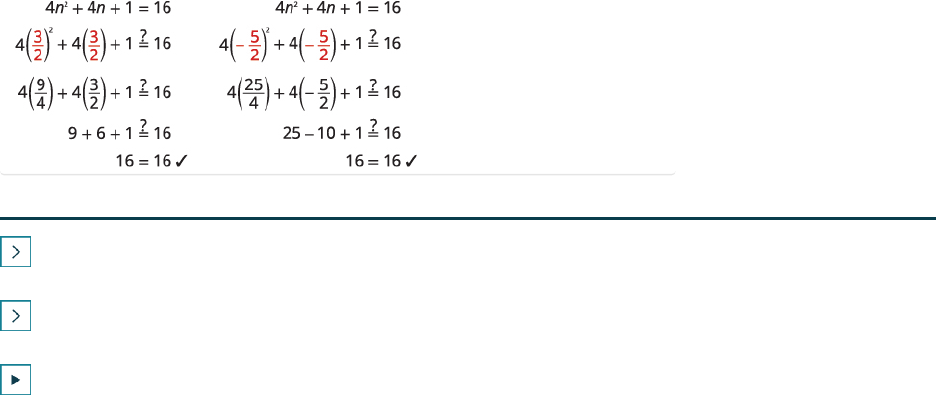
Check:
TRY IT : :
9.19
Solve:
9m
2
− 12m + 4 = 25.
TRY IT : :
9.20
Solve:
16
n
2
+ 40n + 25 = 4
.
MEDIA : :
Access this online resource for additional instruction and practice with using the Square Root Property to solve
quadratic equations.
• Solving Quadratic Equations: The Square Root Property (https://openstax.org/l/37SqRtProp1)
• Using the Square Root Property to Solve Quadratic Equations (https://openstax.org/l/37SqRtProp2)
868 Chapter 9 Quadratic Equations and Functions
This OpenStax book is available for free at http://cnx.org/content/col12119/1.3
Practice Makes Perfect
Solve Quadratic Equations of the Form ax
2
= k Using the Square Root Property
In the following exercises, solve each equation.
1.
a
2
= 49
2.
b
2
= 144
3.
r
2
− 24 = 0
4.
t
2
− 75 = 0
5.
u
2
− 300 = 0
6.
v
2
− 80 = 0
7.
4
m
2
= 36
8.
3
n
2
= 48
9.
4
3
x
2
= 48
10.
5
3
y
2
= 60
11.
x
2
+ 25 = 0
12.
y
2
+ 64 = 0
13.
x
2
+ 63 = 0
14.
y
2
+ 45 = 0
15.
4
3
x
2
+ 2 = 110
16.
2
3
y
2
− 8 = −2
17.
2
5
a
2
+ 3 = 11
18.
3
2
b
2
− 7 = 41
19.
7p
2
+ 10 = 26
20.
2
q
2
+ 5 = 30
21.
5y
2
− 7 = 25
22.
3x
2
− 8 = 46
Solve Quadratic Equations of the Form a(x − h)
2
= k Using the Square Root Property
In the following exercises, solve each equation.
23.
(
u − 6
)
2
= 64
24.
(
v + 10
)
2
= 121
25.
(
m − 6
)
2
= 20
26.
(
n + 5
)
2
= 32
27.
⎛
⎝
r −
1
2
⎞
⎠
2
=
3
4
28.
⎛
⎝
x +
1
5
⎞
⎠
2
=
7
25
29.
⎛
⎝
y +
2
3
⎞
⎠
2
=
8
81
30.
⎛
⎝
t −
5
6
⎞
⎠
2
=
11
25
31.
(
a − 7
)
2
+ 5 = 55
32.
(
b − 1
)
2
− 9 = 39
33.
4
(
x + 3
)
2
− 5 = 27
34.
5
(
x + 3
)
2
− 7 = 68
35.
(
5
c + 1
)
2
= −27
36.
(
8
d − 6
)
2
= −24
37.
(
4x − 3
)
2
+ 11 = −17
38.
⎛
⎝
2y + 1
⎞
⎠
2
− 5 = −23
39.
m
2
− 4m + 4 = 8
40.
n
2
+ 8n + 16 = 27
41.
x
2
− 6x + 9 = 12
42.
y
2
+ 12y + 36 = 32
43.
25x
2
− 30x + 9 = 36
44.
9y
2
+ 12y + 4 = 9
45.
36x
2
− 24x + 4 = 81
46.
64x
2
+ 144x + 81 = 25
9.1 EXERCISES
Chapter 9 Quadratic Equations and Functions 869
Mixed Practice
In the following exercises, solve using the Square Root Property.
47.
2r
2
= 32
48.
4t
2
= 16
49.
(
a − 4
)
2
= 28
50.
(
b + 7
)
2
= 8
51.
9w
2
− 24w + 16 = 1
52.
4z
2
+ 4z + 1 = 49
53.
a
2
− 18 = 0
54.
b
2
− 108 = 0
55.
⎛
⎝
p −
1
3
⎞
⎠
2
=
7
9
56.
⎛
⎝
q −
3
5
⎞
⎠
2
=
3
4
57.
m
2
+ 12 = 0
58.
n
2
+ 48 = 0.
59.
u
2
− 14
u + 49 = 72
60.
v
2
+ 18
v + 81 = 50
61.
(
m − 4
)
2
+ 3 = 15
62.
(
n − 7
)
2
− 8 = 64
63.
(
x + 5
)
2
= 4
64.
⎛
⎝
y − 4
⎞
⎠
2
= 64
65.
6c
2
+ 4 = 29
66.
2d
2
− 4 = 77
67.
(
x − 6
)
2
+ 7 = 3
68.
⎛
⎝
y − 4
⎞
⎠
2
+ 10 = 9
Writing Exercises
69. In your own words, explain the Square Root
Property.
70. In your own words, explain how to use the Square
Root Property to solve the quadratic equation
(
x + 2
)
2
= 16
.
Self Check
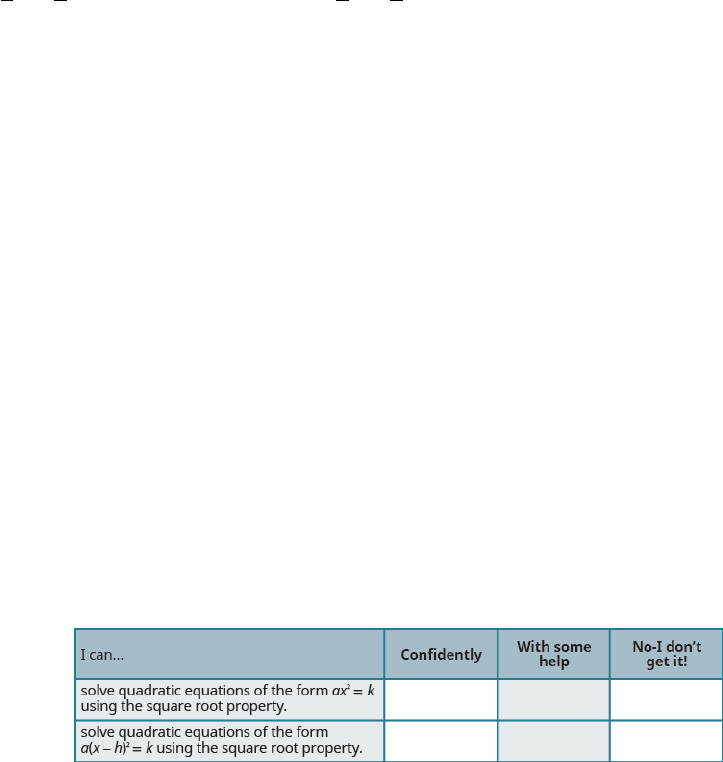
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
Choose how would you respond to the statement “I can solve quadratic equations of the form a times the square of x minus h
equals k using the Square Root Property.” “Confidently,” “with some help,” or “No, I don’t get it.”
ⓑ If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you
can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success.
In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on.
Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math
tutors are available? Can your study skills be improved?
…no - I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be
870 Chapter 9 Quadratic Equations and Functions
This OpenStax book is available for free at http://cnx.org/content/col12119/1.3
overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you
the help you need.
Chapter 9 Quadratic Equations and Functions 871
