Calculus 2
Lia Vas
Derivatives of Exponential and Logarithmic Functions.
Logarithmic Differentiation
Derivative of exponential functions. The natural exponential function can be considered as
“the easiest function in Calculus courses” since
the derivative of e
x
is e
x
.
General Exponential Function a
x
. Assuming the formula for e
x
, you can obtain the formula
for the derivative of any other base a > 0 by noting that y = a
x
is equal to e
ln a
x
= e
x ln a
. Use chain
rule and the formula for derivative of e
x
to obtain that y
0
= e
x ln a
ln a = a
x
ln a. Thus
the derivative of a
x
is a
x
ln a.
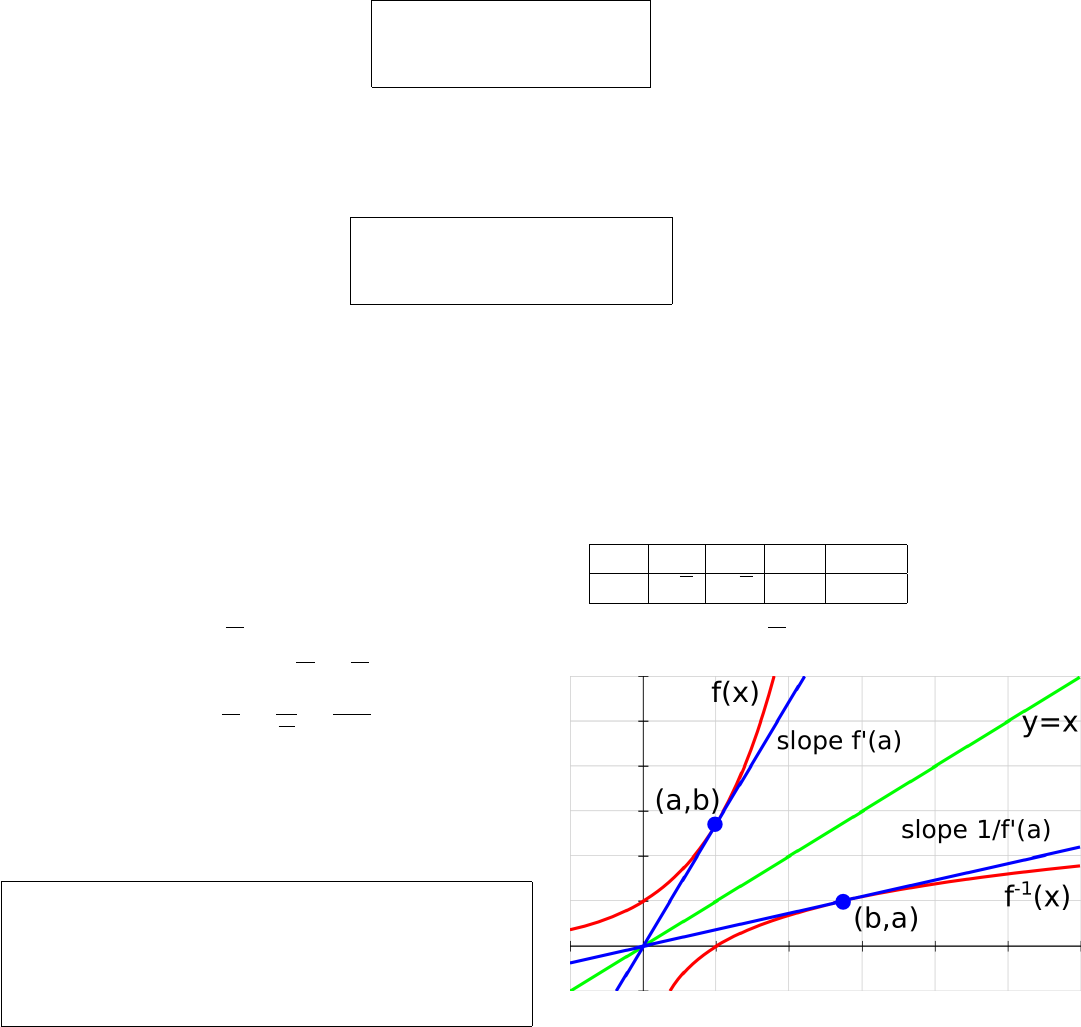
Derivative of the inverse function. If f (x) is a one-to-one function (i.e. the graph of f(x)
passes the horizontal line test), then f(x) has the inverse function f
−1
(x). Recall that f and f
−1
are
related by the following formulas
y = f
−1
(x) ⇐⇒ x = f(y).
Also, recall that the graphs of f
−1
(x) and f (x) are symmetrical with respect to line y = x.
Some pairs of inverse functions you encountered before are given in the following table where n
is a positive integer and a is a positive real number.
f x
2
x
n
e
x
a
x
f
−1
√
x
n
√
x ln x log
a
x
With y = f
−1
(x),
dy
dx
denotes the derivative of f
−1
and since x = f(y),
dx
dy
denotes the derivative
of f. Since the reciprocal of
dy
dx
is
dx
dy
we have that
(f
−1
)
0
(x) =
dy
dx
=
1
dx
dy
=
1
f
0
(y)
.
Thus, the derivative of the inverse function of
f is reciprocal of the derivative of f.
Graphically, this rule means that
The slope of the tangent to f
−1
(x) at point (b, a)
is reciprocal to
the slope of the tangent to f(x) at point (a, b).
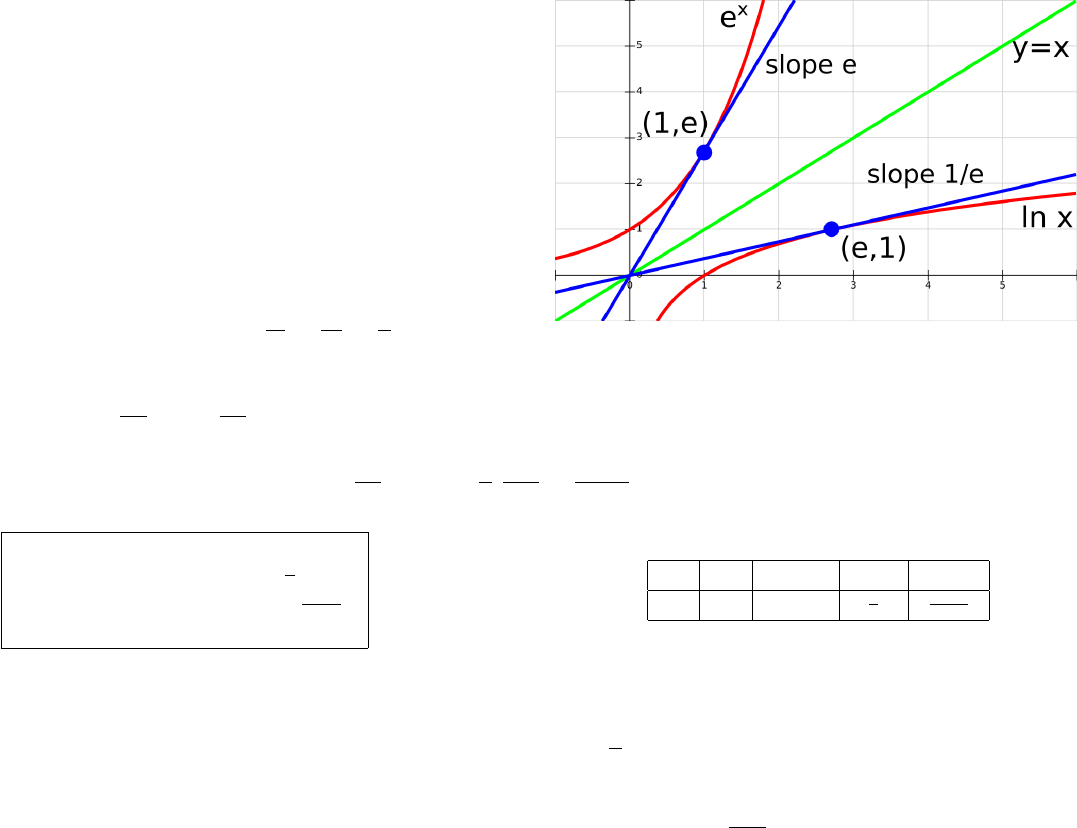
Logarithmic function and their derivatives.
Recall that the function log
a
x is the inverse
function of a
x
: thus log
a
x = y ⇔ a
y
= x.
If a = e, the notation ln x is short for log
e
x
and the function ln x is called the natural loga-
rithm.
The derivative of y = ln x can be obtained
from derivative of the inverse function x = e
y
.
Note that the derivative x
0
of x = e
y
is x
0
= e
y
=
x and consider the reciprocal:
y = ln x ⇒ y
0
=
1
x
0
=
1
e
y
=
1
x
.
The derivative of logarithmic function of any base can be obtained converting log
a
to ln as
y = log
a
x =
ln x
ln a
= ln x
1
ln a
and using the formula for derivative of ln x. So we have
d
dx
log
a
x =
1
x
1
ln a
=
1
x ln a
.
The derivative of ln x is
1
x
and
the derivative of log
a
x is
1
x ln a
.
To summarize,
y e
x
a
x
ln x log
a
x
y
0
e
x
a
x
ln a
1
x
1
x ln a
Besides two logarithm rules we used above, we recall another two rules which can also be useful.
log
a
(xy) = log
a
x + log
a
y log
a
(
x
y
) = log
a
x − log
a
y
log
a
(x
r
) = r log
a
x log
a
x =
ln x
ln a
Logarithmic Differentiation.
Assume that the function has the form y = f(x)
g(x)
where both f and g are non-constant
functions. Although this function is not implicit, it does not fall under any of the forms for which
we developed differentiation formulas so far. This is because of the following.
• In order to use the power rule, the exponent needs to be constant.
• In order to use the exponential function differentiation formula, the base needs to be constant.
Thus, no differentiation rule covers the case y = f(x)
g(x)
. These functions sill can be differentiated
by using the method known as the logarithmic differentiation.
To differentiate a function of the form y = f (x)
g(x)
follow the steps of the logarithmic differenti-
ation below.
1. Take ln of both sides of the equation y = f (x)
g(x)
.

2. Rewrite the right side ln f(x)
g(x)
as g(x) · ln(f (x)).
3. Differentiate both sides.
4. Solve the resulting equation for y
0
.
Example 1. Find the derivative of y = x
x
.
Solution. Follow the steps of the logarithmic differentiation.
1. First take ln of each side to get ln y = ln x
x
.
2. Rewrite the right side as x ln x to get ln y = x ln x.
3. Then differentiate both sides. Use the chain rule for the left side noting that the derivative of
the inner function y is y
0
. Use the product rule for the right side. Obtain
1
y
y
0
= ln x +
1
x
x.
4. Multiply both sides with y to solve for y
0
and get y
0
= (ln x + 1)y. Finally, recall that y = x
x
to get the derivative solely in terms of x as
y
0
= (ln x + 1)x
x
.
Practice Problems:
1. Find the derivatives of the following functions. In parts (g), (h) and (p) a and b are arbitrary
constants.
(a) y = (x
2
+ 1)e
3x
(b) y = e
x
2
+3x
(c) y =
e
2x
+e
−2x
x
2
(d) y = 3
x
2
+3x
(e) y = x 5
3x
(f) y =
3
x
−3
−x
2
(g) y = xe
ax
2
+1
(h) y =
√
1 + ae
x
(i) y = (2x + e
x
2
)
4
(j) y = ln(x
2
+ 2x) (k) y = log
2
(3x + 4) (l) y = x ln(x
2
+ 1)
(m) y = log
3
(x
2
+ 5) (n) y =
x ln x
x
2
+1
(o) y = ln(x + 5e
3x
)
(p) y = ax ln(x
2
+ b
2
) (q) y = (3x)
5x
(r) y = x
ln x
(s) y = (ln x)
x
(t) y = (3x + 2)
2x−1
2. Solve the equations for x:
(a) 2
x−1
= 5 (b) 3
2x+3
= 7
(c) e
3x+4
= 2 (d) (3.2)
x
= 64.6
(e) log
3
(x + 4) = 1 (f) log
5
(x
2
+ 9) = 2
(g) ln(ln x) = 0 (h) ln(x + 2) + ln e
3
= 7

3. This problem deals with functions called the hyperbolic sine and the hyperbolic cosine. These
functions occur in the solutions of some differential equations that appear in electromagnetic
theory, heat transfer, fluid dynamics, and special relativity. Hyperbolic sine and cosine are
defined as follows.
sinh x =
e
x
− e
−x
2
and cosh x =
e
x
+ e
−x
2
.
Find derivatives of sinh x and cosh x and express your answers in terms of sinh x and cosh x.
Use those formulas to find derivatives of y = x sinh x and y = cosh(x
2
).
Solutions:
1. (a) Using product rule with f(x) = x
2
+ 1 and g(x) = e
3x
and chain for derivative of g(x)
obtain y
0
= 2xe
3x
+ 3e
3x
(x
2
+ 1).
(b) Use the chain rule. y
0
= e
x
2
+3x
(2x + 3)
(c) The quotient rule with f(x) = e
2x
+ e
−2x
and g(x) = x
2
and the chain for f
0
(x) = 2e
2x
−
2e
−2x
produces y
0
=
(2e
2x
−2e
−2x
)x
2
−2x(e
2x
+e
−2x
)
x
4
=
2x((x−1)e
2x
−(x+1)e
−2x
)
x
4
=
2((x−1)e
2x
−(x+1)e
−2x
)
x
3
.
(d) Use the chain rule. y
0
= 3
x
2
+3x
ln 3(2x + 3)
(e) Use the product rule with f(x) = x and g(x) = 5
3x
and the chain for g
0
(x) = 5
3x
ln 3(3)
so that y
0
= 5
3x
+ 3x ln 5 5
3x
.
(f) y =
1
2
(3
x
−3
−x
). The derivative of 3
x
is 3
x
ln 3 and, using the chain rule with inner function
−x, the derivative of 3
−x
is 3
−x
ln 3(−1) = −3
−x
ln 3. Thus y
0
=
1
2
(3
x
ln 3 + 3
−x
ln 3) =
ln 3
2
(3
x
+ 3
−x
).
(g) Use the product rule with f = x and g = e
ax
2
+1
. Use the chain rule to find the derivative
g
0
as e
ax
2
+1
a 2x. Thus y
0
= e
ax
2
+1
+ 2ax
2
e
ax
2
+1
.
(h) Use the chain rule. y
0
=
ae
x
2
√
1+ae
x
.
(i) The chain rule with inner 2x + e
x
2
and another chain rule for derivative of e
x
2
produces
y
0
= 4(2x + e
x
2
)
3
· (2 + e
x
2
2x) = 8(1 + xe
x
2
)(2x + e
x
2
)
3
.
(j) Chain rule: y
0
=
1
x
2
+2x
(2x + 2) =
2x+2
x
2
+2x
(k) Chain rule: y
0
=
3
ln 2(3x+4)
(l) Chain and product y
0
= ln(x
2
+ 1) +
2x
2
x
2
+1
(m) Chain rule: y
0
=
2x
ln 3(x
2
+5)
(n) Product and quotient: y
0
=
(ln x+1)(x
2
+1)−2x
2
ln x
(x
2
+1)
2
(o) Chain rule twice: y
0
=
1
x+5e
3x
(1 + 5e
3x
3) =
1+15e
3x
x+5e
3x
(p) Product and chain: y
0
= a ln(x
2
+ b
2
) +
2x
x
2
+b
2
ax = a ln(x
2
+ b
2
) +
2ax
2
x
2
+b
2
.
(q) Use logarithmic differentiation ln y = ln(3x)
5x
= 5x ln(3x) ⇒
1
y
y
0
= 5 ln(3x) +
3
3x
5x ⇒
y
0
= (5 ln(3x) + 5)y ⇒ y
0
= (5 ln(3x) + 5)(3x)
5x
.

(r) Use logarithmic differentiation y = x
ln x
⇒ ln y = ln x
ln x
= ln x ln x = (ln x)
2
⇒
1
y
y
0
=
2 ln x
1
x
⇒ y
0
= (2 ln x
1
x
)x
ln x
.
(s) Use logarithmic differentiation ln y = ln(ln x)
x
= x ln(ln x) ⇒
1
y
y
0
= ln(ln x) +
1
ln x
1
x
x ⇒
y
0
=
ln(ln x) +
1
ln x
y ⇒ y
0
= (ln(ln x) +
1
ln x
)(ln x)
x
.
(t) Use logarithmic differentiation ln y = ln(3x+2)
2x−1
= (2x−1) ln(3x+1) ⇒
1
y
y
0
= 2 ln(3x+
1) +
3(2x−1)
3x+2
⇒ y
0
=
2 ln(3x + 1) +
3(2x−1)
3x+2
y ⇒ y
0
= (2 ln(3x + 2) +
3(2x−1)
3x+2
)(3x + 2)
2x−1
.
2. (a) Take log
2
of both sides. Get x −1 = log
2
(5) ⇒ x = log
2
(5) + 1 = 3.32. Alternatively, take
ln of both sides and get (x − 1) ln 2 = ln 5 ⇒ x =
ln 5
ln 2
+ 1 = 3.32.
(b) Take log
3
of both sides, get 2x + 3 = log
3
(7). Solve for x and get x =
log
3
(7)−3
2
= −.61.
(c) Take ln of both sides. Get 3x + 4 = ln 2 ⇒ x =
ln 2−4
3
= −1.1.
(d) (3.2)
x
= 64.6 ⇒ x ln 3.2 = ln 64.6 ⇒ x =
ln 64.6
ln 3.2
= 3.58.
(e) log
3
(x + 4) = 1 ⇒ 3
log
3
(x+4)
= 3
1
⇒ x + 4 = 3 ⇒ x = −1.
(f) log
5
(x
2
+ 9) = 2 ⇒ 5
log
5
(x
2
+9)
= 5
2
⇒ x
2
+ 9 = 25 ⇒ x
2
= 16 ⇒ x = ±4.
(g) ln(ln x) = 0 ⇒ ln x = e
0
⇒ ln x = 1 ⇒ x = e
1
= e ≈ 2.72
(h) Note that ln e
3
simplifies as 3. Thus ln(x + 2) + 3 = 7 ⇒ ln(x + 2) = 4 ⇒ x + 2 = e
4
⇒
x = e
4
− 2 = 52.6.
3. The derivative of sinh x =
1
2
(e
x
− e
−x
) is
1
2
(e
x
− e
−x
(−1)) =
1
2
(e
x
+ e
−x
) = cosh x. Similarly,
obtain that the derivative of cosh x is sinh x. Using the product rule obtain that the derivative
of y = x sinh x is y
0
= sinh x + x cosh x. Using the chain rule obtain that the derivative of
y = cosh(x
2
) is y
0
= sinh(x
2
)(2x) = 2x sinh x.
