NBER WORKING PAPER SERIES
DEMOGRAPHICS AND FDI:
LESSONS FROM CHINA'S ONE-CHILD POLICY
John B. Donaldson
Christos Koulovatianos
Jian Li
Rajnish Mehra
Working Paper 24256
http://www.nber.org/papers/w24256
NATIONAL BUREAU OF ECONOMIC RESEARCH
1050 Massachusetts Avenue
Cambridge, MA 02138
January 2018
We thank Julien Penasse, Ed Prescott, and Laszlo Sandor for helpful comments and suggestions.
Theviews expressed herein are those of the authors and do not necessarily reflect the views of the
NationalBureau of Economic Research.
NBER working papers are circulated for discussion and comment purposes. They have not been
peer-reviewed or been subject to the review by the NBER Board of Directors that accompanies
officialNBER publications.
© 2018 by John B. Donaldson, Christos Koulovatianos, Jian Li, and Rajnish Mehra. All rights
reserved. Short sections of text, not to exceed two paragraphs, may be quoted without explicit
permission providedthat full credit, including © notice, is given to the source.

Demographics and FDI: Lessons from China's One-Child Policy
John B. Donaldson, Christos Koulovatianos, Jian Li, and Rajnish Mehra
NBER Working Paper No. 24256
January 2018
JEL No. E13,F11,F12,J11,O11
ABSTRACT
Lucas (1990) argues that the neoclassical adjustment process fails to explain the relative paucity
ofFDI inflows from rich to poor countries. In this paper we consider a natural experiment: using
Chinaas the treated country and India as the control, we show that the dynamics of the relative
FDI flowssubsequent to the implementation of China's one-child policy, as seen in the data, are
consistent with neoclassical fundamentals. In particular, following the introduction of the one-
child policy in China, the capital-labor (K/L) ratio of China increased relative to that of India,
and, simultaneously, relative FDI inflows into China vs. India declined. These observations are
explained in the context of a simple neoclassical OLG paradigm. The adjustment mechanism
works as follows: the reduction in the (urban)labor force due to the one-child policy increases the
savings per capita. This increases the K/L ratio and reduces the marginal product of capital
(MPK). The reduction in MPK (relative to India) reducesthe relative attractiveness of investment
in China and is thus associated with lower FDI/GDP ratios.Our paper contributes to the nascent
literature exploring demographic transitions and their effects onFDI flows.
John B. Donaldson
Columbia Business School
3022 Broadway, Uris Hall
New York, NY 10027-6902
Christos Koulovatianos
Department of Economics
University of Luxembourg
162A avenue de la Faïencerie
/Luxembourg
Jian Li
'HSDUWPHQWRI(FRQRPLFV
8QLYHUVLW\RI/X[HPERXUJ
$DYHQXHGHOD)DwHQFHULH
//X[HPERXUJ
Rajnish Mehra
Department of Economics
W. P. Carey School of Business
Arizona State University
PO Box 879801
Tempe, AZ 85287-9801
and NBER

1. Introduction
In an inuential paper Lucas (1990) argued that the neoclassical adjustment process (capital
owing to its highest rate of return use) fails to explain the relative paucity of foreign direct
investment (FDI) inows to poor countries from rich ones, compared to ows among rich
countries themselves.
1
In this context the expressions rich and poor refer to countries
with high and low capital-labor (K/L) ratios, with the latter generating higher capital re-
turns. A country may be poor in terms of GDP per capita yet relatively rich in terms
of its K/L ratio. For the neoclassical adjustment process it is the latter identication that
matters.
In this paper we revisit the Lucas (1990) paradox in the context of a natural experiment:
the imposition, in 1982, of Chinas mandatory one-child policy. Keeping India, (where an
incentivized but voluntary two-child policy was largely ine¤ective) as the control, we compare
macroeconomic data from the two countries and nd that post 1982 the FDI/GDP ratio has
been increasing in both countries but declining in China relative to India. We show these
observations to be consistent with a neoclassical adjustment process by replicating them in a
two-country (and rest of the world) overlapping generations (OLG) model with neoclassical
fundamentals.
A key feature of the analysis is di¤erential population (labor-force) growth rates and, in
particular, a sudden, exogenous decline in the growth rate in one of the countries. This results
in the national savings of the older generation accruing to a smaller younger generation. The
resulting higher capital-labor ratio in turn leads to lower capital returns, discouraging FDI
investment. If capital adjustment costs are present, the same phenomena are observed for
a prolonged time. Consistent with the models implications, we see that the trajectory of
1
Alfaro et al. (2008, Figure 1, p. 352) support the Lucas (1990) paradox, using data from 23 developed
and 75 developing countries.
1

the capital growth di¤erences between India and China closely tracks the di¤erence in their
respective population growth rates.
2
Di¤erences in the evolution of the K/L and FDI/GDP ratios in China vs. India may
have non-demographic origins. Within the context of the model we consider, di¤erences in
the labor productivity growth rate could have similar e¤ects. We net out this possibility
by computing labor productivity growth in China and India for the periods preceding and
following the 1982 one-child policy intervention.
3
We nd the productivity di¤erences to have
been very small, allowing us to focus on the e¤ects caused by the exogenous intervention on
the population growth rate of China.
4
The broad message of the paper is two fold. First, relative population dynamics play
a rst order role in determining cross country FDI ows.
5
Second, accounting for these
dynamics suggests that the post 1982 macroeconomic observations from India and China
are consistent with neoclassical theory.
6
2
Our models mechanism requires that saving rates do not drop more than the rate at which savings per
young worker increase. Choukhmane et al. (2007) document a sharp rise in the Chinese saving rate after
the policy had been implemented, giving empirical support to the models mechanism.
3
Rosenzweig and Zhang (2009) nd a modest impact of the one-child policy on human capital (in the
child-quality sense). This nding supports that the one-child policy has not led to other neglected factor-
accumulation e¤ects that may bias our results on the dynamics of physical-capital accumulation in this
paper.
4
The similarities in productivity di¤erences between China and India are also supported by Hsieh and
Klenow (2009), and Bollard, Klenow and Sharma (2013).
5
A cogent reason to focus on determinants of FDI, such as population dynamics, is that for many countries
FDI is one of the ways out of poverty traps: see, for example, deMello (1997, Table 3), for an early survey of
the positive relationship between FDI and growth (including some Granger causality tests), and also Basu
and Guariglia (2007) for further evidence from 119 countries, conrming this positive channel. For an essay
on poverty traps and FDI see Azariadis (1996, pp. 464-5).
6
Specically, our analysis suggests that that the dynamic FDI paradigm employed in McGrattan and
Prescott (2009, 2010) and Holmes, McGrattan and Prescott (2015) may fruitfully be extended to accom-
modate di¤erent cross-country population growth rates. The support we nd in favor of neoclassical the-
ory contributes to the unresolved debate on ideas vs factor accumulation (see, for example, Klenow and
Rodriguez-Clare, 1997, and Klenow, 1998). According to this debate, it is di¢cult to decide which venue to
use for models of development: neoclassical production functions, or models of innovation, expanding variety
of intermediate and nal goods, or technology adoption? A notable study explaining why this comparison
is di¢cult is Hall and Jones (1999, Table 1, p. 91).
2

2. The Model
We construct a parsimonious OLG model of two countries, 1 and 2, and the rest of the world
(ROW). We assume that countries 1 and 2 are price takers in international capital markets,
where the world interest rate, denoted by r
, is constant. For simplicity, we focus on FDI
from ROW to these two countries. Our key simplifying assumptions are:
- Capital ows from ROW to countries 1 and 2, but there are no capital ows
between countries 1 and 2.
- The labor force of each country cannot move to other countries.
- There is no international trade in nal goods.
7
None of these assumptions compromise the generality of our main results.
2.1 Production
Aggregate domestic production in country i 2 f1; 2g in period t is characterized by the
production technology,
Y
i;t
= Y
i
i;t
+ Y
r
i;t
, (1)
where,
Y
i
i;t
=
K
i
i;t
i
A
i
i;t
L
i
i;t
1
i
,
i
2 (0; 1) (2)
and
Y
r
i;t
=
F DI
r
i;t
i
A
r
i;t
L
r
i;t
1
i
. (3)
7
This is a simplifying assumption, following Backus, Kehoe, and Kydland (1992) and Holmes, McGrattan
and Prescott (2015). While there are plausible reasons to assume that FDI may be more focused on selling
in a local market rather than as a base for exports (see the discussion in Holmes, McGrattan and Prescott,
2015, p. 1159), this assumption is not critical for the qualitative conclusions implied by the model. Assuming
a fully integrated nal-goods market would add more arbitrage conditions but would not eliminate the key
arbitrage conditions behind the K/L ratio dynamics studied here. Our empirical application focuses on
China and India, two countries that have, historically, faced both geographical and political barriers to
capital ows and trade.
3

Subscripts denote the location of productive activity and superscripts denote the investing
country. Accordingly, K
i
i;t
is the period t capital of country i invested by domestic rms,
while F DI
r
i;t
is the stock of FDI capital invested by ROW rms in country i. L
i
i;t
is the
part of the workforce of country i working in rms using capital nanced by country i, while
L
r
i;t
denotes workers of country i that work for ROW companies using FDI. The common
depreciation rate for capital K
i
i;t
and F DI
r
i;t
is 2 (0; 1], for i 2 f1; 2g. The exogenous labor
productivity levels in the two sectors are denoted by A
i
i;t
and A
r
i;t
. The symbol A
r
i;t
allows
us to consider that productivity may be either location-specic or rm-specic. Factors
such as the extent of bureaucracy, infrastructure, political instability, etc., may cause the
productivity of a foreign rm to be location-specic. Furthermore, technology transfer (as,
e.g., in Holmes, McGrattan and Prescott, 2015), which we do not explicitly model, could
cause productivity to be rm-specic. In each country i, we postulate a large number of
identical rms operating the technologies described by equations (2) and (3).
Based on our assumption of no cross country labor force mobility, and assuming full
employment in each country,
L
i;t
= L
i
i;t
+ L
r
i;t
, (4)
where L
i;t
is the total workforce (population) in country i 2 f1; 2g. We assume that popu-
lation growth is exogenously given by,
L
i;t+1
L
i;t
= e
g
L;i;t+1
, t = 0; 1; ::: . (5)
Our production structure is a simplied version of the one in McGrattan and Prescott
(2009, 2010) and Holmes et al. (2015), with some modications to the role of labor in
production.
8
8
The McGrattan and Prescott (2009, 2010) models assume that total population, L
i;t
, enters the produc-
tion function of both companies relying on domestic capital and of companies relying on FDI. Using the
4

2.2 E¢cient factor allocation
The representative rm, i or r, located in country i 2 f1; 2g, is prot maximizing in an en-
vironment of perfectly-competitive factor markets. Accordingly, factor demands are driven
by equating marginal products to factor prices. In addition, since rm production functions
exhibit constant returns to scale and factor ows within a country are frictionless, the com-
petitive equilibrium e¢ciently allocates factor inputs
K
i
i;t
; F DI
r
i;t
; L
i
i;t
; L
r
i;t
in each country
to maximizing domestic production (see also McGrattan and Prescott, 2009, 2010).
The intra-temporal conditions for the e¢cient allocation of factor inputs,
K
i
i;t
; F DI
r
i;t
; L
i
i;t
; L
r
i;t
,
in order to maximize Y
i;t
, subject to,
K
i;t
= K
i
i;t
+ F DI
r
i;t
, and L
i;t
= L
i
i;t
+ L
r
i;t
, (6)
where K
i;t
is total country i capital and L
i;t
total country i labor, are,
MP K
i
i;t
= MP K
r
i;t
, (7)
and,
MP L
i
i;t
= MP L
r
i;t
. (8)
Here MPK and MPL signify the marginal product of capital and marginal product of
labor respectively.
abstractions and notation of our model, domestic production in a McGrattan and Prescott (2009, 2010) type
of model would be,
Y
i;t
=
K
i
i;t
i
A
i
i;t
1
i
+
K
j
i;t
i
A
j
i;t
1
i
(L
i;t
)
1
i
:
They motivate their formulation by the observed correlation between population size and FDI-location ca-
pacity. The McGrattan and Prescott (2009, 2010) formulation is convenient for obtaining an aggregate
Cobb-Douglas domestic-production function. In this paper we suggest company-specic Cobb-Douglas pro-
duction technologies and clearly distinguish those who work in FDI-related companies and those who work
in domestically nanced companies.
5
2.3 Households, domestic savings, and national capital
We use a variant of the overlapping-generations (OLG) model developed in Diamond (1965).
Individuals live for two periods. Omitting subscript i, unless necessary, the following notation
applies:
c
1;t
consumption of a young agent born at time t (t species the generation)
c
2;t
consumption when old at time t + 1 of an individual born at time t
L
t
number of individuals born in period t and working in period t
w
t
wage received in period t
r
t+1
interest rate paid on savings held from period t to period t + 1.
This notation implies that aggregate consumption in period t + 1 is L
t
c
2;t
+ L
t+1
c
1;t+1
(See Table 1 below)
Table 1 The evolution of consumption.
Periods
t
t + 1 t + 2 t + 3
Age born in t c
1;t
c
2;t
Groups born in t + 1 c
1;t+1
c
2;t+1
born in t + 2 c
1;t+2
c
2;t+2
aggregating L
t
c
2;t
+ L
t+1
c
2;t+1
+
L
t+1
c
1;t+1
L
t+2
c
1;t+2
We further assume:
6

1. Within each cohort, individuals are identical. The utility function of a repre-
sentative individual is given by,
U (c
1;t
; c
2;t
) = log (c
1;t
) + log (c
2;t
) , with discount factor 2 (0; 1) . (9)
2. Labor supply is completely inelastic and equal to one unit per period. Ac-
cordingly, the labor income of an individual when working in period t is w
t
.
3. When young, individuals work, consume and accumulate capital (save). When
old, individuals rent their capital to rms (in which the young generation works),
consume, and die.
The consumption of generation t, when old (occurring in period t + 1), is thus given by,
c
2;t
= (1 + r
t+1
) s
t
, (10)
where s
t
denotes period t savings of a household. Since the only source of income when
young is the wage income w
t
, s
t
= w
t
c
1;t
, and (10) becomes,
c
1;t
+
c
2;t
1 + r
t+1
= w
t
. (11)
Maximizing lifetime utility (9) subject to the lifetime constraint (11) yields,
s
t
=
1 +
w
t
. (12)
Aggregate domestic savings of the young generation, S
i;t
= s
i;t
L
i;t
, is equal to aggregate
investment, which augments the national capital stock of the country in period t. Equation
(12) then implies,
K
i
i;t
= (1 ) K
i
i;t1
+
i
1 +
i
w
i;t1
L
i;t1
| {z }
q
S
i;t1
, i 2 f1; 2g . (13)
7

In Appendix A we show that under one additional assumption,
A
i
i;t
= A
r
i;t
= A
i;t
, t = 0; 1; :::, (14)
production in both countries i 2 f1; 2g is given by an aggregated domestic production
function of the form,
Y
i;t
= K
i
i;t
(A
i;t
L
i;t
)
1
i
=
K
i
i;t
+ F DI
r
i;t
i
(A
i;t
L
i;t
)
1
i
. (15)
This special case allows the derivation of analytical results with direct empirical impli-
cations. Nevertheless, assuming A
i
i;t
6= A
j
i;t
, and A
j
j;t
6= A
i
j;t
, qualitatively gives the same
empirical implications as described below, while depriving us of certain useful formulae that
follow later in the paper. In what follows, we thus maintain assumption (14).
9
2.4 Capital adjustment costs
In the absence of any capital adjustment cost, optimal investment is governed by,
r
+ = MP K
i;t
, i 2 f1; 2g . (16)
With frictionless capital ows and unlimited capital availability at the world cost of capital
r
, steady state transitions due to underlying parameter changes will occur in one period
which, in this model, corresponds to one-half of an adult lifetime. In order to better match
the empirical duration of transitions we impose a capital adjustment cost on the dynamics
implied by equations (13) and (16). In particular, we modify equation (16) to be of the form:
r
+ = MP K
i;t
+ (t;
t) , i 2 f1; 2g , (17)
where,
(t;
t) =
8
>
<
>
:
0
(1 )
t
t1
,
,
if t
t
if
t + 1 t
, (18)
9
We also assume that A
i
i;t
= A
r
i;t
because we lack any data on labor productivity growth in foreign owned
vs. domestically owned rms.
8

where > 0, 2 ( 0; 1). The symbol
t > 0 denotes the period in which an exogenous
intervention shocks equilibrium away from its steady-state path. For some periods after a
transitional shock there is a loss of (1 )
t
t1
in capital returns, which we postulate as due
either to costs of industrial relocation, or to institutional adjustments such as bureaucratic
or political frictions.
10
These institutional adjustments are gradually smoothed out, and the
capital-returns wedge, , decays over time at rate .
2.5 Equilibrium
Equilibrium is characterized by a set of prices and quantities at which all rms maximize
prots, all households maximize utility as price takers given these equilibrium prices and all
domestic and international markets clear at these equilibrium prices and quantities.
In the model with adjustment costs, equilibrium in country i 2 f1; 2 g is characterized by
conditions (13) and (17), with adjustment costs introducing long-lasting transitions in the
capital labor ratio. In a steady state, adjustment costs are zero by construction.
In the next sections we study the e¤ects of an exogenous demographic intervention on the
K/L ratio and FDI. The intervention is characterized by a sudden decrease in population
growth in one of the two countries, similar to the introduction of the one-child policy in
China. This intervention puts a country in a transition characterized by changes in its K/L
ratio and FDI ows. Specically, following a drop in population growth, momentum in
capital dynamics, exaggerated by capital-adjustment costs, increases the K/L ratio, which
leads to a drop in the marginal product of capital, that, in turn, discourages FDI ows.
10
The exogenous wedge that we impose upon condition (16) through equations (17) and (18) is similar to
measured wedges that reect deviations from the covered interest rate parity condition observed by Du,
Tepper, and Verdelhan (2017) after the recent nancial crisis. Du, Tepper, and Verdelhan (2017) attribute
these deviations to costs through bank regulation. They can be seen as adjustment costs of moving from
pre-crisis to post-crisis leverage ratios. For some countries, these covered interest rate parity deviations were
stronger during the nancial crisis crisis and then started fading away over time, as equation (18) implies
(Du, Tepper, and Verdelhan, 2017, Figure 2).
9

To analyze these e¤ects fully, we rely on specic relationships describing K/L ratio dy-
namics both along the transition path toward the steady-state growth path, and along the
steady state growth path itself. These are presented below:
a) Transition Dynamics
Equation (17) implies,
K
i;t
A
i;t
L
i;t
=
i
r
+ (t;
t)
1
1
i
. (19)
In turn, equation (19) implies that the growth rates of capital, labor and labor productivity
are jointly related according to
g
K;i;t
ln (K
i;t
) ln (K
i;t1
) =
1
1
i
ln
r
+ (t 1;
t)
r
+ (t;
t)
+ g
A;i;t
+ g
L;i;t
. (20)
From equation (20) we see that an exogenous demographic intervention that reduces popu-
lation growth from a constant rate g
L;i
to a lower constant rate g
L;i
, will also cause a drop in
the growth rate of domestic capital, absent any other changes in labor productivity growth.
b) Steady State Growth Dynamics ( (t;
t) = 0)
We maintain our assumption that population growth is constant and further assume that
productivity growth is also constant over time in country i 2 f1; 2g, i.e.,
L
i;t+1
L
i;t
= e
g
L;i
,
A
i;t+1
A
i;t
= e
g
A;i
. (21)
In conjunction with (17) and (18), equation (15) yields,
r
+ =
@Y
i;t
@K
i;t
MP K
i;t
= MP K
i
i;t
= MP K
r
i;t
, i 2 f1; 2g . (22)
In Appendix B we show that the steady state growth path in economy i is characterized
by equations,
Y
ss
i;t
L
i;t
=
i
r
+
i
1
i
A
i;t
, (23)
10

K
i
i;t
ss
L
i;t
=
i
(1
i
)
(1 +
i
) (e
g
A;i
+g
L;i
+ 1)
i
r
+
i
1
i
A
i;t
, (24)
and,
F DI
r
i;t
ss
Y
ss
i;t
=
i
r
+
i
(1
i
)
(1 +
i
) (e
g
A;i
+g
L;i
+ 1)
. (25)
Equation (24) implies that an exogenous demographic intervention that reduces population
growth from a constant rate g
L;i
to another lower constant rate g
L;i
, will permanently increase
national capital per worker. This permanent increase in
K
i
i;t
ss
=L
i;t
reduces capital returns.
By equation (25), the crowding out of FDI will also cause a drop in the long run steady-state
level of the FDI/GDP ratio.
11
Equations (19) - (25), all of which are neoclassical in origin,
form the backbone of the analysis to follow.
In the next section we rst detail the empirical behavior of K, L, and K=L in China and
India before and after Chinas one-child policy implementation, and then demonstrate that
a reasonably parameterized version of the present model replicates this behavior.
2.6 Comparative population policies in China and India
The two countries with the largest populations in the world, China and India, o¤er a unique
contrast regarding population policy. Both countries initiated public policies to control
population growth. In India a two-child birth regulation policy was voluntary and ine¤ective.
In contrast, Chinas one-child policy was mandatory and e¤ective.
11
The expression crowding out implies that the lower capital returns which follow on higher K/L ratios
reduce the incentives for foreign rms to undertake FDI.
11
0
250
500
750
1000
1250
1500
Population (million)
1950
1975
2000
2015
2030
2050
2075
2100
observed median-prediction
95% pred. interval 80% pred. interval
Source: United Nations, Depart ment of Economic and Social Affairs
Population Division (2015)
China: Population (Age 15-59)
0
250
500
750
1000
1250
1500
Population (million)
1950
1975
2000
2015
2030
2050
2075
2100
observed median-prediction
95% pred. interval 80% pred. interval
Source: United Nations, Depart ment of Economic and Social Affairs
Population Division (2015)
India: Population (Age 15-59)
Figure 1 Population dynamics in China and India. The two green lines indicate that,
until 2030, predictions of working population dynamics are robust to any
population-growth scenario.
Figure 1 demonstrates the scope of this major exogenous demographic policy intervention,
which qualies as a natural experiment. It depicts actual and predicted population dynamics
according to various population growth scenarios and condence intervals obtained through
a Bayesian averaging method. Both data and population projection scenarios in Figure 1
are obtained from the United Nations Population division. Computations are done using an
open source package described in Raftery et al. (2012) and Gerland et al. (2014). Three
key observations result:
12

1. In China, an absolute decline in the working population (aged 15-59) began
in 2010 and is predicted to continue under all reasonable scenarios.
2. In India the working population is predicted to continue growing at least until
2030.
3. After 2025, the working-aged population in India will exceed that of China.
These three points show that Chinas policy intervention was not only e¤ective almost
immediately after implementation but also that its e¤ects on population dynamics are ex-
pected to persist beyond one generation.
12
The anticipation of these persistent policy e¤ects
is crucial for investment decisions because investors are forward-looking and major invest-
ments are typically long-lived. The combination of contemporaneous and expected future
e¤ects of the one-child policy on these comparative population dynamics strengthens the
impact of the natural experiment. Furthermore, we show in Table 2 that crucial growth-
performance features, such as productivity growth and GDP growth, were similar in China
and India before and, most especially, after the exogenous demographic intervention. This
similarity allows us to plausibly attribute trend di¤erences between China and India solely
to the exogenous demographic intervention in China.
As shown in Table 2, both China and India experienced very similar rapid GDP growth
in the period after the implementation of the one-child policy in China. (see the two columns
under g
Y
in Table 2). Based on the production function given in (15), the two columns
under g
A
, labor productivity growth, have been calculated using the corresponding formula
g
A
= (g
Y
g
K
) = (1 ) g
L
(we have assumed that the capital intensity parameter,
= 1=3 in both China and India). Note that productivity growth, g
A
was also similar in
12
The recently introduced two-children policy in China is likely to alter the anticipated population dynamics
in China, depicted in the left panel of Figure 1, after 2030. Nevertheless, predictions about population
dynamics 15 years ahead will not be a¤ected. These predictions are captured later in the time interval
bracketed by the vertical dashed lines.
13

China and India both in Period 1, and even more so in Period 2 while increasing in both.
The capital stock grew more rapidly in China in the latter period, while the dramatic labor
force growth slowdown in China is clearly evident in the g
L
column.
Table 2 Growth rates of macro aggregates. Annual rates (%).
(i) (ii) (iii) (iv)
g
L
g
K
g
Y
g
A
China India China India China India China India
Period 1 (1960-1981)
2:05 2:27 7:89 3:52 5:11 4:14 1:69 2:17
Period 2 (1982-2014) 0:82 1:99 13:97 12:42 9:14 9:28 5:94 5:74
Source: Penn World Tables and United Nations.
g
L
- growth rate of labor
g
K
- growth rate of capital
g
Y
- growth rate of GDP
g
A
- growth rate of labor productivity
Let g
x;t
g
x;1;t
g
x;2;t
, with country 1 being China and country 2 being India. Figure
2 plots the empirical g
L;t
(red line) and g
K;t
(blue line), and identies the date when
the one-child policy was implemented (1982). Solid lines are the Hodrick-Prescott ltered
series. Only a few years after 1982, g
L;t
takes on negative values and decreases over time
(right axis in Figure 2), demonstrating that there has been a strong exogenous demographic
intervention in China relative to India.
14
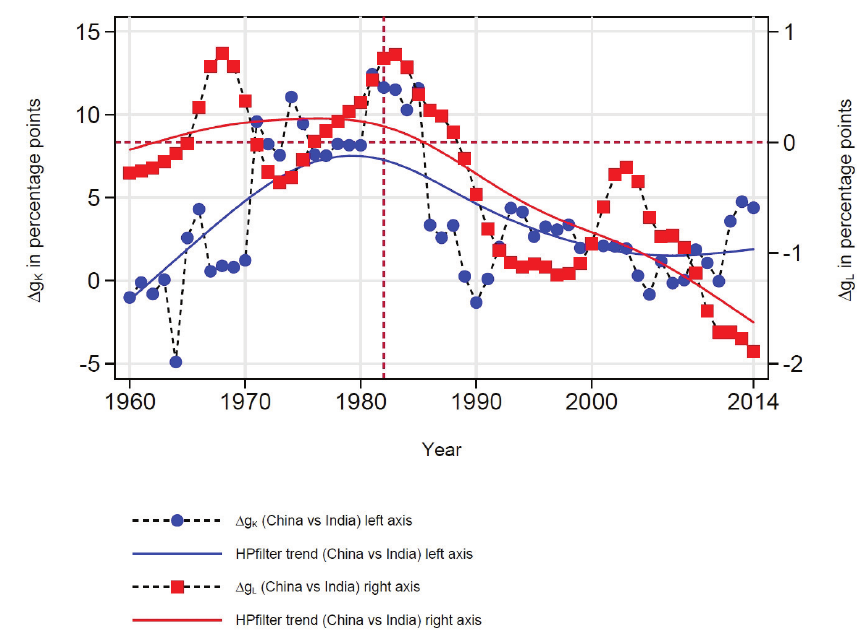
A key feature of Figure 2 is the simultaneity in the reversal of the trajectory of g
L;t
and
the reversal of the trajectory of g
K;t
after 1982. It supports our hypothesis that Chinas
exogenous demographic intervention has played a crucial role in explaining the di¤erential
capital-accumulation dynamics in the two countries after 1982.
That g
K;t
is positive after 1982 is not a surprise, as g
A
rose from 0:48% before 1982
to 0:20% after 1982 (see Table 2). This rise in g
A
is not, however, strong enough to mask
the impact of population growth on capital growth.
Figure 2 - Di¤erential growth rates of capital and labor: China vs India.
To demonstrate the mechanics of our model we provide a numerical example of a country
where an exogenous demographic intervention occurs in period 10. All model parameter
15

values are given by Table 3.
13
The drop in population growth rate due to the intervention is
similar to that of the one-child policy in China. The chosen value for is taken from Klenow
and Rodriguez-Clare (1997, p. 76), while the value of r
is in accordance with estimates in
Holston, Laubach, and Williams (2017).
Table 3 - Parameter values.
Parameters
T Length of period 25
(1-)/ Annual rate of time preference 6%
g
A
Annual labor productivity growth rate 4%
g
L
Annual population growth rate 2%
g
L
1
Annual population growth rate after intervention -1.0%
Output elasticity of capital 1/3
r
Annual world interest rate 3%
Annual depreciation rate 3%
Wedge on world capital return (annual)% 0.5%
Rate of decay of the world-interest rate wedge 30%
Since Indias demographic-control policies were broadly ine¤ective and it was exposed to
the same extant globalization factors as China (especially in the mid-1990s), we postulate
that India remained close to a steady-state path, and examine the di¤erence in the capital
growth rate between the two countries. In particular, equation (20) can be re-written as,
g
K;t
=
1
1
1
ln
r
+ (t 1;
t)
r
+ (t;
t)
+ g
L;t
+ g
A;t
, (26)
where g
x;t
g
x;1;t
g
x;2;t
, with country 1 being China and country 2 being India. Equa-
tion (26) governs the capital-labor (K/L) ratio dynamics depicted in Figure 3, and o¤ers
a rst model test regarding the one-child policy in China and its comparison with India.
If neoclassical K/L ratio mechanics are indeed present in China and India then the e¤ect
13
Both economies in our analysis share the common parameter values of Table 3 except for g
L
which, for
the treated country only (China), changes from g
L
to g
L
1
.
16
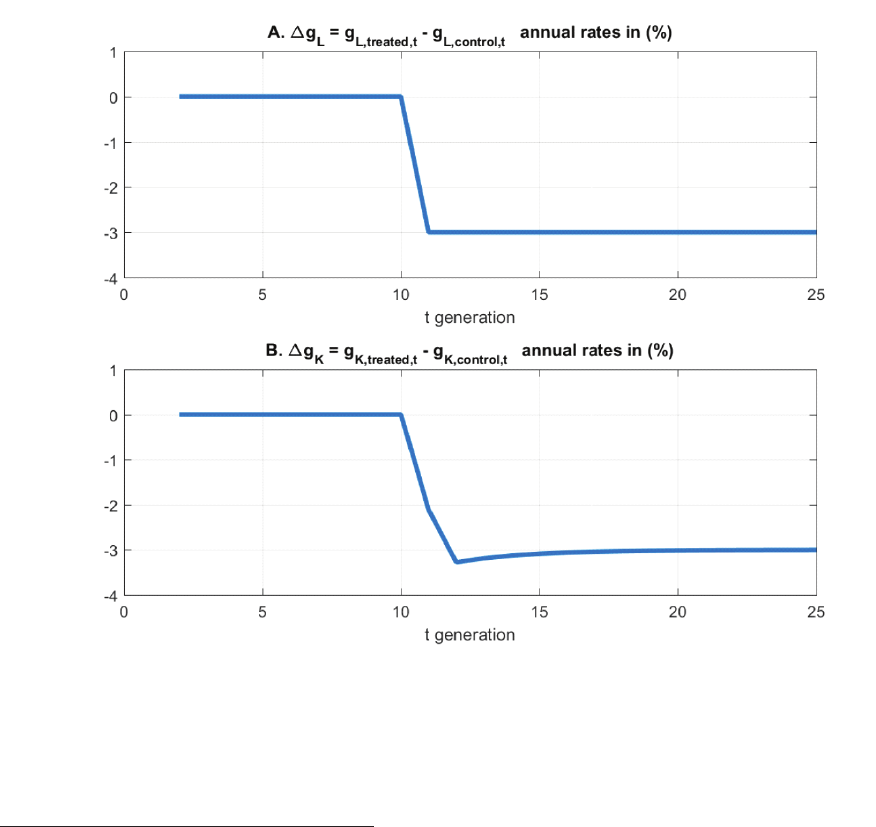
of the one-child policy in China is captured by an exogenous drop in g
L;t
, which, in turn
causes a drop in g
K;t
. In accordance with equation (26), if we observe that the dynamics
of g
K;t
track the dynamics of g
L;t
, then the neoclassical K/L ratio mechanics implied by
our parsimonious model are supported. Figure 3 presents the di¤erence between one country
experiencing an exogenous demographic intervention (the treated country), and a country
on its steady-state path (the control country).
14
Figure 3 The e¤ect of demographic intervention on the di¤erence in the capital growth
rate for the two economies parameterized as per Table 3, around the time of the
demographic intervention (treatment for one country only).
14
Note that the control country is initially identical to its treated counterpart even with regards to the level
of labor productivity.
17

Figure 3 shows that the natural experiment of the one-child policy is consistent with the
e¤ects predicted by a neoclassical model. Specically, Figure 2 lends empirical support to
the theoretical implications depicted in Figure 3.
3. The impact of an exogenous demographic intervention on rel-
ative FDI dynamics: theory and empirics
In this section we focus on FDI, specically the trajectories of capital inows from ROW.
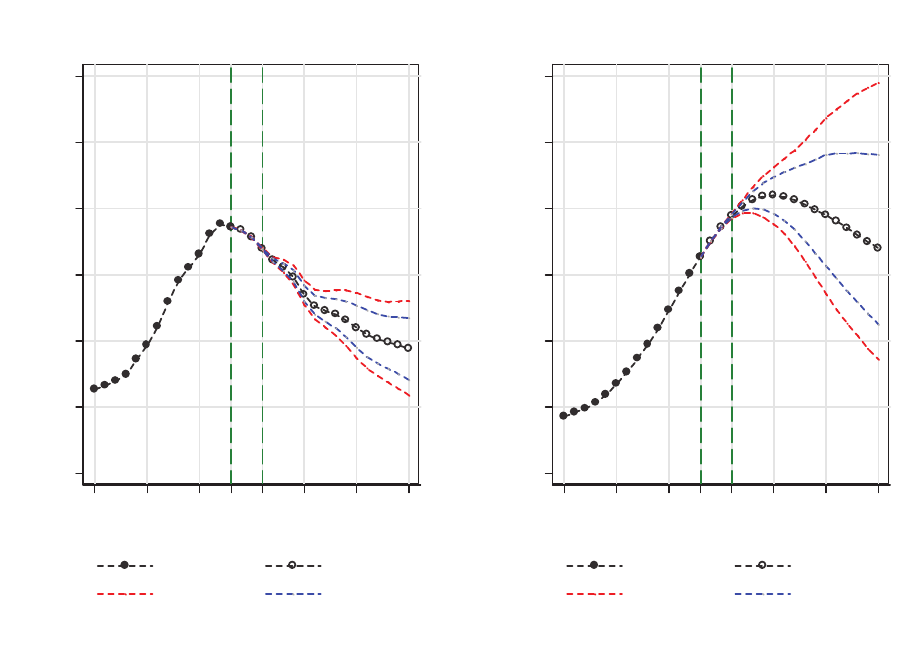
Using Table 3 parameter values, Figure 4 depicts model-generated di¤erences between one
country experiencing an exogenous period-10 demographic intervention (treated country),
and a country on its steady-state path (control country). Both countries are identical as
regards their initial K/L ratio and have identical labor productivity growth rates before
and after the intervention. Panels A, C and E describe the consequences for the treated
country alone while Panels B, D and F compare its response to the intervention with the
same quantity in the control country. To more fully assess the implications of Figure 4,
observe that if we consider two time series, x
t
and z
t
, and plot log (x
t
) log (z
t
) over time,
then an upward-sloping lo g (x
t
) log (z
t
) implies that x
t
grows faster than z
t
.
First consider Panels A and B of Figure 4. Following the demographic intervention,
the K/L ratio of the treated country spikes up (Panel A) before returning to its long run
steady state value.
15
As a result, the K/L ratio in the treated country increases relative to
the control country as captured in Panel B.
16
After some generations, the e¤ect disappears,
with the K/L ratio in both countries identical once again (Panel B). The K/L ratio e¤ects
are directly reected in the corresponding MPK values: the abrupt increase in the treated
15
As stressed above, in equation (19), capital in e¢ciency units, K= (AL), is tied to the world interest rate,
r
. In order to better understand the dynamics of K/L ratios we need to control for changes in the dynamics
of labor productivity, A, which we plot in Panel A of Figure 4 as K= (AL).
16
Following the identication mentioned in the preceding paragraph, the K/L ratio in the treated country
grew relative to its equivalent in the control country.
18
countrys K/L ratio has its counterpart in an absolute reduction in its MPK (Panel C), and
a relative MPK reduction vis-a-vis the control country (Panel D). Following equation (18),
adjustment costs of industrial relocation, and institutional adjustments such as bureaucratic
or political frictions are manifested through a temporary drop in capital returns, driven by
the capital-returns wedge (t;
t) = (1 )
t
t1
, that decays over time. Our choice of
parameter is an annual rate of 0:5%, and the decay parameter = 30% implies that the
half-life of this interest-rate wedge is about 50 years, which corresponds to two generations
of young workers, as the length of each period is 25 years. These values of and are
capable of reproducing empirically plausible K/L ratio dynamics.
Panels E and F detail the consequences of the intervention for the FDI/GDP ratio of the
treated country. As evident in equation (25), the steady state FDI/GDP ratio of country
i is positively related to its population growth rate g
L;i
. Accordingly, a reduction in the
treated countrys g
L;i
reduces its FDI/GDP ratio, an e¤ect manifested in Panel E. Relative
to the control country, its FDI/GDP ratio declines as well (Panel F). Although the K/L
ratio of the treated country eventually returns to its pre-intervention values (Panel A), the
composition of its ownership of its capital stock has changed in favor of proportionately
less FDI. We summarize these model implications as follows: a permanent decline in the
population growth rate of the treated country leads to, (i) a temporary (though prolonged)
increase (both absolute and comparative) in the K/L ratio above its steady state value,
and (ii) a permanent reduction in its FDI/GDP ratio both absolutely and relative to its
control counterpart. In summary, Figure 4 portrays the model implied consequences of a
sudden reduction in the treated countrys population growth rate on its K/L and FDI/GDP
dynamics: the K/L ratio grows and the FDI/GDP ratio declines, both absolutely and relative
to the control.
19
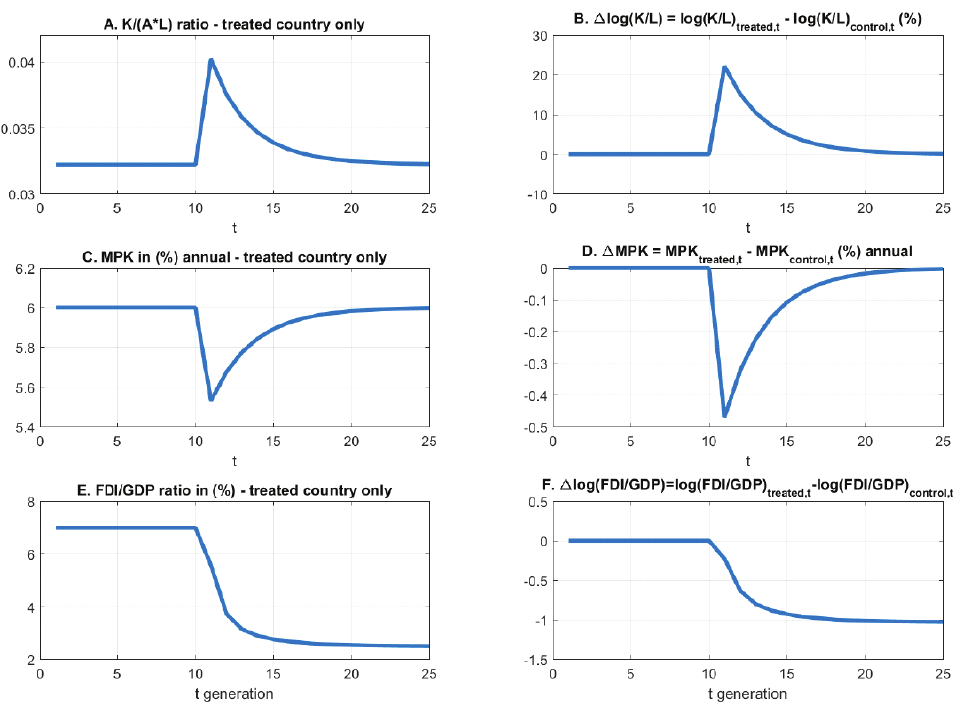
Figure 4 Comparative time paths of K/L, MPK and FDI/GDP, for the two economies
parameterized as per Table 3, around the time of the demographic intervention (treatment
for one country only).
We next examine the question of whether these e¤ects are in accordance with data. Figure
5 explores the empirical consistency of the one-child policy intervention in China.
20
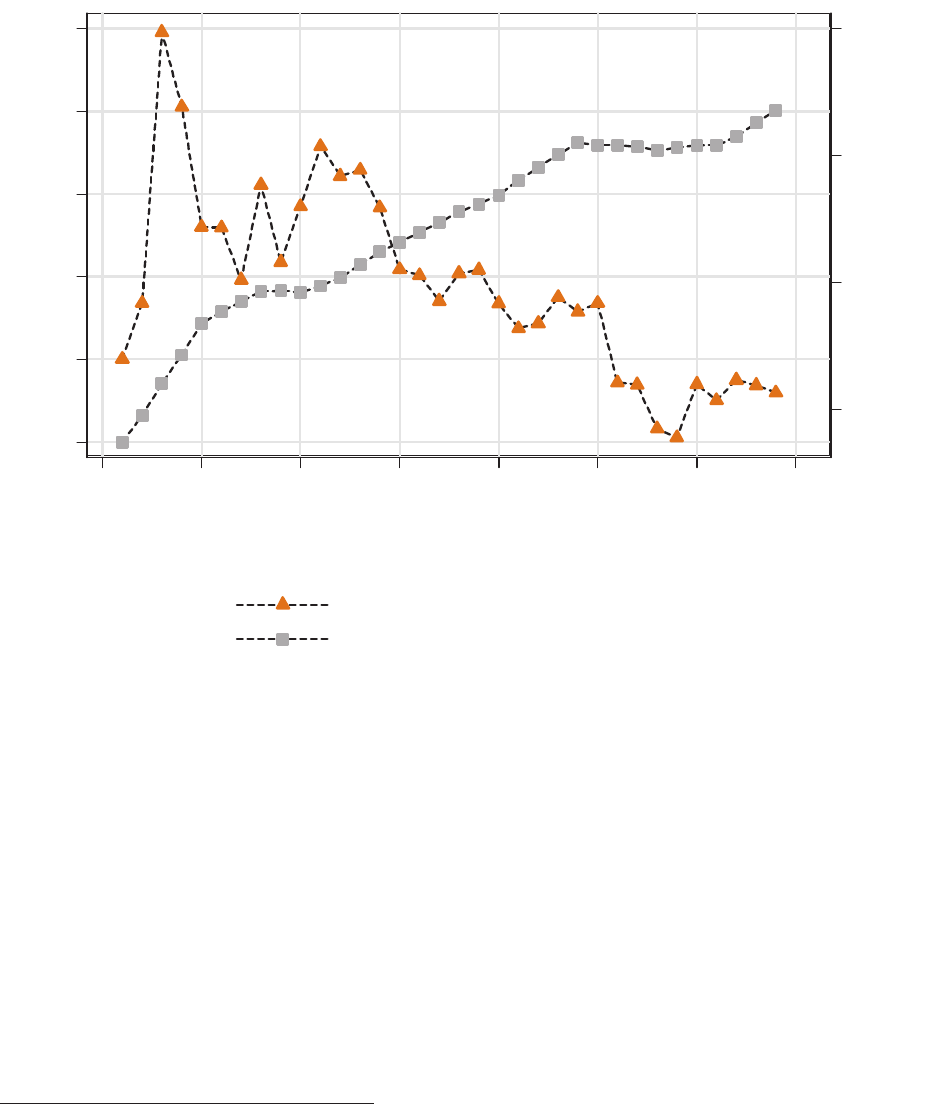
-.5
0
.5
1
K-L ratio
0
1
2
3
4
5
FDI intensity
1980 1985 1990 1995 2000 2005 2010 2015
year
log(FDI/GDP China) - log(FDI/GDP India), left axis
log(K-L ratio China) - log(K-L ratio India), right axis
Figure 5 - Di¤erential growth rates of FDI/GDP and K/L: China vs India.
In particular, post the 1982 demographic intervention, the K/L ratio of China grew more
rapidly than that of India. This empirical observation is in accordance with our models
implication in Panel B of Figure 4. During the same period, FDI intensity (measured by
FDI as a share of GDP) grew faster in India than in China. In 1990, the intensity of FDI
in China was about 30 times larger than that of India, but by 2014, the intensity of FDI
in China was less than 2 times that of India.
17
This empirical observation agrees with our
models implication as depicted in Panel E of Figure 4.
17
In Appendix C we document the data used in Figure 5 and o¤er a robustness check focusing on K/L
trends of the non-agricultural workforce in both countries (see Figure A.6 and Table A.1 in the Appendix).
It is important to note that FDI in China and India during the period examined did not represent the
purchase of existing domestic capital by foreign entities; rather observed FDI data predominantly describes
the formation of new capital.
21

The results depicted in Figure 5 do not contradict the Lucas paradox per se: FDI/GDP
and K/L were higher in China compared to India throughout the entire sample period.
18
It
suggests, however, that the search for neoclassical fundamentals underlying FDI ows may
be more productively undertaken by exploring cross-country relative rather than absolute
FDI dynamics.
19
4. Relationship to the existing literature
The neoclassical foundation for dynamic FDI analysis was rst articulated in McGrattan and
Prescott (2009, 2010), and Holmes, McGrattan and Prescott (2015). These three studies in-
troduce international capital ows in a fashion similar to the present model. The paradigms
they consider assume that both population growth rates and labor-productivity growth rates
are equal across countries (see McGrattan and Prescott, 2010, p. 1503, and Holmes, McGrat-
tan and Prescott, 2015, p. 1172), an assumption necessary for the existence of steady states
in their formulations.
20
In these papers both developed and developing countries have the
18
The present model is also able to replicate the Lucas (1990) paradox as a potential competitive equilibrium
outcome. To see this, rst note that by equation (24), the level of labor productivity, A
i
, inuences the
K/L ratio. By equation (25), however, the level of labor productivity has no inuence on the steady state
FDI/GDP ratio. Imagine two countries, one with a lower
i
, a higher level of capital intensity
i
, and
higher labor force and labor productivity growth rate. By equation (25) this country will have the higher
steady-state FDI/GDP ratio (r
and being common to both countries). If this country simultaneously
enjoys labor productivity A
i
dramatically above its counterpart, this high FDI/GDP ratio country will also
have a higher (K/L). Accordingly, more capital ows from the ROW to the richer of the two countries, where
we measure wealth in terms of capital per worker. This is one version of the Lucas (1990) paradox in our
neoclassical setting.
In fact, the high FDI/GDP, high A country described above resembles the USA in many respects: a
country with a high absolute TFP level, high TFP growth by developed world standards, a high income
share to capital and low savings (low ).
19
Notably, this natural experiment could not showcase these mechanics back in 1990, when the Lucas-paradox
paper was written.
20
To see why this paradigm does not allow for steady states with heterogeneous rates of population growth
across countries, consider an intertemporal Euler equation relating the growth rate of consumption to a
constant world interest rate, r
. With constant relative risk aversion , this Euler equation is given by
c
i
t+1
=c
i
t
= [ (1 + r
)]
1=
, with c
i
t
being consumption in country i. With ^c
i
t
denoting consumption in e¢ciency
units for a model with constant exogenous population growth rate, g
L;i
, and constant exogenous labor
productivity growth, g
A;i
, ^c
i
t+1
=^c
i
t
= e
g
L;i
g
A;i
[ (1 + r
)]
1=
. A steady state in which ^c
i
t+1
= ^c
i
t
in e¢ciency
units is impossible for all countries if population growth rates are heterogeneous. Other steady states are
22

same population growth, suggesting that developing countries catch up with the world pro-
duction frontier mainly through capital deepening. Alternatively, the concept of technology
transfer in McGrattan and Prescott (2009, 2010), and Holmes, McGrattan and Prescott
(2015) represents another appropriate technique for analyzing, e.g., the post-World-War II
transition of southern European economies toward the EU frontier.
In our analysis, the one-child policy in China and its e¤ect on population growth plays the
central role. Since cross-country heterogeneity of population growth is crucial for the present
model, we have used a simple OLG context. For emerging markets, real-world transitional
dynamics which are far from the steady state, can be quite complicated, suggesting that
the assumption of household perfect foresight may be too strong. The myopia (beyond
an adults life span of, e.g., 50-60 years) of an OLG model however, is perhaps the more
appropriate starting point for capturing the rules of thumb used by savers in emerging
economies.
5. Conclusion
The message of our paper is that demographics matter for explaining FDI transitions. It rep-
resents a rst pass at introducing demographics into a formally articulated dynamic model of
FDI. We use the mandatory one-child policy in China, contrasted with Indias comparatively
laissez faire approach as a natural experiment to test for the presence of neoclassical FDI
dynamics. Our evidence and analysis support the hypothesis that neoclassical fundamentals
do govern relative FDI ows.
More broadly, our work is a contribution to the nascent literature on the role of FDI
and technology transfer in international markets in the context of integrated capital mar-
kets (see McGrattan and Prescott, (2009, 2010), and Holmes, McGrattan and Prescott,
impossible, as well.
23
(2015)). Specically, we emphasize the e¤ects of demographic events on FDI ows, a topic
not previously addressed in that literature.
24

6. Appendix A Proof of production aggregation
We omit time subscripts for simplicity. From equations (1), (2), (3), and (14), we obtain,
Y
i
= A
1
i
i
K
i
i
i
L
i
i
1
i
"
1 +
F DI
r
i
K
i
i
i
L
r
i
L
i
i
1
i
#
. (27)
Assuming frictionless cross-country capital ows, condition (7) implies the equlibrium condition:
r
+ = MP K
1
1;t
= MP K
r
1;t
= MP K
2
2;t
= MP K
r
2;t
. (28)
Combining equations (28), (2), and (3), we obtain,
F DI
r
i
L
i
i
= K
i
i
L
r
i
. (29)
Equation (27), combined with (29) and (4) becomes,
Y
i
= A
1
i
i
K
i
i
i
L
i
i
i
L
i
. (30)
Adding the term K
i
i
L
i
i
to both sides of equation (29) leads to (K
i
i
+ F DI
r
i
) L
i
i
= K
i
i
(L
i
i
+ L
r
i
), which implies,
K
i
L
i
=
K
i
i
L
i
i
, (31)
given (4), and given that K
i
= K
i
i
+ F DI
r
i
. Combining (30) with (31) we obtain
Y
i
= A
1
i
i
K
i
L
i
i
L
i
,
which coincides with equation (15), proving the aggregation result.
25

7. Appendix B - Proof of equations (23), (24), and (25)
Equation (22) implies r
+ =
i
K
i
1
i;t
(A
i;t
L
i;t
)
1
i
, which gives,
K
i;t
=
i
r
+
1
1
i
A
i;t
L
i;t
. (32)
Substituting (32) into (15) gives equation (23).
To prove (24), notice that (13) and (15) give,
K
i
i;t+1
= (1 ) K
i
i;t
+
i
(1
i
)
1 +
i
Y
i;t
. (33)
Substituting (33) into (23) implies,
K
i
i;t+1
= (1 ) K
i
i;t
+
i
(1
i
)
1 +
i
i
r
+
i
1
i
A
i;t
L
i;t
. (34)
Dividing both sides of equation (34) by A
i;t
L
i;t
, and considering constant exogenous growth
rates for technology and population, g
A;i
and g
L;i
, we obtain,
e
g
A;i
+g
L;i
K
i
i;t+1
A
i;t+1
L
i;t+1
= (1 )
K
i
i;t
A
i;t
L
i;t
+
i
(1
i
)
1 +
i
i
r
+
i
1
i
. (35)
After placing domestic capital in e¢ciency units, K
i
i;t
= (A
i;t
L
i;t
), on a zero-growth steady-
state path, so that
K
i
i;t
ss
= (A
i;t
L
i;t
) =
K
i
i;t+1
ss
= (A
i;t+1
L
i;t+1
), equation (35) implies,
K
i
i;t
ss
=
i
(1
i
)
(1 +
i
) (e
g
A;i
+g
L;i
+ 1)
i
r
+
i
1
i
A
i;t
L
i;t
| {z }
q
Y
ss
i;t
, (36)
proving equation (24).
For proving equation (25), observe that equation (22) implies,
K
ss
i;t
Y
ss
i;t
=
i
r
+
. (37)
26

Equation (6) together with (37) gives,
K
i
i;t
ss
Y
ss
i;t
+
F DI
r
i;t
ss
Y
ss
i;t
=
i
r
+
. (38)
Equation (36) combined with (23) implies,
K
i
i;t
ss
Y
ss
i;t
=
i
(1
i
)
(1 +
i
) (e
g
A;i
+g
L;i
+ 1)
. (39)
Combining (38) and (39) proves equation (25).
27
REFERENCES
Alfaro, L., S. Kalemli-Ozcan, V. Volosovych (2008): Why Doesnt Capital Flow from
Rich to Poor Countries? An Empirical Investigation, Review of Economics and Sta-
tistics, 90, 347-368.
Azariadis, C. (1996): The Economics of Poverty Traps Part One: Complete Markets,
Journal of Economic Growth, 1, 449-486.
Backus, D. K., P. J. Kehoe, and F. E. Kydland (1992): International Business Cycles,
Journal of Political Economy, 100, 745-775.
Barro, R. J. (1991): Economic Growth in a Cross Section of Countries, Quarterly
Journal of Economics,106, 407-443.
Basu, P. and A. Guariglia (2007): Foreign Direct Investment, inequality, and growth,
Journal of Macroeconomics, 29, 824-839.
Bollard, A., P. Klenow and G. Sharma (2013): Indias mysterious manufacturing mir-
acle, Review of Economic Dynamics, 16, 59-85.
Choukhmane, T., N. Coeurdacier, and K. Jin (2017), The One-Child Policy and House-
hold Saving, mimeo, London School of Economics.
Diamond, P. A. (1965): National Debt in a Neoclassical Growth Model, American
Economic Review, 55, 1126-1150.
De Mello, L. (1997): Foreign direct investment in developing countries and growth: A
selective survey. Journal of Development Studies 34, 1-34.
Du, W., A. Tepper, and A. Verdelhan (2017): Deviations from Covered Interest Rate
Parity, NBER Working Paper 23170.
Durlauf, S., A. Kourtellos, and C. M. Tan (2007): Empirics of Growth and Devel-
opment, International Handbook of Development Economics, A. K. Dutt and J. Ros,
eds., Edward Elgar, Cheltenham, UK.
Gerland, P. et al. (2014): World population stabilization unlikely this century.
Science, 10 October 2014: 346 (6206), 234-237. doiI:10.1126/science.1257469 -
http://www.sciencemag.org/content/346/6206/234.full
Hall, R. E., and C. I. Jones (1999): Why do some countries produce so much more
output per worker than others?, Quarterly Journal of Economics, 114, 83-116.
Holmes, T. J., E. R. McGrattan and E. C. Prescott (2015): Quid Pro Quo: Technology
Capital Transfers for Market Access in China, Review of Economic Studies, 82, 1154
1193.
28
Holston, K., T. Laubach and J. C. Williams (2017): Measuring the natural rate of
interest: International trends and determinants, Journal of International Economics,
108, S59-S75.
Hsieh, C.-T., and P. Klenow (2009): Misallocation and Manufacturing TFP in China
and India, Quarterly Journal of Economics, 124, 1403-1448.
Klenow, P. (1998): Ideas versus rival human capital: Industry evidence on growth
models, Journal of Monetary Economics, 42, 3-23.
Klenow, P., Rodríguez-Clare, A. (1997): The neoclassical revival in growth economics:
has it gone too far?, NBER Macroeconomics Annual, MIT Press, 73-114.
Lucas, R. E. Jr (1990): Why Doesnt Capital Flow from Rich to Poor Countries?,
American Economic Review, Papers and Proceedings, 80, 92-96.
McGrattan. E. R. and E. C. Prescott (2009): Openness, Technology Capital, and
Development, Journal of Economic Theory, 144, 2454-2476.
McGrattan. E. R. and E. C. Prescott (2010): Technology Capital and the US Current
Account, American Economic Review, 1493-1522.
Raftery, A.E., N. Li, H. ev
µ
cíková, P. Gerland, and G.K. Heilig. (2012): Bayesian prob-
abilistic population projections for all countries. Proceedings of the National Academy
of Sciences 109 (35):13915-13921. doi:10.1073/pnas.1211452109
Rosenzweig, M. R., and J. Zhang (2009): Do Population Control Policies Induce More
Human Capital Investment? Twins, Birth Weight and Chinas One-Child Policy,
Review of Economic Studies Limited, 76, 1149-1174.
29

Appendix C - Data Descriptions and Sources
Foreign Direct Investment
1
We use four different data sources to cross-verify the FDI inflows and outflows of China and India.
1. OECD: 1990-2013. Historic time series from OECD FDI statistics to end-2013
(
http://www.oecd.org/daf/inv/investment-policy/fdi-statistics-according-tobmd3.htm).
2. National Accounts: 1982 – 2014. National Bureau of Statistics China (NBS-China) provides FDI
outflow and inflow information (http://data.stats.gov.cn/english/index.htm).
3. UNCTAD (United Nations Conference on Trade and Development): 1981-2013.The UNCTAD work
program on FDI Statistics documents and analyzes global and regional trends in FDI.
4. DataStream: 1981-2016 (Quarterly). Thomson Reuters DataStream provides quarterly data on FDI
inflows and outflows for China and India.
2
Population Estimates and Forecasts: 1950-2100. United Nations: probabilistic population projections based
on the world population prospects (the 2015 revision)
3
.
GDP Series: 1990-2014, 2015-2018 (estimates). Work Bank, PPP adjusted at constant 2011 international
USD.
Capital Stock -GDP ratio (K/Y ratio): PWT 9.0 (The Penn World Table).
FDI data come from four sources: (a) National Accounts, (b) OECD, (c) Datastream, and (d) UNCTAD.
These sources cover different years, so we specify which we use in each context and document the
correlation among these data sources. National account data for India is downloaded from the RBI website
(https://rbi.org.in/Scripts/SDDSView.aspx) and it is identical to the data provided by OECD. So, we only
report the OECD source.
1
All FDI statistics from different sources use 2010 USD as the base dollar value.
2
The quarterly data sources are composed by Oxford Economics (
http://www.oxfordeconomics.com/).
3
United Nations (2015). Probabilistic Population Projections based on the World Population Prospects: The 2015 Revision.
Population Division, DESA. http://esa.un.org/unpd/ppp/.
FDI Inflows – China
Figure A.1
The sources used in the paper are National-account data for the period 1982-2014 and Datastream data for
years 2015-2016. National-account data and Datastream data overlap over the period 1982-2014 with a
correlation coefficient of 99.79%.
FDI Outflows – China
Figure A.2
The sources used in the paper are National-account data for the period 1982-2014 and Datastream data for
years 2015-2016. National-account data and Datastream data overlap over the period 1982-2014 with a
correlation coefficient 99.99%.
100000
300000
Millions in 2010 USD
1980 1990 2000 2010 2016
year
National Account OECD
DataStream UNCTAD
100000
300000
Millions in 2010 USD
1980 1990 2000 2010 2016
year
National Account OECD
DataStream UNCTAD
FDI Inflows - India
Figure A.3
The sources used in the paper are UNCTAD data for the period 1981-2013 and Datastream data for years
2014-2016. UNCTAD data and Datastream data overlap over the period 1981-2013 with a correlation
coefficient of 92.56%. The reason we have chosen UNCTAD data for the period 1981-2013 is because,
(a) for the period between 1981 and 1989 Datastream reports zero values (but not missing values), and
(b) the two data sources overlap over the period 1991-2013 with a correlation coefficient of 99.87%.
FDI Outflows - India
Figure A.4
The sources used in the paper are UNCTAD data for the period 1981-2013 and Datastream data for years
2014-2016. UNCTAD data and Datastream data overlap over the period 1981-2013 with a correlation
coefficient of 89.32%. The reason we have chosen UNCTAD data for the period 1981-2013 is because,
(a) for the period between 1981 and 1993 Datastream reports zero values (but not missing values), and
(b) the two data sources overlap over the period 1994-2013 with a correlation coefficient of 99.86%.
50000
100000
Millions in 2010 USD
1980 1990 2000 2010 2016
year
OECD/National Account
DataStream
UNCTAD
50000
100000
Millions in 2010 USD
1980 1990 2000 2010 2016
year
OECD/National Account
DataStream
UNCTAD
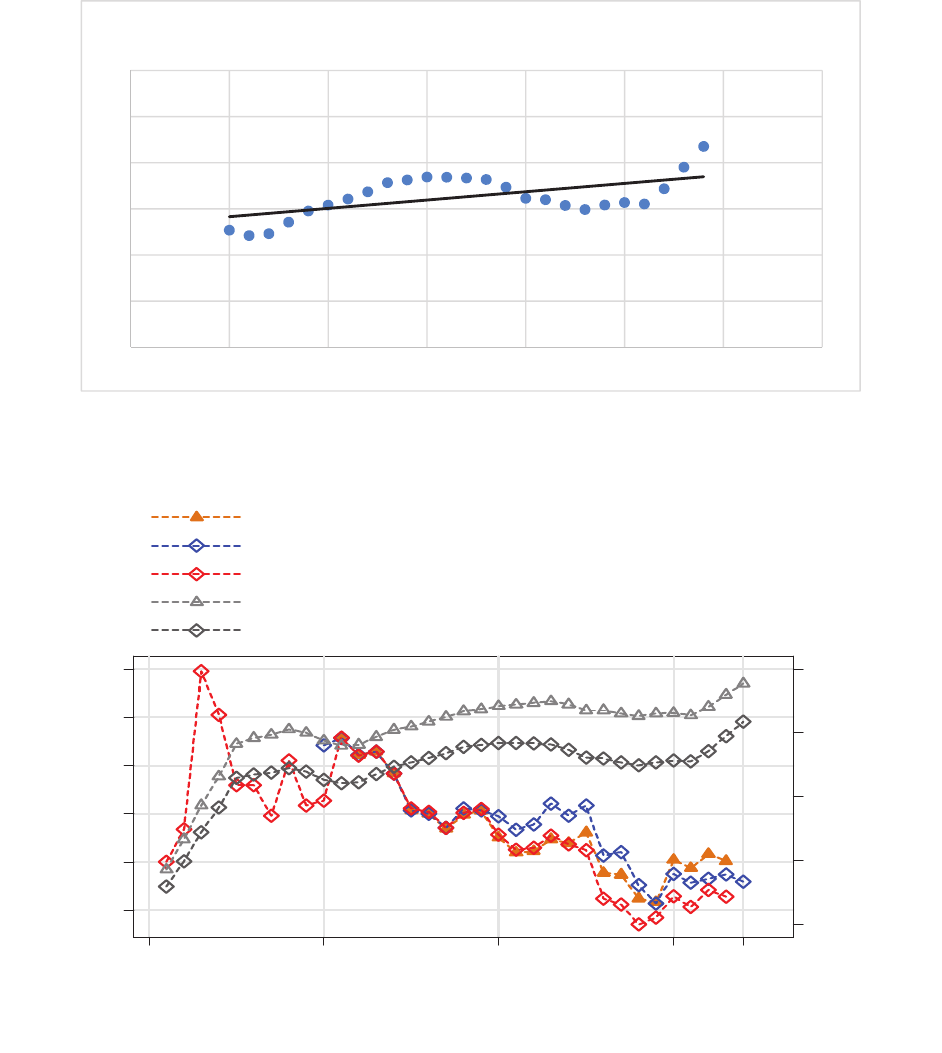
Figure A.5
Figure A.6
To address the concern that large-scale internal migration in China would decrease the capital-labor ratio
instead of increasing it, we use the urban population, restricted to ages 15-64 and perform a robustness
check. Figure A.5 shows that the linear time trend coefficient (of the log K/L ratio of China over the K/L
ratio of India) is positive and statistically significant (not equal to 0 with p-value at 0.3%). In Figure A.6
where we plot a similar data series as Figure 5 (in the paper) using this restricted sample, all the quantitative
results remain.
y= Ͳ 6.8932+0.0036*Time
(tͲstat=3.39,Pvalue=0.3%)
0
0.1
0.2
0.3
0.4
0.5
0.6
1985 1990 1995 2000 2005 2010 2015 2020
Log(DiffKͲLRatioUrbanLaborForce)
-.2
0
.2
.4
.6
log[(KLratio-CN)/(KLratio-IN)]
0
1
2
3
4
5
log[(FDIinflow-CN/GDP-CN)/(FDIinflow-IN/GDP-IN)]
1980 1990 2000 2010 2014
year
OECD/NationalAccount - Left axis
DataStream - Left axis
UNCTAD - Left axis
PennWT, WorldBank - Right axis (urban pop - all)
PennWT, WorldBank - Right axis (urban pop - age 15-64 )
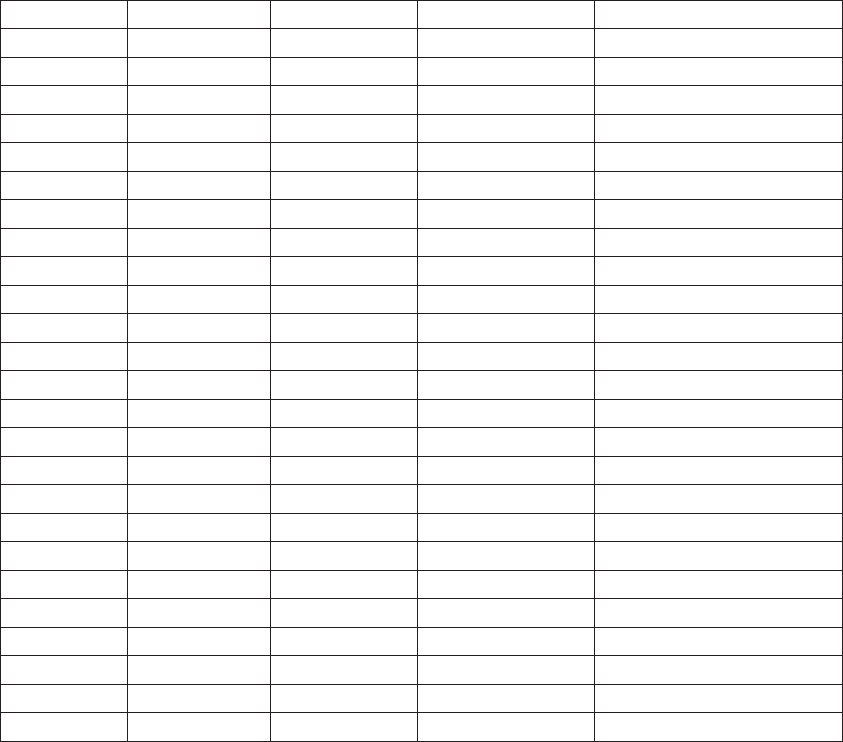
The first two columns of Table A.1 provide the data appearing in Figure A.6 (without the logarithmic
conversion of ratios). The last two columns of Table A.1 are the two new urban (working) population series
appearing in Figure A.6.
year Ratio_FDIY Ratio_FullPop Ratio_PopUrban Ratio_PopUrbanWorking
1990 30.45 0.96 1.46 1.29
1991 35.73 0.99 1.43 1.27
1992 25.08 1.02 1.44 1.28
1993 26.94 1.07 1.47 1.31
1994 17.04 1.13 1.51 1.34
1995 7.96 1.17 1.52 1.36
1996 7.42 1.22 1.55 1.38
1997 5.54 1.27 1.57 1.40
1998 8.32 1.32 1.60 1.43
1999 7.95 1.36 1.61 1.44
2000 7.02 1.41 1.62 1.45
2001 5.33 1.50 1.63 1.45
2002 5.94 1.57 1.64 1.44
2003 9.19 1.66 1.65 1.44
2004 7.14 1.73 1.63 1.41
2005 8.79 1.72 1.60 1.38
2006 3.11 1.72 1.60 1.38
2007 3.36 1.71 1.59 1.36
2008 1.69 1.68 1.57 1.35
2009 1.16 1.70 1.59 1.36
2010 2.12 1.72 1.59 1.37
2011 1.77 1.72 1.58 1.36
2012 1.92 1.77 1.62 1.41
2013 2.11 1.87 1.68 1.48
2014 1.81 1.97 1.74 1.55
Table A.1
